2024年中考数学考前20天终极冲刺专题之测量类应用
试卷更新日期:2024-05-22 类型:三轮冲刺
一、选择题
-
1. 如图,将一个形状的楔子从木桩的底端点P沿水平方向打入木桩底下,可以使木桩向上运动.若楔子斜面的倾斜角为 , 楔子沿水平方向前进5厘米,则木桩上升( )
 A、厘米 B、厘米 C、厘米 D、厘米2. 如图,在平地上种植树木时,要求株距(相邻两棵树之间的水平距离)为5m , 若在坡比为i=1:2.5的山坡种树,也要求株距为5m , 那么相邻两棵树间的坡面距离为( )
A、厘米 B、厘米 C、厘米 D、厘米2. 如图,在平地上种植树木时,要求株距(相邻两棵树之间的水平距离)为5m , 若在坡比为i=1:2.5的山坡种树,也要求株距为5m , 那么相邻两棵树间的坡面距离为( ) A、2.5m B、5m C、 D、10m3. 如图,天定山滑雪场有一坡角为的滑雪道,滑雪道长为150米,则滑雪道的坡顶到坡底的竖直高度的长为( )
A、2.5m B、5m C、 D、10m3. 如图,天定山滑雪场有一坡角为的滑雪道,滑雪道长为150米,则滑雪道的坡顶到坡底的竖直高度的长为( ) A、米 B、米 C、米 D、米4. 一配电房示意图如图所示, 它是一个轴对称图形. 已知 , , 则房顶 离地面 的高度为( )
A、米 B、米 C、米 D、米4. 一配电房示意图如图所示, 它是一个轴对称图形. 已知 , , 则房顶 离地面 的高度为( ) A、 B、 C、 D、5. 如图①, 将一个楔子Rt 从木桩的底端点 沿水平方向打入木桩底下, 使木桩向上运动. 如果楔子斜面的倾斜角为 , 楔子沿水平方向前进 (如图②), 那么木桩上升的高度为( )
A、 B、 C、 D、5. 如图①, 将一个楔子Rt 从木桩的底端点 沿水平方向打入木桩底下, 使木桩向上运动. 如果楔子斜面的倾斜角为 , 楔子沿水平方向前进 (如图②), 那么木桩上升的高度为( ) A、 B、 C、 D、6. 如图是一款桌面可调整的学习桌,桌面宽度AB为60cm,桌面平放时高度DE为70cm,若书写时桌面适宜倾斜角的度数为 , 则桌沿(点A)处到地面的高度h为( )
A、 B、 C、 D、6. 如图是一款桌面可调整的学习桌,桌面宽度AB为60cm,桌面平放时高度DE为70cm,若书写时桌面适宜倾斜角的度数为 , 则桌沿(点A)处到地面的高度h为( )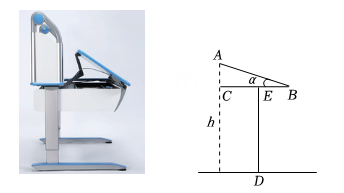
A、 B、 C、 D、7. 某路灯示意图如图所示,它是轴对称图形,若∠ACB=130°,AC=BC=1.2m,CD 与地面垂直且CD=6m,则灯顶 A 到地面的高度为( ) A、 B、 C、 D、8. “圭表”是中国古代用来确定节气的仪器.某“圭表”示意图如图所示, , 米,测得某地夏至正午时“表”的影长米,冬至时的正午太阳高度角 , 则夏至到冬至,影长差的长为( )
A、 B、 C、 D、8. “圭表”是中国古代用来确定节气的仪器.某“圭表”示意图如图所示, , 米,测得某地夏至正午时“表”的影长米,冬至时的正午太阳高度角 , 则夏至到冬至,影长差的长为( ) A、米 B、米 C、米 D、米9. 榫卯是古代中国建筑、家具及其他器械的主要结构方式.如图,在某燕尾榫中,榫槽的横截面是梯形,其中 , , 燕尾角 , 外口宽 , 榫槽深度是 , 则它的里口宽为( )
A、米 B、米 C、米 D、米9. 榫卯是古代中国建筑、家具及其他器械的主要结构方式.如图,在某燕尾榫中,榫槽的横截面是梯形,其中 , , 燕尾角 , 外口宽 , 榫槽深度是 , 则它的里口宽为( )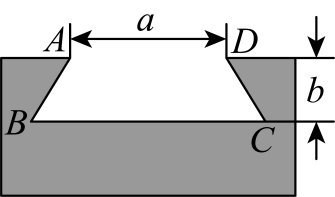 A、 B、 C、 D、10. 日照灯塔是日照海滨港口城市的标志性建筑之一,主要为日照近海及进出日照港的船舶提供导航服务.数学小组的同学要测量灯塔的高度,如图所示,在点B处测得灯塔最高点A的仰角 , 再沿方向前进至C处测得最高点A的仰角 , , 则灯塔的高度大约是( )(结果精确到 , 参考数据: , )
A、 B、 C、 D、10. 日照灯塔是日照海滨港口城市的标志性建筑之一,主要为日照近海及进出日照港的船舶提供导航服务.数学小组的同学要测量灯塔的高度,如图所示,在点B处测得灯塔最高点A的仰角 , 再沿方向前进至C处测得最高点A的仰角 , , 则灯塔的高度大约是( )(结果精确到 , 参考数据: , ) A、 B、 C、 D、11. 一个水杯竖直放置时的纵向截面如图1所示,其左右轮廓线AC,BD都是同一条抛物线的一部分,AB,CD都与水面桌面平行,已知水杯底部AB宽为4cm,水杯高度为12cm,当水面高度为6cm时,水面宽度为2cm.如图2先把水杯盛满水,再将水杯绕A点倾斜倒出部分水,如图3,当倾斜角∠BAF=30°时,杯中水面CE平行水平桌面AF.则此时水面CE的值是( )
A、 B、 C、 D、11. 一个水杯竖直放置时的纵向截面如图1所示,其左右轮廓线AC,BD都是同一条抛物线的一部分,AB,CD都与水面桌面平行,已知水杯底部AB宽为4cm,水杯高度为12cm,当水面高度为6cm时,水面宽度为2cm.如图2先把水杯盛满水,再将水杯绕A点倾斜倒出部分水,如图3,当倾斜角∠BAF=30°时,杯中水面CE平行水平桌面AF.则此时水面CE的值是( )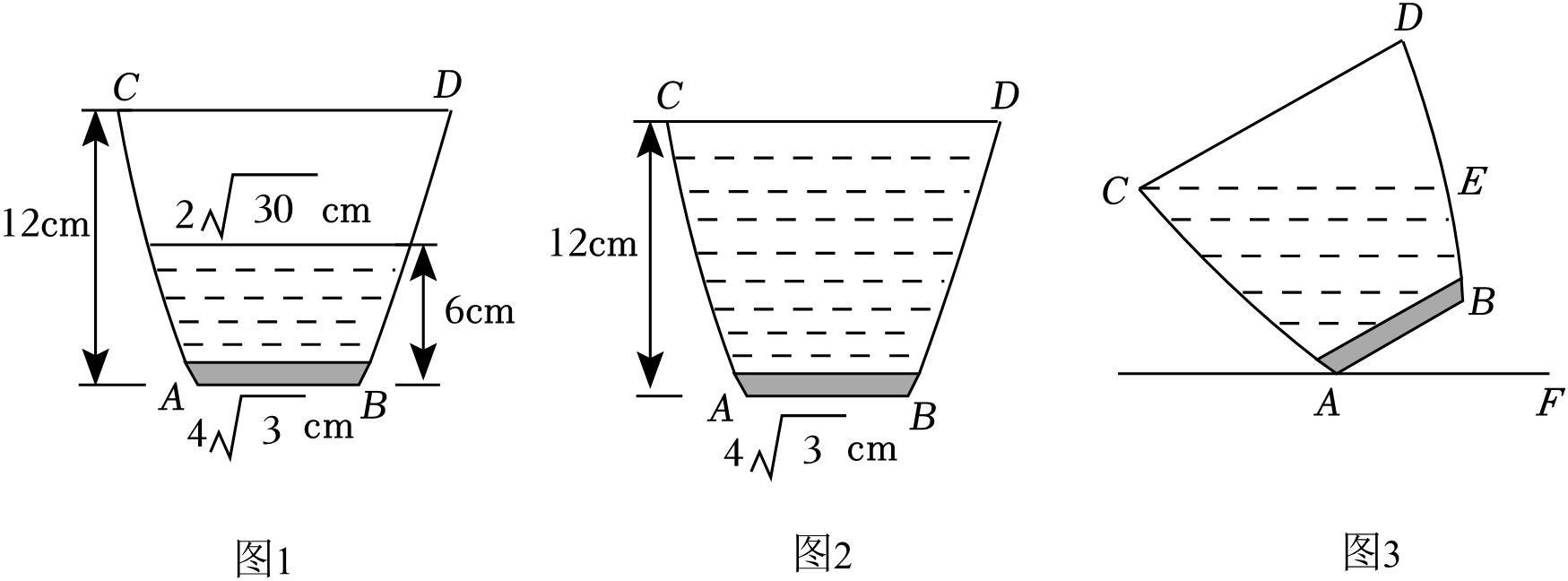 A、 B、12cm C、 D、14cm
A、 B、12cm C、 D、14cm二、填空题
-
12. 如图,ED 为一条宽为 的河, 河的西岸建有一道防洪堤, 防洪堤与东岸的高度差为 (即 ). 因为施工需要, 现准备将东岸的泥沙通过滑轨送到西岸的防洪堤上, 防洪堤上已经建好一座固定滑轨一端的钢架, 现准备在东岸找一个点 作为另一端的固定点. 已知吊篮的截面为直径为 的半圆 (直径 ), 绳子 , 钢架高度为 , 距离防洪堤边缘为 .
 (1)、 西岸边缘点 与东岸边缘点 之间的距离为 .(2)、滑轨在运送货物时保持笔直, 要想做到运输过程中吊篮一定不会碰到点 , 则 的长应大于 .13. 阅读材料:在中, , , 求的值.
(1)、 西岸边缘点 与东岸边缘点 之间的距离为 .(2)、滑轨在运送货物时保持笔直, 要想做到运输过程中吊篮一定不会碰到点 , 则 的长应大于 .13. 阅读材料:在中, , , 求的值.解题思路:在上截取 , 再连接 , 可证为等腰三角形,设 , 则 , 则 , .
 14. 图1是一种儿童可折叠滑板车,该滑板车完全展开后示意图如图2所示,由车架和两个大小相同的车轮组成,已知 , 当在同一水平高度上时, , 则;为方便存放,将车架前部分绕着点旋转至 , 如图3所示,则为 .
14. 图1是一种儿童可折叠滑板车,该滑板车完全展开后示意图如图2所示,由车架和两个大小相同的车轮组成,已知 , 当在同一水平高度上时, , 则;为方便存放,将车架前部分绕着点旋转至 , 如图3所示,则为 .
三、解答题
-
15. 某校学生利用课余时间,使用卷尺和测角仪测量某公园古城门的高度.如图所示,他们先在公园广场点M处架设测角仪,测得古城门最高点A的仰角为22°,然后前进20m到达点N处,测得点A的仰角为45°;已知测角仪的高度为1.4m . 求古城门最高点A距离地面的高度.(结果精确到0.1m;参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
 16. 筒车是我国古代利用水力驱动的灌溉工具,如图,半径为3m的筒车⊙O按逆时针方向每分钟转圈,筒车与水面分别交于点A、B , 筒车的轴心O距离水面的高度OC为2.2m , 筒车上均匀分布着若干个盛水筒,若以某个盛水筒P刚浮出水面(点A)时开始计算时间.
16. 筒车是我国古代利用水力驱动的灌溉工具,如图,半径为3m的筒车⊙O按逆时针方向每分钟转圈,筒车与水面分别交于点A、B , 筒车的轴心O距离水面的高度OC为2.2m , 筒车上均匀分布着若干个盛水筒,若以某个盛水筒P刚浮出水面(点A)时开始计算时间. (1)、求盛水筒P从A点到达最高点所经过的路程;(2)、求浮出水面3.4秒时,盛水筒P到水面的距离;(3)、若接水槽MN所在直线是⊙O的切线,且与直线AB交于点M , MO=8m , 直接写出盛水筒P从最高点开始,经过多长时间恰好第一次落在直线MN上.(参考数据:cos43°=sin47°≈ , sin16°=cos74°≈ , sin22°=cos68°≈)17. 某校组织九年级学生参加社会实践活动,数学学科的项目任务是测量银山塔林中某塔的高度 , 其中一个数学兴趣小组设计的方案如图所示,他们在点C处用高1.5m的测角仪测得塔顶A的仰角为 , 然后沿方向前行7m到达点F处,在F处测得塔顶A的仰角为 . 请根据他们的测量数据求塔高的长度大约是多少.(参考数据: , , , , , . )
(1)、求盛水筒P从A点到达最高点所经过的路程;(2)、求浮出水面3.4秒时,盛水筒P到水面的距离;(3)、若接水槽MN所在直线是⊙O的切线,且与直线AB交于点M , MO=8m , 直接写出盛水筒P从最高点开始,经过多长时间恰好第一次落在直线MN上.(参考数据:cos43°=sin47°≈ , sin16°=cos74°≈ , sin22°=cos68°≈)17. 某校组织九年级学生参加社会实践活动,数学学科的项目任务是测量银山塔林中某塔的高度 , 其中一个数学兴趣小组设计的方案如图所示,他们在点C处用高1.5m的测角仪测得塔顶A的仰角为 , 然后沿方向前行7m到达点F处,在F处测得塔顶A的仰角为 . 请根据他们的测量数据求塔高的长度大约是多少.(参考数据: , , , , , . )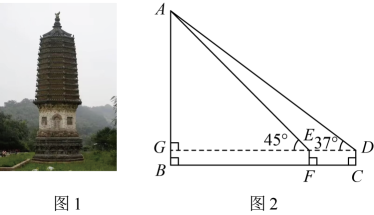 18. 嵩岳寺塔,位于登封市区西北5公里嵩山南麓峻极峰下嵩岳寺内,是嵩岳寺内唯一的北魏遗存建筑,也是中国现存最古老的砖塔,它见证了这座寺院的千年历史.小明想知道塔的高度.于是走到点C处,测得此时塔尖A的仰角是37°,向前走了11.8米至点F处,测得此时塔尖A的仰角是45°,已知小明的眼睛离地面高度是1.6米,请你帮他求出嵩岳寺塔AB的高度.(参考数据:sin37°≈ , cos37°≈ , tan37°≈)
18. 嵩岳寺塔,位于登封市区西北5公里嵩山南麓峻极峰下嵩岳寺内,是嵩岳寺内唯一的北魏遗存建筑,也是中国现存最古老的砖塔,它见证了这座寺院的千年历史.小明想知道塔的高度.于是走到点C处,测得此时塔尖A的仰角是37°,向前走了11.8米至点F处,测得此时塔尖A的仰角是45°,已知小明的眼睛离地面高度是1.6米,请你帮他求出嵩岳寺塔AB的高度.(参考数据:sin37°≈ , cos37°≈ , tan37°≈)
四、实践探究题
-
19. 某综合实践研究小组为了测量观察目标时的仰角和俯角, 利用量角器和铅锤自制了一个简易测角仪, 如图①所示.
 (1)、 如图 ②, 在点 观察所测物体最高点 , 当量角器零刻度线上 两点均在视线 上时,测得视线与铅垂线所夹的锐角为 , 设仰角为 , 请直接用含 的代数式表示 .(2)、 如图③, 为了测量广场上空气球 离地面的高度,该小组利用自制简易测角仪在点 分别测得气球 的仰角 为 为 , 地面上点 在同一水平直线上, , 求气球 离地面的高度 .
(1)、 如图 ②, 在点 观察所测物体最高点 , 当量角器零刻度线上 两点均在视线 上时,测得视线与铅垂线所夹的锐角为 , 设仰角为 , 请直接用含 的代数式表示 .(2)、 如图③, 为了测量广场上空气球 离地面的高度,该小组利用自制简易测角仪在点 分别测得气球 的仰角 为 为 , 地面上点 在同一水平直线上, , 求气球 离地面的高度 .(参考数据:
20. 问题: 如何设计“倍力桥”的结构?图 38-1①是搭成的 “倍力桥”, 纵梁 夹住横梁 , 使得横梁不能移动, 结构稳固.
图 38-1②是长为 , 宽为 的横梁侧面示意图, 三个凹槽都是半径为 的半圆, 圆心分别为 , 纵梁是底面半径为 的圆柱体, 用相同规格的横梁、纵梁搭“桥”,间隙忽略不计.
 (1)、探究 1: 图 38-1③是 “桥”侧面示意图, 为横梁与地面的交点, 为圆心, , 是横梁侧面两边的交点, 测得 , 点 到 的距离为 , 试判断四边形 的形状,并求 的值.(2)、探究 2: 若搭成的“桥”刚好能绕成环,其侧面示意图的内部形成一个多边形.
(1)、探究 1: 图 38-1③是 “桥”侧面示意图, 为横梁与地面的交点, 为圆心, , 是横梁侧面两边的交点, 测得 , 点 到 的距离为 , 试判断四边形 的形状,并求 的值.(2)、探究 2: 若搭成的“桥”刚好能绕成环,其侧面示意图的内部形成一个多边形.①若有 12 根横梁绕成环, 图 38-1④是其侧面示意图, 内部形成十二边形 , 求 的值.
②若有 根横梁绕成的环 ( 为偶数, 且 , 试用关于 的代数式表示内部形成的多边形 的周长.
21. 一透明的敞口正方体容器ABCD﹣A'B'C'D'装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α(∠CBE=α,如图所示).

探究:如图1,液面刚好过棱CD , 并与棱BB'交于点Q , 此时液体的形状为直三棱柱,其三视图及尺寸如图②.
(1)、解决问题:CQ与BE的位置关系是 , BQ的长是dm , α=°(注:sin49°=cos41° , tan37°)(2)、求液体的体积;(参考算法:直棱柱体积V液=底面积SBCQ×高AB)(3)、在图1的基础上,以棱AB为轴将容器向左或向右旋转,但不能使液体溢出.图3或图4是其正面示意图,若液面与棱C'C或CB交于点P、点Q始终在棱BB'上,设PC=x , BQ=y , 分别就图3和图4求y与x的函数关系式,并写出相应的α的范围.22. 【阅读理解】:如图,在中,a,b,c分别是 , , 的对边, , 其外接圆半径为R.根据锐角三角函数的定义: , , 可得 , 即(规定). (1)、【探究活动】:如图,在锐角中,a,b,c分别是 , , 的对边,其外接圆半径为R,那么:(用>,=或<连接),并说明理由 .
(1)、【探究活动】:如图,在锐角中,a,b,c分别是 , , 的对边,其外接圆半径为R,那么:(用>,=或<连接),并说明理由 .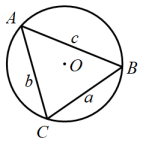 (2)、【初步应用】:事实上,以上结论适用于任意三角形.在中,a,b,c分别是 , , 的对边.已知 , , , 求 .(3)、【综合应用】:如图,在某次数学实践活动中,小莹同学测量一栋楼的高度,在A处用测角仪测得地面点C处的俯角为45°,点D处的俯角为15°,B,C,D在一条直线上,且C,D两点的距离为100m,求楼的高度.(参考数据: , )
(2)、【初步应用】:事实上,以上结论适用于任意三角形.在中,a,b,c分别是 , , 的对边.已知 , , , 求 .(3)、【综合应用】:如图,在某次数学实践活动中,小莹同学测量一栋楼的高度,在A处用测角仪测得地面点C处的俯角为45°,点D处的俯角为15°,B,C,D在一条直线上,且C,D两点的距离为100m,求楼的高度.(参考数据: , )