2024年中考数学考前20天终极冲刺专题之尺规作图(一)
试卷更新日期:2024-05-22 类型:三轮冲刺
一、选择题
-
1. 如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:
①作线段AB , 分别以A , B为圆心,以AB长为半径作弧,两弧的交点为C;
②以点C为圆心,仍以AB长为半径作弧交AC的延长线于点D;
③连结BD、BC . 则下列说法不正确的是( )
 A、△ABC是正三角形 B、∠CBD=30° C、点C在BD的中垂线上 D、cosD=2. 如图,已知线段a , h作等腰△ABC , 使AB=AC , 且BC=a , BC边上的高AD=h . 张红的作法如下:
A、△ABC是正三角形 B、∠CBD=30° C、点C在BD的中垂线上 D、cosD=2. 如图,已知线段a , h作等腰△ABC , 使AB=AC , 且BC=a , BC边上的高AD=h . 张红的作法如下:
作线段BC=a;
作线段BC的垂直平分线MN , MN与BC相交于点D;
在直线MN上截取线段h;
连结AB , AC , 则△ABC为所求的等腰三角形.
上述作法的四个步骤中,有错误的一步你认为是( )
A、 B、 C、 D、3. 在中, , . 用无刻度的直尺和圆规在内部作一个角 , 下列作法中不等于的是( )A、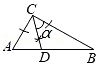 B、
B、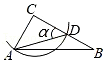 C、
C、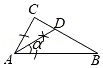 D、
D、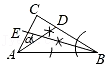 4. 如图,下列四种用无刻度直尺和圆规作角平分线的方法,其中不正确的个数是( )
4. 如图,下列四种用无刻度直尺和圆规作角平分线的方法,其中不正确的个数是( ) A、个 B、个 C、个 D、个5. 用尺规作图作三角形的外接圆时,用到了哪些基本作图( )A、作一条线段等于已知线段 B、作一个角等于已知角 C、作一个角的平分线 D、作一条线段的垂直平分线6. 如图,Rt△ABC中,∠C=90°,用尺规分别截取BE , BD , 使BE=BD , 分别以D、E为圆心、以大于 的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G . 若CG=1,P为AB上一动点,则GP的最小值为( )
A、个 B、个 C、个 D、个5. 用尺规作图作三角形的外接圆时,用到了哪些基本作图( )A、作一条线段等于已知线段 B、作一个角等于已知角 C、作一个角的平分线 D、作一条线段的垂直平分线6. 如图,Rt△ABC中,∠C=90°,用尺规分别截取BE , BD , 使BE=BD , 分别以D、E为圆心、以大于 的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G . 若CG=1,P为AB上一动点,则GP的最小值为( ) A、无法确定 B、 C、1 D、2
A、无法确定 B、 C、1 D、2二、填空题
-
7. 如图,在中, , , 进行如下操作:①以点为圆心,以小于长为半径作弧,分别交、于点、;②分别以、为圆心,以大于长为半径作弧,两弧交于点;③作射线交于点 , 则的度数为 .
 8. 如图,线段 ,用尺规作图法按如下步骤作图.
8. 如图,线段 ,用尺规作图法按如下步骤作图.
①过点B作 的垂线,并在垂线上取 ;
②连接 ,以点C为圆心, 为半径画弧,交 于点E;
③以点A为圆心, 为半径画弧,交 于点D . 即点D为线段 的黄金分割点.
则线段 的长度约为 (结果保留两位小数,参考数据: )
三、作图题
-
9. 如图,平行四边形ABCD中,AE=CE , 请仅用无刻度的直尺完成下列作图:
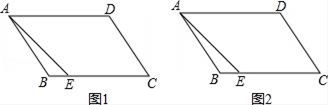 (1)、在图1中,作出∠DAE的角平分线;(2)、在图2中,作出∠AEC的角平分线.10. 如图,已知ABCD .
(1)、在图1中,作出∠DAE的角平分线;(2)、在图2中,作出∠AEC的角平分线.10. 如图,已知ABCD . (1)、尺规作图:延长BC并在BC的延长线上截取线段CE , 使得 (保留作图痕迹,不要求写作法);(2)、在(1)的条件下,连结AE , 交CD于点F , 求证: .11. 工人师傅在裁剪直角三角材料时通常采用“三弧法”:①画线段AB,分别以A、B为圆心,AB长为半径画弧,相交于点C;②以C为圆心,仍以AB长为半径画弧,交AC的延长线于D;③连接DB,则△ABD为直角三角形.请完成下列问题:(1)、按工人师傅的画法作图(保留作图痕迹);(2)、证明:△ABD为直角三角形.12. 如图,按下列要求图:(要求有明显的作图痕迹,不写作法)
(1)、尺规作图:延长BC并在BC的延长线上截取线段CE , 使得 (保留作图痕迹,不要求写作法);(2)、在(1)的条件下,连结AE , 交CD于点F , 求证: .11. 工人师傅在裁剪直角三角材料时通常采用“三弧法”:①画线段AB,分别以A、B为圆心,AB长为半径画弧,相交于点C;②以C为圆心,仍以AB长为半径画弧,交AC的延长线于D;③连接DB,则△ABD为直角三角形.请完成下列问题:(1)、按工人师傅的画法作图(保留作图痕迹);(2)、证明:△ABD为直角三角形.12. 如图,按下列要求图:(要求有明显的作图痕迹,不写作法) (1)、作出的角平分线CD;(2)、作出的中线BE;(3)、作出的高BG.13. 如图所示,已知在△ABC中,∠A=90°.
(1)、作出的角平分线CD;(2)、作出的中线BE;(3)、作出的高BG.13. 如图所示,已知在△ABC中,∠A=90°. (1)、请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明).(2)、若∠ABC=60,AB=3,求⊙P的面积.14. 尺规作图
(1)、请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明).(2)、若∠ABC=60,AB=3,求⊙P的面积.14. 尺规作图如图,某地有两个小区A,B和两条相交的供水管道OC,OD.现计划在S区域内修建一个蓄水池,要求到两个小区的距离相等,到两条公路的距离也相等,请确定蓄水池的位置.(保留作图痕迹,不写作法)
 15. 如图,□ABCD 的顶点A、B、D都在⊙O上,请你仅用无刻度的直尺按下列要求画图:
15. 如图,□ABCD 的顶点A、B、D都在⊙O上,请你仅用无刻度的直尺按下列要求画图: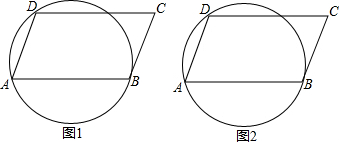 (1)、在图1中,画出一条弦与AD相等;(2)、在图2中,画出一条直线与AB垂直平分.16. 已知 , 是的两条切线,切点分别是、B,BC垂直于C,请只用无刻度直尺,按要求画图,保留作图痕迹.
(1)、在图1中,画出一条弦与AD相等;(2)、在图2中,画出一条直线与AB垂直平分.16. 已知 , 是的两条切线,切点分别是、B,BC垂直于C,请只用无刻度直尺,按要求画图,保留作图痕迹. (1)、如图1,连接 , 并作出线段的中点;(2)、如图2,连接 , 过点A作线段AE平行交PB于点E.17. 图①、图②、图③均为3×5的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,按下列要求作图:
(1)、如图1,连接 , 并作出线段的中点;(2)、如图2,连接 , 过点A作线段AE平行交PB于点E.17. 图①、图②、图③均为3×5的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,按下列要求作图: (1)、在图①中,连结AC、BC,使AC=AB,∠BAC=90°;(2)、在图②中,连结AC、BC,使AC=BC,∠ACB=90°;(3)、在图③中,连结AC、BC,使AC=BC,∠ACB≠90°18. 如图,点A、B、C在8×5网格的格点上,每小方格是边长为1个单位长度的正方形.请按要求画图,并回答问题:
(1)、在图①中,连结AC、BC,使AC=AB,∠BAC=90°;(2)、在图②中,连结AC、BC,使AC=BC,∠ACB=90°;(3)、在图③中,连结AC、BC,使AC=BC,∠ACB≠90°18. 如图,点A、B、C在8×5网格的格点上,每小方格是边长为1个单位长度的正方形.请按要求画图,并回答问题: (1)、①延长线段AB到点D,使BD=AB;
(1)、①延长线段AB到点D,使BD=AB;②过点C画CE⊥AB,垂足为E;
(2)、点C到直线AB的距离是个单位长度;(3)、通过测量= , 并由此结论可猜想直线BC与AF的位置关系是 .19. 如图,在6×6的方格纸中,每个小正方形的顶点称为格点,每个小正方形的边长均为1,A,B两点均在格点上.请按要求在图①,图②,图③中画图: (1)、在图①中,画等腰△ABC,使AB为腰,点C在格点上.(2)、在图②中,画面积为8的四边形ABCD,使其为中心对称图形,但不是轴对称图形,C,D两点均在格点上.(3)、在图③中,画△ABC,使∠ACB=90°,面积为5,点C在格点上.20. 如图,在5×5的正方形网格中有一条线段AB , 点A、B都在格点上.
(1)、在图①中,画等腰△ABC,使AB为腰,点C在格点上.(2)、在图②中,画面积为8的四边形ABCD,使其为中心对称图形,但不是轴对称图形,C,D两点均在格点上.(3)、在图③中,画△ABC,使∠ACB=90°,面积为5,点C在格点上.20. 如图,在5×5的正方形网格中有一条线段AB , 点A、B都在格点上.

 (1)、在图①中以AB为边,画出一个是轴对称,但不是中心对称的四边形ABCD , C、D为格点.(2)、在图②中以AB为边,画出一个是中心对称,但不是轴对称的四边形ABCD , C、D为格点.(3)、在图③中以AB为边,画出一个既是中心对称,又是轴对称的四边形ABCD , C、D为格点.21. 如图,在正方形网格中每个小正方形的边长为1,小正方形的顶点称为格点,在正方形网格中分别画出下列图形:
(1)、在图①中以AB为边,画出一个是轴对称,但不是中心对称的四边形ABCD , C、D为格点.(2)、在图②中以AB为边,画出一个是中心对称,但不是轴对称的四边形ABCD , C、D为格点.(3)、在图③中以AB为边,画出一个既是中心对称,又是轴对称的四边形ABCD , C、D为格点.21. 如图,在正方形网格中每个小正方形的边长为1,小正方形的顶点称为格点,在正方形网格中分别画出下列图形: (1)、在图(1)网格中画出长为 的线段AB.(2)、在图(2)网格中画出一个腰长为 ,面积为3的等腰22. 图①、图②、图③均是 的正方形网格,每个小正方形的边长均为1.每个小正方形的顶点称为格点,点A、B、C均为格点,只用无刻度的直尺,分别在给定的网格中找一格点M , 按下列要求作图:
(1)、在图(1)网格中画出长为 的线段AB.(2)、在图(2)网格中画出一个腰长为 ,面积为3的等腰22. 图①、图②、图③均是 的正方形网格,每个小正方形的边长均为1.每个小正方形的顶点称为格点,点A、B、C均为格点,只用无刻度的直尺,分别在给定的网格中找一格点M , 按下列要求作图: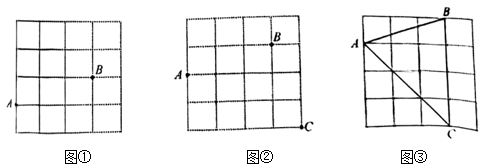 (1)、在图①中,连结MA、MB , 使 .(2)、在图②中,连结MA、MB、MC , 使 .(3)、在图③中,连结MA、MC , 使 .23. 在每个小正方形的边长为 的网格中,点 , 在格点上.请用无刻度的直尺,按下列要求画图.
(1)、在图①中,连结MA、MB , 使 .(2)、在图②中,连结MA、MB、MC , 使 .(3)、在图③中,连结MA、MC , 使 .23. 在每个小正方形的边长为 的网格中,点 , 在格点上.请用无刻度的直尺,按下列要求画图. (1)、在图①画出一个以 为一边的正方形 ;(2)、在图②画出一个以 为一边的菱形 ( 不是正方形);(3)、如图③,点 , 在格点上, 与 交于点 ,在图③中画出一个以 为一边的矩形 .24. 如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)、在图①画出一个以 为一边的正方形 ;(2)、在图②画出一个以 为一边的菱形 ( 不是正方形);(3)、如图③,点 , 在格点上, 与 交于点 ,在图③中画出一个以 为一边的矩形 .24. 如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形. (1)、在图1中,画一个三角形,使它的三边长都是有理数;(2)、在图2中,画一个正方形,使它的面积是10.
(1)、在图1中,画一个三角形,使它的三边长都是有理数;(2)、在图2中,画一个正方形,使它的面积是10.

