2024年中考数学考前20天终极冲刺专题之旋转问题
试卷更新日期:2024-05-22 类型:三轮冲刺
一、选择题
-
1. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,在△ABC中,AB<AC,将△ABC以点A为旋转中心逆时针旋转得到△ADE,点D在BC边上,DE交AC于点F,则下列结论中错误的是( )
2. 如图,在△ABC中,AB<AC,将△ABC以点A为旋转中心逆时针旋转得到△ADE,点D在BC边上,DE交AC于点F,则下列结论中错误的是( ) A、△AFE∽△DFC B、AD=AF C、DA平分∠BDE D、∠CDF=∠BAD3. 如图,已知是矩形的对角线,以点为旋转中心将逆时针旋转 , 得到 , , , 三点恰好在同一条直线上,设与相交于点 , 连结有以下结论:;∽;是线段的黄金分割点;其中正确的是( )
A、△AFE∽△DFC B、AD=AF C、DA平分∠BDE D、∠CDF=∠BAD3. 如图,已知是矩形的对角线,以点为旋转中心将逆时针旋转 , 得到 , , , 三点恰好在同一条直线上,设与相交于点 , 连结有以下结论:;∽;是线段的黄金分割点;其中正确的是( ) A、 B、 C、 D、4. 如图,在△ABC中,∠ACB=105°,将△ABC绕着点C顺时针方向旋转到△ , 经过点 A . 若=AC , 则∠B的度数为( )
A、 B、 C、 D、4. 如图,在△ABC中,∠ACB=105°,将△ABC绕着点C顺时针方向旋转到△ , 经过点 A . 若=AC , 则∠B的度数为( ) A、20° B、25° C、30° D、35°5. 如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=4,BD=6,则CD的长为( )
A、20° B、25° C、30° D、35°5. 如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=4,BD=6,则CD的长为( ) A、3 B、4 C、2 D、26. 如图,把以点A为中心逆时针旋转得到 , 点B,C的对应点分别是点D,E,且点E在的延长线上,连接 , 则下列结论一定正确的是( )
A、3 B、4 C、2 D、26. 如图,把以点A为中心逆时针旋转得到 , 点B,C的对应点分别是点D,E,且点E在的延长线上,连接 , 则下列结论一定正确的是( )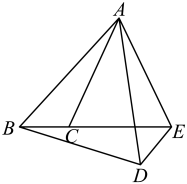 A、 B、 C、 D、7. 如图,中, , 将绕点顺时针旋转得到 , 使点的对应点恰好落在边上,、交于点 . 若 , 则的度数是( )(用含的代数式表示)
A、 B、 C、 D、7. 如图,中, , 将绕点顺时针旋转得到 , 使点的对应点恰好落在边上,、交于点 . 若 , 则的度数是( )(用含的代数式表示) A、 B、 C、 D、8. 如图,将矩形绕点顺时针旋转到矩形的位置,旋转角为 . 若 , 则的大小是( )
A、 B、 C、 D、8. 如图,将矩形绕点顺时针旋转到矩形的位置,旋转角为 . 若 , 则的大小是( ) A、68° B、22° C、28° D、20°9. 如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB , 将线段BM绕点B逆时针旋转60°得到BN , 连结HN . 则在点M运动过程中,线段HN长度的最小值是( )
A、68° B、22° C、28° D、20°9. 如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB , 将线段BM绕点B逆时针旋转60°得到BN , 连结HN . 则在点M运动过程中,线段HN长度的最小值是( ) A、6 B、3 C、2 D、1.510. 如图,矩形ABCD中,AB=2 ,BC=6,P为矩形内一点,连接PA,PB,PC,则PA+PB+PC的最小值是( )
A、6 B、3 C、2 D、1.510. 如图,矩形ABCD中,AB=2 ,BC=6,P为矩形内一点,连接PA,PB,PC,则PA+PB+PC的最小值是( )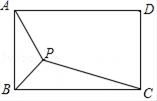 A、4 +3 B、2 C、2 +6 D、411. 如图,已知中, , , 将绕点逆时针旋转得到 , 以下结论:① , ② , ③ , ④ , 正确的有( )
A、4 +3 B、2 C、2 +6 D、411. 如图,已知中, , , 将绕点逆时针旋转得到 , 以下结论:① , ② , ③ , ④ , 正确的有( ) A、①②③ B、①②④ C、①③④ D、②③④12. 如图1,在Rt△ABC中, , , 点D , E分别在边AB , AC上, , 连接DC , 点M、P、N分别为DE、DC、BC的中点.将△ADE绕点A在平面内自由旋转(如图2),若 , , 则△PMN面积的最大值是( )
A、①②③ B、①②④ C、①③④ D、②③④12. 如图1,在Rt△ABC中, , , 点D , E分别在边AB , AC上, , 连接DC , 点M、P、N分别为DE、DC、BC的中点.将△ADE绕点A在平面内自由旋转(如图2),若 , , 则△PMN面积的最大值是( ) A、 B、18 C、 D、13. 如图,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBG.延长AE交CG于点F,连接DE.下列结论:①AF⊥CG,②四边形BEFG是正方形,③若DA=DE,则CF=FG;其中正确的结论是( )
A、 B、18 C、 D、13. 如图,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBG.延长AE交CG于点F,连接DE.下列结论:①AF⊥CG,②四边形BEFG是正方形,③若DA=DE,则CF=FG;其中正确的结论是( ) A、①②③ B、①② C、②③ D、①③14. 如图,O是正内一点, , , , , 将线段BO以点B为旋转中心逆时针旋转60°得到线段 , 下列结论:①点O与的距离为6;②;③;④;⑤点P为内一点,则点P到三个顶点的距离和最小为.其中正确的结论是( )
A、①②③ B、①② C、②③ D、①③14. 如图,O是正内一点, , , , , 将线段BO以点B为旋转中心逆时针旋转60°得到线段 , 下列结论:①点O与的距离为6;②;③;④;⑤点P为内一点,则点P到三个顶点的距离和最小为.其中正确的结论是( ) A、①②③⑤ B、①③④ C、②③④⑤ D、①②⑤15. 在矩形ABCD中,AB=3,AD=5,将矩形ABCD绕点A沿逆时针方向旋转得矩形AEFG,连接BE,当EF刚好经过点D时,线段BE的长是( )
A、①②③⑤ B、①③④ C、②③④⑤ D、①②⑤15. 在矩形ABCD中,AB=3,AD=5,将矩形ABCD绕点A沿逆时针方向旋转得矩形AEFG,连接BE,当EF刚好经过点D时,线段BE的长是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
16. 如图,在Rt△ABC中,∠B=90°,AB=4,BC=6,点D在BC边上,将点A绕点D顺时针旋转90°得到点E,连接DE,CE.当△DCE是等腰三角形时,BD的长为 .
 17. 已知矩形中, , 将绕点顺时针旋转得到 , 与交于点 , 与交于点 , 当点的对应点落在线段上时,线段的长是 .
17. 已知矩形中, , 将绕点顺时针旋转得到 , 与交于点 , 与交于点 , 当点的对应点落在线段上时,线段的长是 . 18. 如图,在△ABC中,∠ACB=90°,AC=8,将△ABC绕点C按逆时针方向旋转得到△A1B1C,满足A1B1∥AC,过点B作BE⊥A1C,垂足为E,连接AE,若S△ABE=3S△ACE , 则AB的长为 .
18. 如图,在△ABC中,∠ACB=90°,AC=8,将△ABC绕点C按逆时针方向旋转得到△A1B1C,满足A1B1∥AC,过点B作BE⊥A1C,垂足为E,连接AE,若S△ABE=3S△ACE , 则AB的长为 . 19. 如图,已知△ABC , ∠ABC<60°,将△ABC绕点A逆时针旋转60°得到△ADE , DE与BC交于点P . 下列结论:
19. 如图,已知△ABC , ∠ABC<60°,将△ABC绕点A逆时针旋转60°得到△ADE , DE与BC交于点P . 下列结论:①∠EPC=60°;
②AC与DE互相平分;
③PA+PC=PE;
④PA平分∠BPE , 其中正确结论的是 .
 20. 如图,点P是在正△ABC内一点.PA=6,PB=8,PC=10,将线段AP绕点A逆时针旋转60°得到线段AP′ , 连结.P′P , P′C , 四边形APCP′的面积为 , S△APB+S△BPC= .
20. 如图,点P是在正△ABC内一点.PA=6,PB=8,PC=10,将线段AP绕点A逆时针旋转60°得到线段AP′ , 连结.P′P , P′C , 四边形APCP′的面积为 , S△APB+S△BPC= . 21. 如图,△ABC是等腰三角形,AB=AC , ∠B=30°,△ADE是直角三角形,∠ADE=90°,∠E=30°,AD=AB . 将△ADE绕点A旋转,AD、AE分别交BC于点F , G , 当∠AGB=75°时, .
21. 如图,△ABC是等腰三角形,AB=AC , ∠B=30°,△ADE是直角三角形,∠ADE=90°,∠E=30°,AD=AB . 将△ADE绕点A旋转,AD、AE分别交BC于点F , G , 当∠AGB=75°时, . 22. 如图,在中, , , , 将绕点B逆时针旋转至 , 连接 , 则线段 .
22. 如图,在中, , , , 将绕点B逆时针旋转至 , 连接 , 则线段 . 23. 如图,在中, , , , 线段绕点旋转到 , 连 , 为的中点,连接 , 则的最大值是 .
23. 如图,在中, , , , 线段绕点旋转到 , 连 , 为的中点,连接 , 则的最大值是 .
三、解答题
-
24. 如图 , 在中, , 为的中点,点在线段上以点为中心,将线段逆时针旋转得到线段 , 连接 , .
 (1)、求证:平分;(2)、如图 , 为的中点,连接试判断与的位置关系,并说明理由;(3)、如图 , 若 , , 连接 , 试说明的面积是一个定值,并求出该定值.25. 已知在中, , , 于 .
(1)、求证:平分;(2)、如图 , 为的中点,连接试判断与的位置关系,并说明理由;(3)、如图 , 若 , , 连接 , 试说明的面积是一个定值,并求出该定值.25. 已知在中, , , 于 .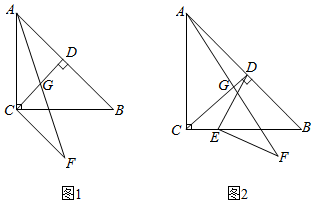 (1)、如图 , 将线段绕点顺时针旋转得到 , 连接交于点求证:;(2)、如图 , 点是线段上一点连接 , 将线段绕点顺时针旋转得到 , 连接交于点 .
(1)、如图 , 将线段绕点顺时针旋转得到 , 连接交于点求证:;(2)、如图 , 点是线段上一点连接 , 将线段绕点顺时针旋转得到 , 连接交于点 .求证:;
若 , , 求的长.
26. 在中, , 将绕点顺时针旋转得到 , 其中点的对应点分别为点 .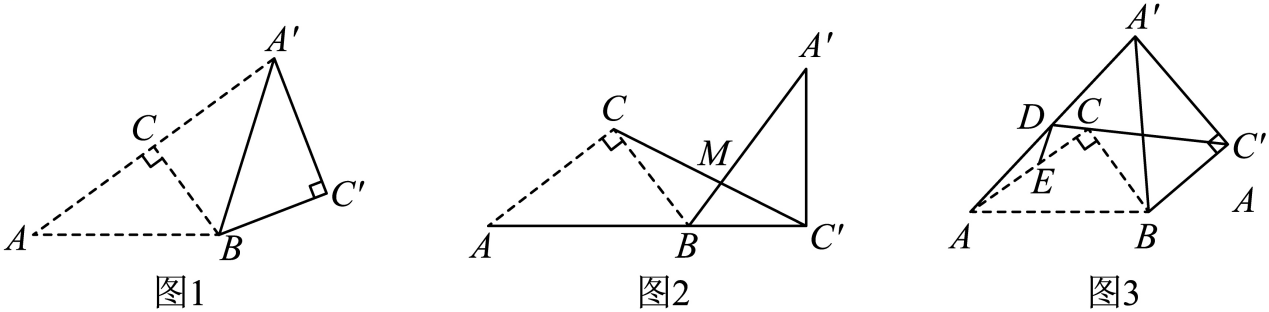 (1)、如图1,当点落在的延长线上时,则的长为;(2)、如图2,当点落在的延长线上时,连接 , 交于点 , 求的长;(3)、如图3,连接 , 直线交于点 , 若E为AC的中点,连接 . 在旋转过程中,是否存在最小值?若存在,请直接写出的最小值;若不存在,请说明理由.27. 在中, , , 为边上一点,连接 .
(1)、如图1,当点落在的延长线上时,则的长为;(2)、如图2,当点落在的延长线上时,连接 , 交于点 , 求的长;(3)、如图3,连接 , 直线交于点 , 若E为AC的中点,连接 . 在旋转过程中,是否存在最小值?若存在,请直接写出的最小值;若不存在,请说明理由.27. 在中, , , 为边上一点,连接 . (1)、如图 , 若 , , 求的长;(2)、如图 , 将的边绕点在同一平面内顺时针旋转得到 , 为延长线上一点,连接若 , , 求证:;(3)、如图 , 在的条件下,为射线上一动点,连接 , , 将沿翻折,得到 , 连接 , 为的中点,连接 , 当的长度最小时,请直接写出的值.
(1)、如图 , 若 , , 求的长;(2)、如图 , 将的边绕点在同一平面内顺时针旋转得到 , 为延长线上一点,连接若 , , 求证:;(3)、如图 , 在的条件下,为射线上一动点,连接 , , 将沿翻折,得到 , 连接 , 为的中点,连接 , 当的长度最小时,请直接写出的值.四、实践探究题
-
28. 如图
 (1)、观察猜想:
(1)、观察猜想:如图1,在直角中, , , 点D为边上一动点(与点B不重合),连接 , 将绕点A逆时针旋转到 , 那么、之间的位置关系为 , 数量关系为;
(2)、数学思考:如图2,在中, , , D、E为上两点,且 , 求证: .
(3)、拓展延伸:如图3,在中, , , , 若以、、为边的三角形是以为斜边的直角三角形,当时,求的长.
29. 在Rt△ABC中,∠ABC=90°,AB=nBC , P为AB上的一点(不与端点重合),过点P作PM⊥AB交AG于点M , 得到△APM . (1)、【问题发现】如图1,当n=1时,P为AB的中点时,CM与BP的数量关系为 ;(2)、【类比探究】如图2,当n=2时,△APM绕点A顺时针旋转,连接CM , BP , 则在旋转过程中CM与BP之间的数量关系是否发生变化?请说明理由;(3)、【拓展延伸】在(2)的条件下,已知AB=4,AP=2,当△APM绕点A顺时针旋转至B , P , M三点共线时,请直接写出线段BM的长.30.(1)、【方法尝试】
(1)、【问题发现】如图1,当n=1时,P为AB的中点时,CM与BP的数量关系为 ;(2)、【类比探究】如图2,当n=2时,△APM绕点A顺时针旋转,连接CM , BP , 则在旋转过程中CM与BP之间的数量关系是否发生变化?请说明理由;(3)、【拓展延伸】在(2)的条件下,已知AB=4,AP=2,当△APM绕点A顺时针旋转至B , P , M三点共线时,请直接写出线段BM的长.30.(1)、【方法尝试】如图1,矩形是矩形以点A为旋转中心,按逆时针方向旋转所得的图形,分别是它们的对角线.则与数量关系 , 位置关系;
 (2)、【类比迁移】
(2)、【类比迁移】如图2,在和中, . 将绕点A在平面内逆时针旋转,设旋转角为α(),连接 . 请判断线段和的数量关系和位置关系,并说明理由;
 (3)、【拓展延伸】
(3)、【拓展延伸】如图3,在中, , 过点A作 , 在射线上取一点D,连接 , 使得 , 请求线段的最大值.
