2024年中考数学考前20天终极冲刺专题之折叠问题
试卷更新日期:2024-05-22 类型:三轮冲刺
一、选择题
-
1. 如图1是长方形纸带,∠DEF=10°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中∠CFE度数是多少( )
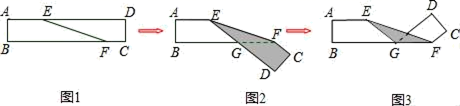 A、160° B、150° C、120° D、110°2. 如图所示,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C'处.若AB=6,BC=9,则BF的长为( )
A、160° B、150° C、120° D、110°2. 如图所示,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C'处.若AB=6,BC=9,则BF的长为( ) A、4 B、3 C、4.5 D、53. 如图,在正方形ABCD中,E为CD边上一点,将△AED沿着AE翻折得到△AEF,点D的对应点F恰好落在对角线AC上,连接BF.若EF=2,则BF2=( )
A、4 B、3 C、4.5 D、53. 如图,在正方形ABCD中,E为CD边上一点,将△AED沿着AE翻折得到△AEF,点D的对应点F恰好落在对角线AC上,连接BF.若EF=2,则BF2=( )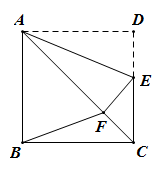 A、4+4 B、6+4 C、12 D、8+44. 如图,将沿直线折叠,使点A落在边上的点F处, , 若 , 则( )
A、4+4 B、6+4 C、12 D、8+44. 如图,将沿直线折叠,使点A落在边上的点F处, , 若 , 则( ) A、 B、 C、 D、5. 如图,正方形ABCD的边长为4,点E在边CD上,且CE=1,连结AE,点F在边AD上,连结BF,把沿BF翻折,点A恰好落在AE上的点G处,下列结论:①AE=BF;②AD=3DF;③;④GE=0.2,其中正确的是( )
A、 B、 C、 D、5. 如图,正方形ABCD的边长为4,点E在边CD上,且CE=1,连结AE,点F在边AD上,连结BF,把沿BF翻折,点A恰好落在AE上的点G处,下列结论:①AE=BF;②AD=3DF;③;④GE=0.2,其中正确的是( )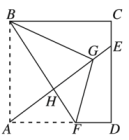 A、①②③④ B、①③④ C、①②③ D、①③6. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( )
A、①②③④ B、①③④ C、①②③ D、①③6. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( ) A、 B、 C、 D、7. 如图,为的直径,将沿翻折,翻折后的弧交于D.若 , , 则图中阴影部分的面积为( )
A、 B、 C、 D、7. 如图,为的直径,将沿翻折,翻折后的弧交于D.若 , , 则图中阴影部分的面积为( ) A、 B、 C、8 D、108. 如图,在中, , , , 点为上一点,点分别是点关于的对称点,则的最小值是( )
A、 B、 C、8 D、108. 如图,在中, , , , 点为上一点,点分别是点关于的对称点,则的最小值是( ) A、 B、 C、4 D、29. 如图,在△ABC中,∠ACB=90°,首先沿着CD折叠,点B落在点E处,然后沿着FG折叠,使得点A与点E重合,则下列说法中( )
A、 B、 C、4 D、29. 如图,在△ABC中,∠ACB=90°,首先沿着CD折叠,点B落在点E处,然后沿着FG折叠,使得点A与点E重合,则下列说法中( )①EF⊥CE;②若BC=3,AC=4,那么 .
 A、①正确,②正确 B、①正确,②错误 C、①错误,②正确 D、①错误,②错误10. 如图,正方形的边长为4,点是边上的一点,将沿着折叠至 , 若、恰好与正方形的中心为圆心的相切,则折痕的长为( )
A、①正确,②正确 B、①正确,②错误 C、①错误,②正确 D、①错误,②错误10. 如图,正方形的边长为4,点是边上的一点,将沿着折叠至 , 若、恰好与正方形的中心为圆心的相切,则折痕的长为( ) A、 B、5 C、 D、以上都不对11. 如图,等边 中,D为AC中点,点P、Q分别为AB、AD上的点, , ,在BD上有一动点E,则 的最小值为( )
A、 B、5 C、 D、以上都不对11. 如图,等边 中,D为AC中点,点P、Q分别为AB、AD上的点, , ,在BD上有一动点E,则 的最小值为( )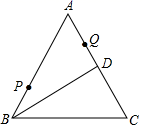 A、7 B、8 C、10 D、1212. 如图,将矩形ABCD沿GE,EC,GF翻折,使得点A,B,D恰好都落在点O处,且点G,O,C在同一条直线上,同时点E,O,F在另一条直线上,小炜同学得出以下结论:①GF∥EC;②AB⑤△COF∽△CEG.其中正确的是( )
A、7 B、8 C、10 D、1212. 如图,将矩形ABCD沿GE,EC,GF翻折,使得点A,B,D恰好都落在点O处,且点G,O,C在同一条直线上,同时点E,O,F在另一条直线上,小炜同学得出以下结论:①GF∥EC;②AB⑤△COF∽△CEG.其中正确的是( ) A、①②③ B、①③④ C、①④⑤ D、②③④13. 如图,在平面直角坐标中,矩形ABCD的边AD=5.OA:OD=1∶4,将矩形ABCD沿直线OE折叠到如图所示的位置,线段OD1恰好经过点B,点C落在y轴的点C1位置,点E的坐标是( )
A、①②③ B、①③④ C、①④⑤ D、②③④13. 如图,在平面直角坐标中,矩形ABCD的边AD=5.OA:OD=1∶4,将矩形ABCD沿直线OE折叠到如图所示的位置,线段OD1恰好经过点B,点C落在y轴的点C1位置,点E的坐标是( ) A、(1,2) B、(-1,2) C、(-1,2) D、(1- , 2)14. 如图,将正方形纸片ABCD沿PQ折叠,使点C的对称点E落在边AB上,点D的对称点为点F,EF为交AD于点G,连接CG交PQ于点H,连接CE.下列四个结论中:①△PBE∽△QFG;②S△CEG=S△CBE+S四边形CDQH;③EC平分∠BEG;④EG2﹣CH2=GQ•GD,正确的是( )
A、(1,2) B、(-1,2) C、(-1,2) D、(1- , 2)14. 如图,将正方形纸片ABCD沿PQ折叠,使点C的对称点E落在边AB上,点D的对称点为点F,EF为交AD于点G,连接CG交PQ于点H,连接CE.下列四个结论中:①△PBE∽△QFG;②S△CEG=S△CBE+S四边形CDQH;③EC平分∠BEG;④EG2﹣CH2=GQ•GD,正确的是( ) A、①③ B、①③④ C、①④ D、①②③④15. 如图,在Rt△ABC中,∠BAC=90°,∠C=30°,将边AB沿着AE翻折,使点B落在BC上的点D处,再将边AC沿着AF翻折,使得C落在AD延长线上的点C′处,两条折痕与斜边BC分别交于E , F . 以下四个结论正确的是( )
A、①③ B、①③④ C、①④ D、①②③④15. 如图,在Rt△ABC中,∠BAC=90°,∠C=30°,将边AB沿着AE翻折,使点B落在BC上的点D处,再将边AC沿着AF翻折,使得C落在AD延长线上的点C′处,两条折痕与斜边BC分别交于E , F . 以下四个结论正确的是( )
①∠EAF=45°;②FC′=BE;③EC=3BE;④FC=(-1)AE .
A、①②③ B、②④ C、①③④ D、①②③④二、填空题
-
16. 如图,在矩形中, , , 点E是边上一点, , 分别在边上取点M , N , 将矩形沿直线翻折,使得点B的对应点恰好落在射线上,点A的对应点是 , 那么折痕的长为;连接 , 线段的最小值为 .
 17. 如图,在平行四边形中, , 点 , 分别为边上异于端点的动点,且 , 连接 , 将四边形沿着折叠得到四边形 . 当点落在平行四边形的边上时,的长为 .
17. 如图,在平行四边形中, , 点 , 分别为边上异于端点的动点,且 , 连接 , 将四边形沿着折叠得到四边形 . 当点落在平行四边形的边上时,的长为 . 18. 如图,平分等边的面积,折叠得到 , 分别与 , 相交于 , 两点.若 , , 则的长是 .
18. 如图,平分等边的面积,折叠得到 , 分别与 , 相交于 , 两点.若 , , 则的长是 . 19. 如图,在正方形的对角线上取一点 , 使得 , 连接 , 将沿翻折得到 , 连接 . 若 , 则的长为 .
19. 如图,在正方形的对角线上取一点 , 使得 , 连接 , 将沿翻折得到 , 连接 . 若 , 则的长为 . 20. 如图,在中,D为斜边的中点,点E在边上,将沿叠至 . 若的延长线经过点D , 平分 , , 则的值为 , 的长为 .
20. 如图,在中,D为斜边的中点,点E在边上,将沿叠至 . 若的延长线经过点D , 平分 , , 则的值为 , 的长为 . 21. 如图,在中, , , 点是边上一点(点不与点 , 重合),将沿翻折,点的对应点为点 , 交于点 , 若 , 则点到线段的距离为 .
21. 如图,在中, , , 点是边上一点(点不与点 , 重合),将沿翻折,点的对应点为点 , 交于点 , 若 , 则点到线段的距离为 . 22. 如图,腰长为22的等腰ABC中,顶角∠A=45°,D为腰AB上的一个动点,将ACD沿CD折叠,点A落在点E处,当CE与ABC的某一条腰垂直时,BD的长为 .
22. 如图,腰长为22的等腰ABC中,顶角∠A=45°,D为腰AB上的一个动点,将ACD沿CD折叠,点A落在点E处,当CE与ABC的某一条腰垂直时,BD的长为 . 23. 如图,将矩形折叠,使得点落在边的三等分点上,且 , 点折叠后的对应点为 , 折痕为 , 连接 , 若 , , 则的长为.
23. 如图,将矩形折叠,使得点落在边的三等分点上,且 , 点折叠后的对应点为 , 折痕为 , 连接 , 若 , , 则的长为.
三、解答题
-
24. 如图,在矩形中, , , 点E是边上一点,连接 , 将沿折叠得到 , 边 , 分别交于点M , N .
 (1)、求证:;(2)、当时.
(1)、求证:;(2)、当时.①求BE的长;
②若点P是边上的动点,连接 , 过点A作的垂线交线段于点Q , 试探究的值是否发生变化,若变化,请说明理由;若不变,请求出的值.
25. 如图,在矩形ABCD中, AB=3,AD=4,E是BC上一动点,将△ABE沿AE折叠后得到△AFE , 点F在矩形ABCD内部,延长AF交CD于点G; (1)、如图1,当∠DAG=30° 时,求BE的长;(2)、如图2,当点E是BC的中点时,求线段GC的长;(3)、如图3,在矩形ABCD中,E , G分别是BC、CD上的一点,AEEG , 将△EGC沿EG翻折得 , 连接 , 若是以AE为腰的等腰三角形,则BE的值为▲ .(直接写出答案)26. 已知,在长方形中, , , , 点E在线段上,点F在线段上,将长方形沿折叠后,点D的对应点是M , 点C的对应点是N .
(1)、如图1,当∠DAG=30° 时,求BE的长;(2)、如图2,当点E是BC的中点时,求线段GC的长;(3)、如图3,在矩形ABCD中,E , G分别是BC、CD上的一点,AEEG , 将△EGC沿EG翻折得 , 连接 , 若是以AE为腰的等腰三角形,则BE的值为▲ .(直接写出答案)26. 已知,在长方形中, , , , 点E在线段上,点F在线段上,将长方形沿折叠后,点D的对应点是M , 点C的对应点是N . (1)、如图1,若 , 求的度数;(2)、如图2,将四边形沿继续折叠,点N的对应点为G , 探索与的数量关系,并证明你的结论;(3)、如图3,P是直线和线段的交点,将四边形沿折叠,点A的对应点是O , 点B的对应点是Q . 请直接写出和的数量关系.27. 等边中,于点 , 点为边上一动点,连接 , 点关于直线的对称点为点 , 连接 .
(1)、如图1,若 , 求的度数;(2)、如图2,将四边形沿继续折叠,点N的对应点为G , 探索与的数量关系,并证明你的结论;(3)、如图3,P是直线和线段的交点,将四边形沿折叠,点A的对应点是O , 点B的对应点是Q . 请直接写出和的数量关系.27. 等边中,于点 , 点为边上一动点,连接 , 点关于直线的对称点为点 , 连接 . (1)、如图1,点恰好落在的延长线上,则求;(2)、过点作交于点 , 连接交于点 .
(1)、如图1,点恰好落在的延长线上,则求;(2)、过点作交于点 , 连接交于点 .①如图2,试判断线段、和之间的数量关系,并说明理由:
②如图3,直线交于点 , 连接点运动的过程中.当取最小值时,请直接写出线段的长度.