广东省潮州市2023-2024学年七年级下学期数学期中试题

试卷更新日期：2024-05-22 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分）

1. 如图所示的图案分别是三菱、大众、奥迪、奔驰汽车的车标，其中可以看成是由“基本图案”经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 在实数 $\sqrt[3]{27}$ ， $- π$ ， $\sqrt{16}$ ， $\frac{22}{7}$ ， 0.1010010001…（相邻两个1之间多一个0）中，有（）个无理数．

A、1 B、2 C、3 D、4

查看试题解析
3. 下列各式表示正确的是（）

A、 $\pm \sqrt{25} = \pm 5$ B、 $\pm \sqrt{25} = 5$ C、 $\sqrt{25} = \pm 5$ D、 $\pm \sqrt{(- 5)^{2}} = - 5$

查看试题解析
4. 已知 $| a + 2 | + | b - 3 | = 0$ ，那么点（a ， b）位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 下面命题：
①负数没有立方根；
②一个实数的立方根不是正数就是负数；
③一个正数或负数的立方根与这个数同号；
④如果一个数的立方根是这个数本身，那么这个数是1或0.
其中真命题的是（）

A、①② B、③④ C、③ D、④

查看试题解析
6. 如图，是我们学过的用直尺和三角尺画平行线的方法示意图，画图的原理是（）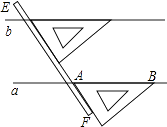

A、同位角相等，两直线平行 B、内错角相等，两直线平行 C、两直线平行，同位角相等 D、两直线平行，内错角相等

查看试题解析
7. 把一块直尺与一块三角板如下图放置，若∠1＝40°，则∠2的度数为（）

A、115° B、120° C、125° D、130°

查看试题解析
8. 如图在一块长14m、宽6m的长方形场地上，有一条弯曲的道路，其余的部分为绿化区，道路的左边线向右平移3m就是它的右边线，则绿化区的面积是（）

A、96m² B、72m² C、66m² D、56m²

查看试题解析
9. 在平面直角坐标系中，点A（a＋1，a－1）是x轴上一点，线段AB＝2，若AB//y轴，则点B的坐标是（）

A、（2，2） B、（－2，2） C、（－2，2）或（－2，2） D、（2，2）或（2，－2）

查看试题解析
10. 已知点A（1，0），B（0，2），点P在x轴上，且三角形PAB的面积为5，则点P的坐标是（）

A、（－4，0） B、（10，0） C、（10，0）或（6，0） D、（－4，0）或（6，0）

查看试题解析

二、填空题（本大题共5小题，每小题3分，共15分）

11. $\sqrt{81}$ 的算术平方根是

查看试题解析
12. 将一副透明的直角三角尺按如图所示方式放置，若AE//BC ，则∠CAD＝．

查看试题解析
13. 已知： $\sqrt[3]{1.12} \approx 1.038, \sqrt[3]{11.2} \approx 2.237, \sqrt[3]{112} \approx 4.820$ ，则 $\sqrt[3]{1120} \approx$ ．

查看试题解析
14. 如图，将三角形ABC沿BC方向平移得到三角形DEF ， AB＝10，DH＝4，平移距离为6，则阴影部分的面积为．

查看试题解析
15. 如图，在平面直角坐标系中，A（1，1），B（－1，1），C（－1，－2），D（1，－2）．点P从点A出发，并按A→B→C→D→A……的规律在四边形ABCD的边上运动，当点P运动的路程为2024个单位长度时，则点P所在位置的点的坐标是．

查看试题解析

三、解答题（一）（本大题共3小题，每小题5分，共15分）

16. 计算： $(- 1)^{2024} - \sqrt{4} + \sqrt{(- 3)^{2}} + \sqrt[3]{- 8}$

查看试题解析
17. 如图，BD平分∠ABC ， F在AB上，G在AC上，FC与BD相交于点H ， ∠3＋∠4＝180°，试说明∠1＝∠2.（请通过填空完善下列推理过程）
解：∵∠3＋∠4＝180°（已知），
∠FHD＝∠4（对顶角相等）
∴∠3＋        ▲        ＝180°．
∴FG∥BD（        ▲        ）
∴∠1＝（        ▲        ）
∵BD平分∠ABC ，
∴∠ABD＝        ▲         ．
∴∠1＝∠2

查看试题解析
18. 如图，在平面直角坐标系中，三角形ABC三个顶点的坐标分别为A（－4，－1），B（－5，－4），C（－1，－3），已知三角形ABC经过平移得到三角形 $A^{'} B^{'} C^{'}$ ，且三角形ABC中任意一点P（x ， y）经过平移后的对应点为 $P^{'}$ （x＋6，y＋4），请写出点 $A^{'}, C^{'}$ 的坐标，并画出三角形 $A^{'} B^{'} C^{'}$ ．

查看试题解析

四、解答题（二）（本大题共3小题，6＋6＋8＝20分）

19. 实数a ， b ， c在数轴上的对应点如图所示，化简 $| b - c | - \sqrt{(a - c)^{2}} + \sqrt[3]{a^{3}}$ ．

查看试题解析
20. 如图，已知点P在CD上，∠BAP＋∠APD＝180°，∠1＝∠2，求证：∠E＝∠F ．

查看试题解析
21. 已知：正数x的平方根是a＋3与2a－15，且 $\sqrt{2 b - 1} = 3$ ．

(1)、求x的值；

(2)、求a＋b－1的立方根．

查看试题解析

五、解答题（三）（本大题共2小题，10＋10＝20分）

22. 【阅读理解】先阅读下列一段文字，再解答问题．
已知在平面内有两点 $P_{1} (x_{1}, y_{1}), P_{2} (x_{2}, y_{2})$ ，其两点间的距离公式为 $p_{1} p_{2} = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}}$ ，同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为 $| x_{2} - x_{1} |$ 或 $| y_{2} - y_{1} |$ ．

(1)、已知点A（4，4），B（1，0），试求A ， B两点间的距离；

(2)、已知点A ， B在平行于x轴的直线上，点A横坐标为6，点B横坐标为2，试求A ， B两点间的
距离；

(3)、应用平面内两点间的距离公式，求式子 $\sqrt{x^{2} + (y + 1)^{2}} + \sqrt{(x + 6)^{2} + (y - 7)^{2}}$ 的最小值．

查看试题解析
23. 【综合与探究】如图1，在平面直角坐标系中，已知点A（－1，0）、点B（3，0）、点C（0，2），点D在第一象限，CD//AB且CD＝AB ，连接AC ， BD ．

(1)、直接写出点D的坐标；

(2)、若点M在y轴的正半轴上，且S_△_ODM＝2S_△_AOC ，求点M的坐标；

(3)、若点P是线段BD延长线上的一点（如图2）．连接PC、PO ，请判断∠CPO ， ∠DCP与∠BOP之间的数量关系，并证明你的结论．

查看试题解析