2024年中考数学考前20天终极冲刺专题之线段最值(二)
试卷更新日期:2024-05-21 类型:三轮冲刺
一、选择题
-
1. 如图,▱ABCD中,AB=3,AD=5,AC⊥AB , E、F为线段BD上两动点(不与端点重合)且EF=BD , 连接AE , CF , 当点EF运动时,对AE+CF的描述正确的是( )
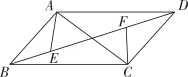 A、等于定值5- B、有最大值 C、有最小值 D、有最小值2. 如图,在边长为a的正方形中,E是对角线上一点,且 , 点P是上一动点,则点P到边 , 的距离之和的值( )
A、等于定值5- B、有最大值 C、有最小值 D、有最小值2. 如图,在边长为a的正方形中,E是对角线上一点,且 , 点P是上一动点,则点P到边 , 的距离之和的值( ) A、有最大值a B、有最小值 C、是定值a D、是定值3. 如图,AB为⊙O的直径,AB=8,点C为半圆AB上一动点,以BC为边向⊙O外作正ΔBCD(点D在直线AB的上方),连接OD,则线段OD的( )
A、有最大值a B、有最小值 C、是定值a D、是定值3. 如图,AB为⊙O的直径,AB=8,点C为半圆AB上一动点,以BC为边向⊙O外作正ΔBCD(点D在直线AB的上方),连接OD,则线段OD的( )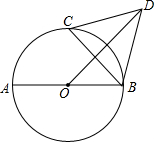 A、随点C的运动而变化,最小值为
A、随点C的运动而变化,最小值为 B、随点C的运动而变化,最大值为8
C、随点C的运动而变化,最大值为
B、随点C的运动而变化,最大值为8
C、随点C的运动而变化,最大值为 D、随点C的运动而变化,但无最值
4. 如图,的半径是 , 点是直线上一动点,过点作的切线,切点为 , 连接 , , 则的最小值为( )
D、随点C的运动而变化,但无最值
4. 如图,的半径是 , 点是直线上一动点,过点作的切线,切点为 , 连接 , , 则的最小值为( )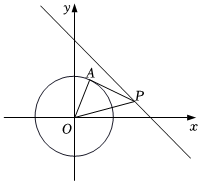 A、 B、 C、 D、5. 如图,在矩形ABCD中,AB=4,AD=6,点P在AD上,点Q在BC上,且AP = CQ,连接CP,QD,则PC + QD的最小值为( )
A、 B、 C、 D、5. 如图,在矩形ABCD中,AB=4,AD=6,点P在AD上,点Q在BC上,且AP = CQ,连接CP,QD,则PC + QD的最小值为( ) A、8 B、10 C、12 D、206. 如图,在中, , 于点D , P是上的一个动点,以点P为直角顶点向右作等腰 , 连接 , 则的最小值为( )
A、8 B、10 C、12 D、206. 如图,在中, , 于点D , P是上的一个动点,以点P为直角顶点向右作等腰 , 连接 , 则的最小值为( ) A、1 B、 C、2 D、7. 在周长为 的正方形 中,点 是 边的中点,点 为对角线 上的一个动点,则 的最小值为( )
A、1 B、 C、2 D、7. 在周长为 的正方形 中,点 是 边的中点,点 为对角线 上的一个动点,则 的最小值为( )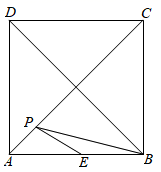 A、2 B、 C、 D、8. 如图,在平行四边形ABCD中,AD=4,∠A=60°,E是边DC延长线上一点,连接BE , 以BE为边作等边三角形BEF , 连接FC , 则FC的最小值是( )
A、2 B、 C、 D、8. 如图,在平行四边形ABCD中,AD=4,∠A=60°,E是边DC延长线上一点,连接BE , 以BE为边作等边三角形BEF , 连接FC , 则FC的最小值是( )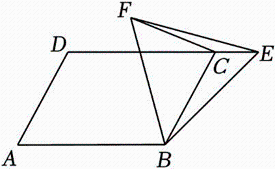 A、 B、2 C、 D、9. 如图,矩形中, , , G是的中点,线段在边上左右滑动,若 , 则的最小值为( )
A、 B、2 C、 D、9. 如图,矩形中, , , G是的中点,线段在边上左右滑动,若 , 则的最小值为( ) A、4 B、5 C、 D、10. 如图,AB是⊙O的直径,AB=10,点C是圆上不与A , B重合的点,CD平分∠ACB , 交⊙O于D , AE平分∠CAB , 交CD于E . 有以下说法:
A、4 B、5 C、 D、10. 如图,AB是⊙O的直径,AB=10,点C是圆上不与A , B重合的点,CD平分∠ACB , 交⊙O于D , AE平分∠CAB , 交CD于E . 有以下说法:①点D是定点;
②AC•BC的最大值为50;
③D为△ABE的外心;
④CA+CB的最大值为 .
其中正确的有( )
 A、1个 B、2个 C、3个 D、4个11. 如图,的半径弦于点E , C是上一点, , 的最大值为18,则的长为( )
A、1个 B、2个 C、3个 D、4个11. 如图,的半径弦于点E , C是上一点, , 的最大值为18,则的长为( ) A、8 B、6 C、4 D、212. 如图,在平面直角坐标系中,正方形的两个顶点A、B是坐标轴上的动点,若正方形的边长为4,则线段长的最大值是( )
A、8 B、6 C、4 D、212. 如图,在平面直角坐标系中,正方形的两个顶点A、B是坐标轴上的动点,若正方形的边长为4,则线段长的最大值是( )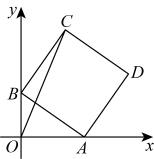 A、 B、 C、 D、813. 如图,△ABC中,∠ABC=90°, , D是AB中点,P是以A为圆心,以AD为半径的圆上的动点,连接PB、PC,则 的最大值为( )
A、 B、 C、 D、813. 如图,△ABC中,∠ABC=90°, , D是AB中点,P是以A为圆心,以AD为半径的圆上的动点,连接PB、PC,则 的最大值为( )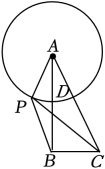 A、 B、 C、 D、14. 如图,中, , , 则边的最大值为( )
A、 B、 C、 D、14. 如图,中, , , 则边的最大值为( ) A、 B、 C、8 D、15. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4直线l经过点B,AE⊥l于点E,CF⊥l于点F,则AE+CF的最大值为( )
A、 B、 C、8 D、15. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4直线l经过点B,AE⊥l于点E,CF⊥l于点F,则AE+CF的最大值为( ) A、 B、5 C、 D、16. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD中,M,N分别是AB,BC上的格点,BM=4,BN=2.若点Р是这个网格图形中的格点,连结PM,PN,则所有满足∠MPN=45°的△PMN中,边PM的长的最大值为( )
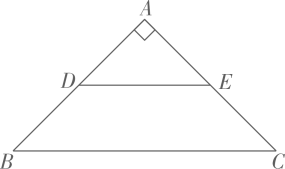
A、 B、5 C、 D、16. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD中,M,N分别是AB,BC上的格点,BM=4,BN=2.若点Р是这个网格图形中的格点,连结PM,PN,则所有满足∠MPN=45°的△PMN中,边PM的长的最大值为( )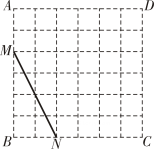 A、 B、6 C、 D、17. 如图,在中, , 点D、E分别是的中点.将绕点A顺时针旋转 , 射线与射线交于点P,在这个旋转过程中有下列结论:
A、 B、6 C、 D、17. 如图,在中, , 点D、E分别是的中点.将绕点A顺时针旋转 , 射线与射线交于点P,在这个旋转过程中有下列结论:①;②存在最大值为;③存在最小值为;④点P运动的路径长为 . 其中,正确的是( )
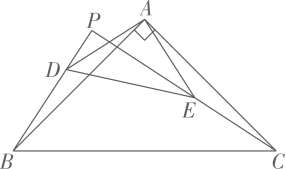 A、①③④ B、①②④ C、①②③ D、②③④18. 如图,函数与函数的图象交于A,B两点,点P在以C(-2,0)为圆心,1为半径的圆C上,Q是AP的中点,则OQ长的最大值为( )
A、①③④ B、①②④ C、①②③ D、②③④18. 如图,函数与函数的图象交于A,B两点,点P在以C(-2,0)为圆心,1为半径的圆C上,Q是AP的中点,则OQ长的最大值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
19. 如图,四边形是正方形,边长为2,点E , F分别是 , 上的动点,且 , 则的最小值为 .
 20. 如图,矩形ABCD中,AB=4,AD=2,E为AB的中点,F为EC上一动点,P为DF中点,连接PB , 则PB的最小值 .
20. 如图,矩形ABCD中,AB=4,AD=2,E为AB的中点,F为EC上一动点,P为DF中点,连接PB , 则PB的最小值 . 21. 如图,AB是半圆O的直径,点C在半圆上,AB=5,AC=4,D是 上的一个动点,连接AD.过点C作CE⊥AD于E,连接BE,则BE的最小值是。
21. 如图,AB是半圆O的直径,点C在半圆上,AB=5,AC=4,D是 上的一个动点,连接AD.过点C作CE⊥AD于E,连接BE,则BE的最小值是。 22. 如图,矩形ABCD中,AB=6,BC=8,点E、F分别是边AB、BC上的动点,在运动过程中始终保持AE=CF , 连接EF , 取EF中点G , 连接AG , 则AG的最小值是 .
22. 如图,矩形ABCD中,AB=6,BC=8,点E、F分别是边AB、BC上的动点,在运动过程中始终保持AE=CF , 连接EF , 取EF中点G , 连接AG , 则AG的最小值是 . 23. 如图,内接于 , 已知是直径, , , 点在直径上方的半圆上运动,连结交于点 , 则的最大值为 .
23. 如图,内接于 , 已知是直径, , , 点在直径上方的半圆上运动,连结交于点 , 则的最大值为 . 24. 如图,⊙M的半径为4,圆心M的坐标为(6,8),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点.若点A、点B关于原点O对称,则当AB取最大值时,点A的坐标为 .
24. 如图,⊙M的半径为4,圆心M的坐标为(6,8),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点.若点A、点B关于原点O对称,则当AB取最大值时,点A的坐标为 .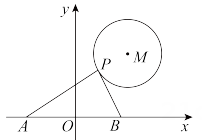 25. 如图,在菱形ABCD中,AB=6,菱形的面积为30;折叠该菱形,使点A落在边BC上的点M处,折痕分别与边AB,AD相交于点E,F,当点M的位置变化时,DF的长的最大值为.
25. 如图,在菱形ABCD中,AB=6,菱形的面积为30;折叠该菱形,使点A落在边BC上的点M处,折痕分别与边AB,AD相交于点E,F,当点M的位置变化时,DF的长的最大值为. 26. 如图,在中,为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则的面积是 , 面积的最大值为.
26. 如图,在中,为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则的面积是 , 面积的最大值为. 27. 如图,线段为的直径,点C在的延长线上, , , 点P是上一动点,连接 , 以为斜边在的上方作Rt , 且使 , 连接 , 则长的最大值为 .
27. 如图,线段为的直径,点C在的延长线上, , , 点P是上一动点,连接 , 以为斜边在的上方作Rt , 且使 , 连接 , 则长的最大值为 .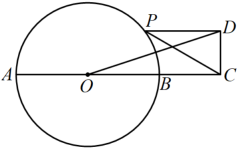 28. 如图,P为Rt△ABC内一点,其中∠BAC=90°,并且PA=3,PB=7,PC=9,则BC的最大值为.
28. 如图,P为Rt△ABC内一点,其中∠BAC=90°,并且PA=3,PB=7,PC=9,则BC的最大值为. 29. 如图,在菱形中, , 对角线、交于点 , , 点为的中点,点为上一点,且 , 点为上一动点,连接、 , 则的最大值为 .
29. 如图,在菱形中, , 对角线、交于点 , , 点为的中点,点为上一点,且 , 点为上一动点,连接、 , 则的最大值为 . 30. 如图所示, , 半径为2的圆O内切于.P为圆O上一动点,过点P作、分别垂直于的两边,垂足为M、N,则的取值范围为 .
30. 如图所示, , 半径为2的圆O内切于.P为圆O上一动点,过点P作、分别垂直于的两边,垂足为M、N,则的取值范围为 . 31. 在矩形中, , , 点是平面内一动点,且满足 , 为的中点,点运动过程中线段长度的取值范围是 .
31. 在矩形中, , , 点是平面内一动点,且满足 , 为的中点,点运动过程中线段长度的取值范围是 . 32. 如图,AB是半径为4的⊙O的弦,且AB=6,将沿着弦AB折叠,点C是折叠后的上一动点,连接并延长BC交⊙O于点D , 点E是CD的中点,连接EO , 则EO的最小值为 .
32. 如图,AB是半径为4的⊙O的弦,且AB=6,将沿着弦AB折叠,点C是折叠后的上一动点,连接并延长BC交⊙O于点D , 点E是CD的中点,连接EO , 则EO的最小值为 . 33. 如图,在Rt△ABC中,AB⊥BC,AB=6,BC=4.P是△ABC内部的一个动点,且满足∠PAB=∠PBC ,则线段CP长的最小值为
33. 如图,在Rt△ABC中,AB⊥BC,AB=6,BC=4.P是△ABC内部的一个动点,且满足∠PAB=∠PBC ,则线段CP长的最小值为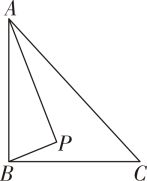 34. 在Rt△ABC中,∠BAC=30°,斜边AB=2 ,动点P在AB边上,动点Q在AC边上,且∠CPQ=90°,则线段CQ长的最小值= .
34. 在Rt△ABC中,∠BAC=30°,斜边AB=2 ,动点P在AB边上,动点Q在AC边上,且∠CPQ=90°,则线段CQ长的最小值= .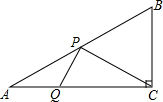 35. 如图, , 分别是边长为的等边三角形的两边 , 上的动点,且 , 与交于点 , 则点到点的最小值为 .
35. 如图, , 分别是边长为的等边三角形的两边 , 上的动点,且 , 与交于点 , 则点到点的最小值为 . 36. 中, , , , E是AC的中点,MN分别是边AB、BC上的动点,D也是BC边上的一个动点,以CD为直径作 , 连接ED交于F,连接FM,MN,则的最小值为.
36. 中, , , , E是AC的中点,MN分别是边AB、BC上的动点,D也是BC边上的一个动点,以CD为直径作 , 连接ED交于F,连接FM,MN,则的最小值为.
三、综合题
-
37. 对于任意正实数, , , ,只有 时,等号成立.结论:在 (,均为正实数)中,若为定值,则 ,只有当 时,a+b有最小值 .根据上述内容,回答下列问题:(1)、初步探究:若 ,只有当 时,有 最小值;(2)、深入思考:下面一组图是由4个全等的矩形围成的大正方形,中空部分是小正方形,矩形的长和宽分别为,试利用大正方形与四个矩形的面积的大小关系,验证 ,并指出等号成立时的条件;
 (3)、拓展延伸:如图,已知 , ,点是第一象限内的一个动点,过点向坐标轴作垂线,分别交轴和轴于,两点,矩形的面积始终为48,求四边形面积的最小值以及此时点的坐标.
(3)、拓展延伸:如图,已知 , ,点是第一象限内的一个动点,过点向坐标轴作垂线,分别交轴和轴于,两点,矩形的面积始终为48,求四边形面积的最小值以及此时点的坐标. 38. 对于平面直角坐标系xOy中的图形P,Q,给出如下定义:M为图形P上任意一点,N为图形Q上任意一点,如果M,N两点间的距离有最小值,那么称这个最小值为图形P,Q间的“非常距离”,记作 . 已知点 , , 连接AB.
38. 对于平面直角坐标系xOy中的图形P,Q,给出如下定义:M为图形P上任意一点,N为图形Q上任意一点,如果M,N两点间的距离有最小值,那么称这个最小值为图形P,Q间的“非常距离”,记作 . 已知点 , , 连接AB. (1)、d(点O,AB)=;(2)、⊙O半径为r,若 , 直接写出r的取值范围;(3)、⊙O半径为r,若将点A绕点B逆时针旋转 , 得到点 .
(1)、d(点O,AB)=;(2)、⊙O半径为r,若 , 直接写出r的取值范围;(3)、⊙O半径为r,若将点A绕点B逆时针旋转 , 得到点 .①当时 , 求出此时r的值;
②对于取定的r值,若存在两个α使 , 直接写出r的范围.
39. 对于平面内的点P和图形M , 给出如下定义:以点P为圆心,r为半径作圆,若 与图形M有交点,且半径r存在最大值与最小值,则将半径r的最大值与最小值的差称为点P视角下图形M的“宽度 ”.(1)、如图1.点 , . ①在点O视角下,则线段 的“宽度 ”为;
①在点O视角下,则线段 的“宽度 ”为;②若 半径为1.5,在点A视角下, 的“宽度 ”为;
(2)、如图2, 半径为2,点P为直线 上一点.求点P视角下 “宽度 ”的取值范围;(3)、已知点 ,直线 与x轴,y轴分别交于点D , E .若随着点C位置的变化,使得在所有点K的视角下,线段 的“宽度”均满足 ,直接写出m的取值范围.
40. 在平面直角坐标系 中, 的半径为 , , 为 外两点, .给出如下定义:平移线段 ,使平移后的线段 成为 的弦(点 , 分别为点 , 的对应点),线段 长度的最小值称为线段 到 的“优距离”.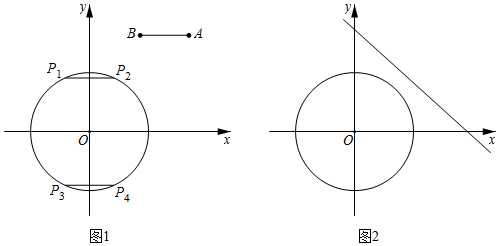 (1)、如图1, 中的弦 、 是由线段 平移而得,这两条弦的位置关系是;在点 , , , 中,连接点 与点的线段的长度等于线段 到 的“优距离”;(2)、若点 , ,线段 的长度是线段 到 的“优距离”,则点 的坐标为;(3)、如图2,若 , 是直线 上两个动点,记线段 到 的“优距离”为 ,则 的最小值是;请你在图2中画出 取得最小值时的示意图,并标记相应的字母.
(1)、如图1, 中的弦 、 是由线段 平移而得,这两条弦的位置关系是;在点 , , , 中,连接点 与点的线段的长度等于线段 到 的“优距离”;(2)、若点 , ,线段 的长度是线段 到 的“优距离”,则点 的坐标为;(3)、如图2,若 , 是直线 上两个动点,记线段 到 的“优距离”为 ,则 的最小值是;请你在图2中画出 取得最小值时的示意图,并标记相应的字母.