备考2024年中考数学重难创新题6 与四边形有关的证明与计算
试卷更新日期:2024-05-21 类型:二轮复习
一、新考法-探索图形中的数量关系
-
1. 如图,正方形 , 点在边上,且 , , 垂足为 , 且交于点 , 与交于点 , 延长至 , 使 , 连接 , 有如下结论:;;; . 上述结论中,正确的个数是( )
 A、个 B、个 C、个 D、个2. 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE= ;④AF=2 ,其中正确结论的个数有( )
A、个 B、个 C、个 D、个2. 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE= ;④AF=2 ,其中正确结论的个数有( )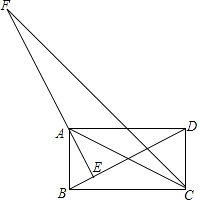 A、1个 B、2个 C、3个 D、4个3. 如图,正方形ABCD的对角线相交于O点,BE平分∠ABO交AO于E点,CF⊥BE于F点,交BO于G点,连接EG、OF,下列四个结论:①CE=CB;②AE=OE;③OF=CG,其中正确的结论只有( )
A、1个 B、2个 C、3个 D、4个3. 如图,正方形ABCD的对角线相交于O点,BE平分∠ABO交AO于E点,CF⊥BE于F点,交BO于G点,连接EG、OF,下列四个结论:①CE=CB;②AE=OE;③OF=CG,其中正确的结论只有( )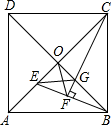 A、①②③ B、②③ C、①③ D、①②
A、①②③ B、②③ C、①③ D、①②二、新考法-结合数学文化
-
4. 文艺复兴时期,意大利艺术大师达·芬奇曾研究过圆弧所围成的许多图形的面积问题.如图称为达·芬奇的“猫眼”,可看成圆与正方形的各边均相切,切点分别为A,B,C,D,劣弧BD所在圆的圆心为点A或点C.若正方形的边长为2,则图中阴影部分的面积为( )
 A、 B、2 C、π-1 D、5. 图1是第七届国际数学教育大会(ICME)的会徽,图2由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF,使点D,E,F分别在边OC,OB,BC上,过点作于点.当时,EH的长为( )
A、 B、2 C、π-1 D、5. 图1是第七届国际数学教育大会(ICME)的会徽,图2由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF,使点D,E,F分别在边OC,OB,BC上,过点作于点.当时,EH的长为( )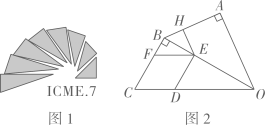 A、 B、 C、 D、6. 第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形()和中间一个小正方形拼成的大正方形中, , 连接 . 设 , 若正方形与正方形的面积之比为 , 则( )
A、 B、 C、 D、6. 第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形()和中间一个小正方形拼成的大正方形中, , 连接 . 设 , 若正方形与正方形的面积之比为 , 则( ) A、5 B、4 C、3 D、27. 公元3世纪初,我国学家赵爽证明勾定理的图形称为“弦图”.1876年类国总统Garfeild用图1(点C、点B、点C'三点共线)进行了勾股定理的证明.△ACB与△BC'B'是一样的直角三角板,两直角边长为a,b,斜边是c.
A、5 B、4 C、3 D、27. 公元3世纪初,我国学家赵爽证明勾定理的图形称为“弦图”.1876年类国总统Garfeild用图1(点C、点B、点C'三点共线)进行了勾股定理的证明.△ACB与△BC'B'是一样的直角三角板,两直角边长为a,b,斜边是c. (1)、请用此图1证明勾股定理.(2)、扩展应用1:
(1)、请用此图1证明勾股定理.(2)、扩展应用1:如图2,以△ABC的边AB和边AC为边长分别向外作正方形ABFH和正方形CED,过点F、E分别作BC的垂线段FM、EN,那么FM、EN、BC的数量关系是怎样?:说明理由.
(3)、扩展应用2:如图3,在两平行线m、n之间有一正方形ABCD,已知点A和点C分别在直m、n上,过点D作直线l∥n∥m,已知l、n之间距离为l,l、m之间距离为2.直接出正方形的面积是.
三、新考法-补全图形,注重过程性学习
-
8.
如图,在梯形ABCD中,AD∥BC,AD=CD,过点A作AE∥DC交BC于点E.
(1)求证:四边形AECD是菱形.
(2)在(1)的条件下,若∠B=30°,AE⊥AB,以点A为圆心,AE的长为半径画弧交BE于点F,连接AF,在图中,用尺规补齐图形(仅保留作图痕迹),并证明点F是BE的中点.
 9.
9.四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.
(1)如图1,当点E、F在线段AD上时,①求证:∠DAG=∠DCG;②猜想AG与BE的位置关系,并加以证明;
(2)如图2,在(1)条件下,连接HO,试说明HO平分∠BHG;
(3)当点E、F运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出∠BHO的度数.
 10. 如图,在中,于点 , 求AD的长.小明同学利用翻折,巧妙地解答了此题,
10. 如图,在中,于点 , 求AD的长.小明同学利用翻折,巧妙地解答了此题,小明的思路:①以AB为对称轴,画出的对称图形,点的对称点为点;
②以AC为对称轴,画出的对称图形,点的对称点为点;
③延长EB和FC相交于点;
④设 , 建立关于的方程模型,从而求出AD的长.
按小明的思路探究并解答下列问题:
 (1)、补全图形,判断四边形AEGF的形状,并证明;(2)、求AD的长.11. 如图,已知,点E在正方形ABCD的BC边上(不与点B,C重合),AC是对角线,过点E作AC的垂线,垂足为G , 连接BG , DG . 把线段DG绕着G点顺时针旋转,使D点的对应点F点刚好落在BC延长线上,根据题意补全图形.
(1)、补全图形,判断四边形AEGF的形状,并证明;(2)、求AD的长.11. 如图,已知,点E在正方形ABCD的BC边上(不与点B,C重合),AC是对角线,过点E作AC的垂线,垂足为G , 连接BG , DG . 把线段DG绕着G点顺时针旋转,使D点的对应点F点刚好落在BC延长线上,根据题意补全图形. (1)、证明: ;(2)、连接DF , 用等式表示线段BG与DF的数量关系,并证明.
(1)、证明: ;(2)、连接DF , 用等式表示线段BG与DF的数量关系,并证明.四、新考法-结合无刻度直尺作图
-
12. 图 , 图都是由边长为的小等边三角形构成的网格,每个小等边三角形的顶点称为格点,线段的端点在格点上,分别按要求画出图形:
 (1)、在图中画出两个以为斜边的直角三角形 , 且点在格点上;(2)、在图中画出一个以为对角线的菱形 , 且 , 在格点上.13. 图、图均是的正方形网格,每个小正方形的边长均为 , 小正方形的顶点称为格点用直尺在给定的网格中按要求画图,所画图形的顶点均在格点上.
(1)、在图中画出两个以为斜边的直角三角形 , 且点在格点上;(2)、在图中画出一个以为对角线的菱形 , 且 , 在格点上.13. 图、图均是的正方形网格,每个小正方形的边长均为 , 小正方形的顶点称为格点用直尺在给定的网格中按要求画图,所画图形的顶点均在格点上.
 (1)、在图中,以线段为一边画一个菱形;
(1)、在图中,以线段为一边画一个菱形;
(2)、在图中,以点为顶点,另外三个顶点也在格点上,画一个面积最大的正方形.14. 如图,在方格纸中,点A,B,P都在格点上.请按要求画出以AB为边的格点图形(图形的每个端点都在格点上).
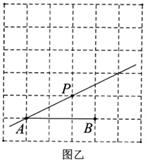 (1)、在图甲中画出一个三角形ABC,使直线BP平分该三角形的面积.(2)、在图乙中画出一个至少有一组对边平行的四边形ABMN,使直线AP平分该四边形的面积.
(1)、在图甲中画出一个三角形ABC,使直线BP平分该三角形的面积.(2)、在图乙中画出一个至少有一组对边平行的四边形ABMN,使直线AP平分该四边形的面积.五、新考法-结合尺规作图
-
15. 如图,在▱ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于 BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(Ⅰ)根据以上尺规作图的过程,求证:四边形ABEF是菱形;
(Ⅱ)若菱形ABEF的周长为16,AE=4 ,求∠C的大小.
 16. 综合与实践
16. 综合与实践数学活动课上,同学们用尺规作图法探究在菱形内部作一点到该菱形三个顶点的距离相等.
【动手操作]如图,已知菱形 , 求作点E , 使得点E到三个顶点A , D , C的距离相等.小红同学设计如下作图步骤∶

①连接;
②分别以点A , D为圆心,大于的长为半径分别在的上方与下方作弧:上方两弧交于点M , 下方两弧交于点N , 作直线交于点E .
③连接 , , 则 .
(1)、根据小红同学设计的尺规作图步骤,在题图中完成作图过程(要求∶用尺规作图并保留作图痕迹)(2)、证明: .(3)、当时,求与的面积比.17. 如图,已知 .
⑴请用尺规作图作出的平分线交于点;
⑵请用尺规作图作出线段的垂直平分线交于点 , 交于点;
⑶连接和 , 直接写出四边形的形状.
六、新考法-方案选取
-
18. 一块直角三角形木板的条直角边AB长为1.5m,面积为1.5m2 . 工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两名同学设计加工方案.甲设计方案如图①,乙设计方案如图②.你认为哪名同学设计的方案较好?试说明理由(加工损耗忽略不计,计算结果可保留分数).
 19. 如图所示,在半径为5、圆心角为的扇形AOB内部作一个正方形CDEF.有以下两种方案:方案一为点D,E在OB上,点在OA上,点在扇形的弧上;方案二为点在OB上,点在OA上,点E,F在扇形的弧上.问:哪种方案的正方形CDEF的面积更大?请说明理由.
19. 如图所示,在半径为5、圆心角为的扇形AOB内部作一个正方形CDEF.有以下两种方案:方案一为点D,E在OB上,点在OA上,点在扇形的弧上;方案二为点在OB上,点在OA上,点E,F在扇形的弧上.问:哪种方案的正方形CDEF的面积更大?请说明理由. 20. 用一张长12cm宽5cm的矩形纸片折出一个菱形.小颖同学按照取两组对边中点的方法折出菱形EFGH(方案一),小丰同学沿矩形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB的方法得到菱形AECF(方案二).谁折出的菱形面积更大?请你通过计算说明.
20. 用一张长12cm宽5cm的矩形纸片折出一个菱形.小颖同学按照取两组对边中点的方法折出菱形EFGH(方案一),小丰同学沿矩形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB的方法得到菱形AECF(方案二).谁折出的菱形面积更大?请你通过计算说明.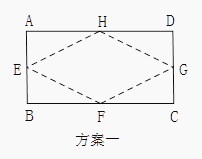
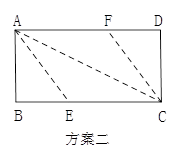
21. 为了充分利用四边形余料,小明设计了不同的方案裁剪正方形,裁剪方案与数据如表:方案设计
方案1
方案2
裁剪方案示意图


说明
图中的正方形AEFG和正方形MNPO四个顶点都在原四边形的边上
测量数据
AD=9dm,CD=2dm,AB=14dm,∠A=∠D=90°;
(1)、任务1:探寻边角 填空:BC=dm;sinB=;(2)、任务2:比较面积 计算或推理:正方形AEFG和正方形MNP边长之比;(3)、任务3:应用实践 若在△BEF余料上再截取一个最大正方形,正方形的边长为dm.22. 为了充分利用四边形余料,小明设计了不同的方案裁剪正方形,裁剪方案与数据如下表:方案设计
方案1
方案2
裁剪方案示意图


说明
图中的正方形和正方形四个顶点都在原四边形的边上
测量数据
, , , ;
任务1:探寻边角
填空: ▲ , ▲ ;
任务2:比较面积
计算或推理:正方形和正方形边长之比;
任务3:应用实践
若在余料上再截取一个最大正方形,正方形的边长为 ▲ .
23. 【问题背景】如图1,数学实践课上,学习小组进行探究活动,老师要求大家对矩形进行如下操作:①分别以点为圆心,以大于的长度为半径作弧,两弧相交于点 , , 作直线交于点 , 连接;②将沿翻折,点的对应点落在点处,作射线交于点 .

【问题提出】
在矩形中, , 求线段的长.
【问题解决】
经过小组合作、探究、展示,其中的两个方案如下:
方案一:连接 , 如图2.经过推理、计算可求出线段的长;
方案二:将绕点旋转至处,如图3.经过推理、计算可求出线段的长.
请你任选其中一种方案求线段的长.
七、新考法-回归教材,注重定理的证明
-
24. 【温故知新】在证明“三角形的中位线平行于第三边,且等于第三边的一半”时,小明结合图1给出如下证明思路:作交的延长线于点 , 再证 , 再证四边形是平行四边形,即可证明定理。

图1 图2 图3 图4
(1)、【新知体验】小明思考后发现:作平行线可以构成全等三角形或平行四边形,以达到解决问题的目的.如图2,在四边形中, , , 若 , , , 则的值为(2)、【灵活运用】如图3,在矩形和中,连接、交于点 , 连接。若 , 求的度数;(3)、【拓展延伸】如图4在第(2)题的条件下,连接 , 若 , 求的面积25. 【教材呈现】如图是华师版九年级上册数学教材第77页的部分内容:如图,在△ABC中,点D、E分别是AB与AC的中点,
可以猜想:DE//BC且DE=BC.
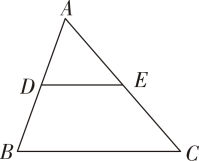

【定理证明】请根据教材内容,结合图①,写出证明过程.
(1)、如图②,四边形ABCD 中,AD= BC,E、F、G分别是AB、DC、AC的中点,若∠ACB=80°,∠DAC=20°,直接写出LEFG的度数.
(2)、如图③,在矩形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G,H分别是EC,FD 的中点,连接GH,若AB=6,BC=10,直接写出GH的长度.26. 【教材呈现】下图是华师版九年级上册数学教材第77页的部分内容.猜想
如图23.4.2,在中,点D、E分别是AB与AC的中点.根据画出的图形,可以猜想:
, 且 .
对此,我们可以用演绎推理给出证明.

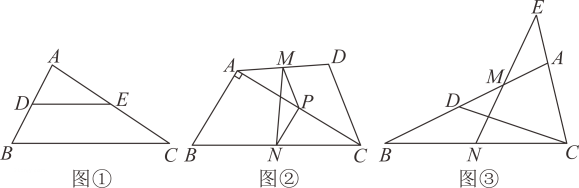
【定理证明】(1)、请根据教材提示,结合图①,写出完整的证明过程.(2)、如图②,在四边形ABCD中, , , 点P、M、N分别是AC、AD、BC的中点,连结PM、PN、MN.若 , 则的大小为;(3)、如图③,在中,点D在AB上,且 , 点M、N分别是AD、BC的中点,连结NM并延长,交CA延长线于点E,则与的数量关系为 .27. 课本再现思考
我们知道,菱形的对角线互相垂直.反过来,对角线互相垂直的平行四边形是菱形吗?
可以发现并证明菱形的一个判定定理:
对角线互相垂直的平行四边形是菱形.
 (1)、【定理证明】为了证明该定理,小明同学画出了图形(如图①),并写出了“已知”和“求证”,请你完成证明过程.
(1)、【定理证明】为了证明该定理,小明同学画出了图形(如图①),并写出了“已知”和“求证”,请你完成证明过程.已知:在中,对角线 , 垂足为.
求证:是菱形.
(2)、【知识应用】如图②,在中,对角线AC和BD相交于点.①求证:是菱形;
②延长BC至点 , 连接OE交CD于点 , 若 , 求的值.
28. 【教材呈现】下图是华师版八年级下册数学教材第83页和84页的部分内容.平行四边形的判定定理2 一组对边平行且相等的四边形是平行四边形.
我们可以用演绎推理证明这一结论.
已知:如图,在四边形中,ABCD且 .
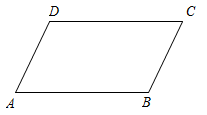
求证:四边形是平行四边形.
证明:连接 .
(1)、请根据教材提示,结合图,写出完整的证明过程.(2)、【知识应用】如图①,在中,延长到点 , 使 , 连接、 . 求证:四边形是平行四边形.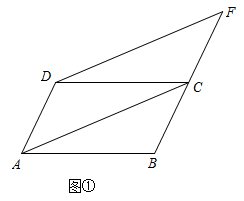 (3)、【拓展提升】在【知识应用】的条件下,若四边形的面积为7,直接写出四边形的面积.
(3)、【拓展提升】在【知识应用】的条件下,若四边形的面积为7,直接写出四边形的面积.八、新考法-纠错反思
-
29. 【题目】如图①,在矩形ABCD中, , F是AB延长线上一点,且 , 连结DF,交BC于点E,连结AE.试判断线段AE与DF的位置关系.

【探究展示】小明发现, , 并展示了如下的证明方法:
证明:∵ ,
∴ .
∵ ,
∴ .
∵四边形ABCD是矩形,
∴ .
∴ .
∵ ,
∴ .
∴ .
∵ ,
∴ . (依据)
(1)、【反思交流】上述证明过程中的“依据”是 .(2)、小颖受到小明的启发,继续进行探究,如图②,连结图①中的 , 将绕着点顺时针旋转得到 , 连结 . 求证:点在线段的垂直平分线上.(3)、【拓展应用】如图③,将图①中的绕着点顺时针旋转得到 . 分别以点、为圆心,以长为半径作弧,两弧交于点 , 连结 . 若 , 直接写出的值.九、新考法-真实问题情景
-
30. 综合与实践:
问题情境:数学课上,小广和小都两位同学利用三角板操作探究图形的旋转问题.
 (1)、操作探究:小广将两块全等的含角的直角三角板按如图①方式在平面内放置,其中两锐角顶点重合于点 , , 已知长 , 则点、之间的距离为 .(2)、操作探究:小都将两块全等的含角的直角三角板按如图②方式在平面内放置.
(1)、操作探究:小广将两块全等的含角的直角三角板按如图①方式在平面内放置,其中两锐角顶点重合于点 , , 已知长 , 则点、之间的距离为 .(2)、操作探究:小都将两块全等的含角的直角三角板按如图②方式在平面内放置.其中两个角顶点重合于点 , 与重合,已知长 , 请你帮小都同学求出此时点、之间的距离;
(3)、操作探究:随后,小将图②中的换成了含角的三角板,同相是顶点重合于点 , 与重合,已知直角边与长均为 , 他还想求点 , 之间距离,小广提出,如果把三角板也换成了含角的三角板,并利用旋转的知识,结论将更容易得到,你能求出此时点 , 之间的距离吗?
-