2024年中考数学考前20天终极冲刺专题之线段最值(一)
试卷更新日期:2024-05-21 类型:三轮冲刺
一、选择题
-
1. 如图,是线段上一点,和是位于直线同侧的两个等边三角形,点分别是的中点.若 , 则下列结论错误的是( )
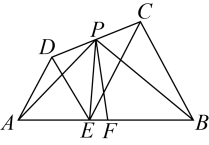 A、的最小值为 B、的最小值为 C、周长的最小值为6 D、四边形面积的最小值为2. 如图,已知直线分别交轴、轴于点B、A两点, , D、E分别为线段和线段上一动点,交轴于点 , 且 . 当的值最小时,则点的坐标为( )
A、的最小值为 B、的最小值为 C、周长的最小值为6 D、四边形面积的最小值为2. 如图,已知直线分别交轴、轴于点B、A两点, , D、E分别为线段和线段上一动点,交轴于点 , 且 . 当的值最小时,则点的坐标为( ) A、 B、 C、 D、3. 如图,在扇形中,平分交于点 , 点为半径上一动点.若 , 则阴影部分周长的最小值为( )
A、 B、 C、 D、3. 如图,在扇形中,平分交于点 , 点为半径上一动点.若 , 则阴影部分周长的最小值为( )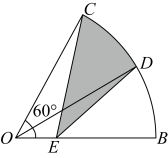 A、 B、 C、 D、4. 如图,直角三角形顶点在矩形的对角线上运动,连接 . , , , 则的最小值为( ).
A、 B、 C、 D、4. 如图,直角三角形顶点在矩形的对角线上运动,连接 . , , , 则的最小值为( ). A、 B、 C、 D、5. 如图,在中, , , , 的半径为1,点P是边上的动点,过点即P作的一条切线(点Q为切点),则切线长的最小值是( )
A、 B、 C、 D、5. 如图,在中, , , , 的半径为1,点P是边上的动点,过点即P作的一条切线(点Q为切点),则切线长的最小值是( ) A、 B、3 C、 D、46. 如图,∠AOB=30°,点M,N分别是OA,OB上的动点,P为∠AOB内一点,且OP=6,当△PMN的周长取最小值时,MN的长为( )
A、 B、3 C、 D、46. 如图,∠AOB=30°,点M,N分别是OA,OB上的动点,P为∠AOB内一点,且OP=6,当△PMN的周长取最小值时,MN的长为( ) A、6 B、12-18 C、18-18 D、127. 如图,在四边形刚好是中点,P、Q分别是线段上的动点,则的最小值为( )
A、6 B、12-18 C、18-18 D、127. 如图,在四边形刚好是中点,P、Q分别是线段上的动点,则的最小值为( ) A、12 B、15 C、16 D、188. 如图:等边三角形中, , 、分别是边、上的动点,且 , 则的最小值为( )
A、12 B、15 C、16 D、188. 如图:等边三角形中, , 、分别是边、上的动点,且 , 则的最小值为( ) A、 B、 C、 D、9. 如图,在边长为10的正方形对角线上有E,F两个动点,且 , 点P是中点,连接 , 则最小值为( )
A、 B、 C、 D、9. 如图,在边长为10的正方形对角线上有E,F两个动点,且 , 点P是中点,连接 , 则最小值为( ) A、 B、 C、 D、1010. 如图,在矩形中, , , 点在上,点在上,且 , 连接 , , 则的最小值为( )
A、 B、 C、 D、1010. 如图,在矩形中, , , 点在上,点在上,且 , 连接 , , 则的最小值为( ) A、 B、 C、 D、11. 如图,在中, , , , 点E在边BC上,并且 , 点F为边AC上的动点,将沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )
A、 B、 C、 D、11. 如图,在中, , , , 点E在边BC上,并且 , 点F为边AC上的动点,将沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )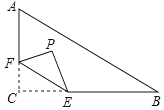 A、 B、1 C、2 D、12. 如图,正方形 的面积为 , 是等边三角形,点 在正方形 内,在对角线 上有一点 ,使 的和最小,则这个最小值为( ).
A、 B、1 C、2 D、12. 如图,正方形 的面积为 , 是等边三角形,点 在正方形 内,在对角线 上有一点 ,使 的和最小,则这个最小值为( ).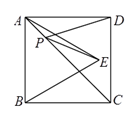 A、 B、 C、 D、13. 如图:点在轴上,是轴上的动点,将线段绕点逆时针旋转得线段 , 则长的最小值为( )
A、 B、 C、 D、13. 如图:点在轴上,是轴上的动点,将线段绕点逆时针旋转得线段 , 则长的最小值为( ) A、 B、 C、 D、14. 如图,中, , , 于点 , 若点是线段上一动点,则的最小值为( )
A、 B、 C、 D、14. 如图,中, , , 于点 , 若点是线段上一动点,则的最小值为( ) A、 B、 C、 D、15. 如图,在正方形ABCD中,E是边AD中点,F是边AB上一动点,G是EF延长线上一点,且GF=EF . 若AD=4,则EG2+CG2的最小值为( )
A、 B、 C、 D、15. 如图,在正方形ABCD中,E是边AD中点,F是边AB上一动点,G是EF延长线上一点,且GF=EF . 若AD=4,则EG2+CG2的最小值为( ) A、52 B、60 C、68 D、7616. 如图,在中,P为平面内的一点,连接 , 若 , 则的最小值是( )
A、52 B、60 C、68 D、7616. 如图,在中,P为平面内的一点,连接 , 若 , 则的最小值是( ) A、 B、36 C、 D、
A、 B、36 C、 D、二、填空题
-
17. 如图,在矩形中,为的中点,若为边上的两个动点,且 , 则线段的最小值为 .
 18. 如图,在直角坐标系中,已知点 , 点为轴正半轴上一动点,连接 , 以为一边向下作等边 , 连接 , 则的最小值为 .
18. 如图,在直角坐标系中,已知点 , 点为轴正半轴上一动点,连接 , 以为一边向下作等边 , 连接 , 则的最小值为 . 19. 如图,正方形ABCD的边长为12,⊙B的半径为6,点P是⊙B上一个动点,则的最小值为.
19. 如图,正方形ABCD的边长为12,⊙B的半径为6,点P是⊙B上一个动点,则的最小值为. 20. 如图,中, , 点为边上的中点,为边上的两个动点,且 , 则五边形的周长最小值为
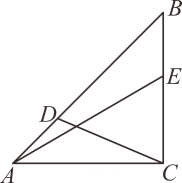
20. 如图,中, , 点为边上的中点,为边上的两个动点,且 , 则五边形的周长最小值为 21. 如图,在边长为6的等边△ABC中,点E,F分别是边AC,BC上的动点,且AE=CF,连接BE,AF交于点P,连接CP,则CP的最小值为 .
21. 如图,在边长为6的等边△ABC中,点E,F分别是边AC,BC上的动点,且AE=CF,连接BE,AF交于点P,连接CP,则CP的最小值为 . 22. 如图,在△ABC中,∠C=60°,AC=5,BC=4,点D为CB延长线上一点.当点D在CB延长线上运动时,AD-BD的最小值为 .
22. 如图,在△ABC中,∠C=60°,AC=5,BC=4,点D为CB延长线上一点.当点D在CB延长线上运动时,AD-BD的最小值为 . 23. 如图,已知点坐标为 , 为轴正半轴上一动点,则度数为 , 在点运动的过程中的最小值为 .
23. 如图,已知点坐标为 , 为轴正半轴上一动点,则度数为 , 在点运动的过程中的最小值为 .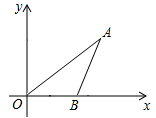 24. 如图,矩形ABCD中,AB=1,BC=2,AE为∠BAD的平分线,F为AE上一动点,点M为DF的中点,连接BM,则BM的最小值是.
24. 如图,矩形ABCD中,AB=1,BC=2,AE为∠BAD的平分线,F为AE上一动点,点M为DF的中点,连接BM,则BM的最小值是. 25. 如图,已知直线与x轴、y轴分别交于A、B两点,点P是以为圆心,1为半径的圆上一动点,连接 . 则面积的最大值与最小值的差为 .
25. 如图,已知直线与x轴、y轴分别交于A、B两点,点P是以为圆心,1为半径的圆上一动点,连接 . 则面积的最大值与最小值的差为 . 26. 如图,CD为等腰的高,其中 , E , F分别为线段CD , AC上的动点,且 , 当取最小值时,的度数为 .
26. 如图,CD为等腰的高,其中 , E , F分别为线段CD , AC上的动点,且 , 当取最小值时,的度数为 . 27. 如图,正方形的边长为8,点为边上一点,且 , 点为边上的一个动点,连接 , 以为一条直角边向右侧作等腰 , 且使 , 连接 , 则的最小值是 .
27. 如图,正方形的边长为8,点为边上一点,且 , 点为边上的一个动点,连接 , 以为一条直角边向右侧作等腰 , 且使 , 连接 , 则的最小值是 .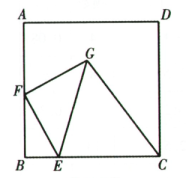
三、解答题
-
28. 数学课上,老师给出题目:如图所示,在中 , , 点D , E分别是边和边上的动点,且 , 连接 , . 请探究是否存在最小值?并说明理由.
嘉淇的想法是把和转移到某处,并使它们“接在一起”,然后利用“两点之间,线段最短”尝试探索,并成功解决了问题.以下是她的探索思路,请你按要求补充具体解题过程.
 (1)、在射线上取点F , 使 , 把绕点A顺时针旋转,使点D落在点F处,点C落在点G处.
(1)、在射线上取点F , 使 , 把绕点A顺时针旋转,使点D落在点F处,点C落在点G处.①请你运用尺规作图(保留作图痕迹,不用给出证明),作出 , 并连接;
②求证: .
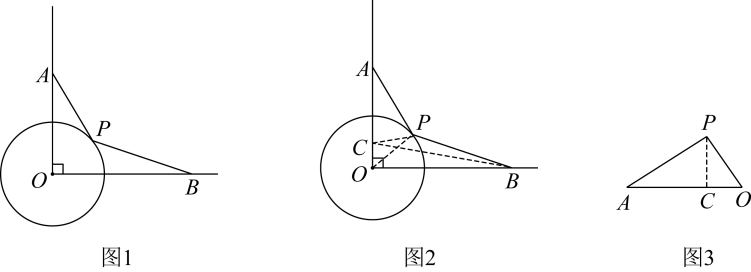
(2)、在(1)的基础上,请你通过探索,求出的最小值,并直接写出此时的长度.29.【问题呈现】如图1,∠AOB=90°, OA=4,OB=5,点P在半径为2的⊙O上,求的最小值.
【问题解决】小明是这样做的:如图2,在OA上取一点C使得OC=1,这样可得 , 又因为∠COP=∠POA,所以可得△COP ∽△POA,所以 , 得所以.
又因为 , 所以最小值为 ▲ .
【思路点拨】小明通过构造相似形(图3),将转化成CP,再利用“两点之间线段”最短”求出CP+ BP的最小值.
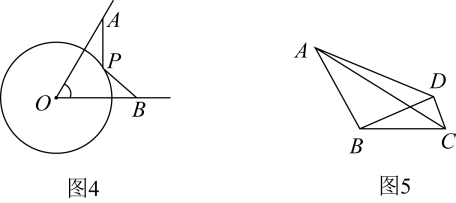
【尝试应用】如图4,∠AOB=60°, OA=10,OB=9,点P是半径为6的⊙O上一动点,求的最小值.
【能力提升】如图5,∠ABC=120°, BA= BC=8,点D为平面内一点且BD= 3CD,连接AD,则△ABD面积的最大值为 ▲ .
四、实践探究题
-
30. 【阅读材料】说明代数式的几何意义,并求它的最小值.
解: , 如图1,建立平面直角坐标系,点P(x,0)是x轴上一点,则可以看成点P与点A(0,1)的距离,可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是求PA+PB的最小值.
设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,所以PA′+PB的最小值为线段A′B的长度.为此,构造直角三角形A′CB,因为A′C=3,CB=3,所以 , 即原式的最小值为 .

根据以上阅读材料,解答下列问题:
(1)、【基础训练】代数式的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B 的距离之和;(填写点B的坐标)(2)、【能力提升】求代数式的最小值为 ;(3)、【拓展升华】如图2,在等腰直角△ABC中,∠BAC=90°,点M,N分别为BC,AC上的动点,且 . 当AM+BN的值最小时,求CM的长.