2024年中考数学考前20天终极冲刺专题之圆(一)
试卷更新日期:2024-05-21 类型:三轮冲刺
一、选择题
-
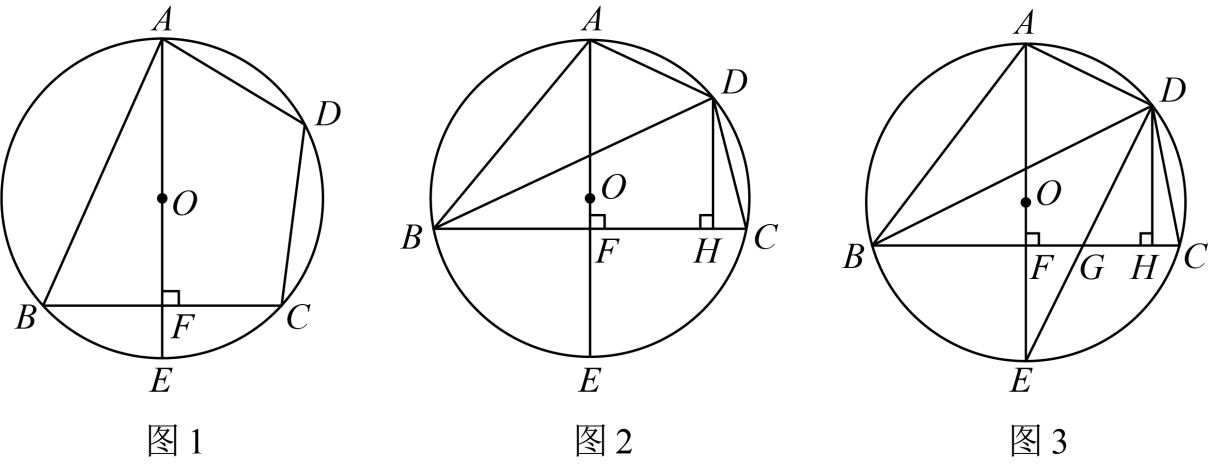
1. 如图,是半圆O的直径,C、D、E三点依次在半圆O上,若 , , 则与之间的关系是( )
 A、 B、 C、 D、2. 如图,是半圆的直径,点在半圆上, , 连接 , 过点作 , 交的延长线于点 . 设的面积为的面积为 , 若 , 则的值为( )
A、 B、 C、 D、2. 如图,是半圆的直径,点在半圆上, , 连接 , 过点作 , 交的延长线于点 . 设的面积为的面积为 , 若 , 则的值为( )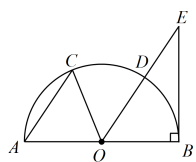 A、 B、 C、 D、3. 赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为 , 拱高约为 , 则赵州桥主桥拱半径R约为( )
A、 B、 C、 D、3. 赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为 , 拱高约为 , 则赵州桥主桥拱半径R约为( )
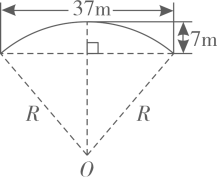 A、 B、 C、 D、4. 如图,四边形ABCD是⊙O的内接四边形,若∠ABC=114°,则∠AOC的度数为( )
A、 B、 C、 D、4. 如图,四边形ABCD是⊙O的内接四边形,若∠ABC=114°,则∠AOC的度数为( ) A、134° B、132° C、76° D、66°5. 如图,AB是⊙O的直径,弦CD⊥AB于点E , 在BC上取点F , 使得CF=CE , 连结AF交CD于点G , 连结AD . 若CG=GF , 则的值等于( )
A、134° B、132° C、76° D、66°5. 如图,AB是⊙O的直径,弦CD⊥AB于点E , 在BC上取点F , 使得CF=CE , 连结AF交CD于点G , 连结AD . 若CG=GF , 则的值等于( ) A、 B、 C、 D、6. 如图,为的直径,将沿翻折,翻折后的弧交于D.若 , , 则图中阴影部分的面积为( )
A、 B、 C、 D、6. 如图,为的直径,将沿翻折,翻折后的弧交于D.若 , , 则图中阴影部分的面积为( ) A、 B、 C、8 D、107. 如图,正方形的边长为4,点是边上的一点,将沿着折叠至 , 若、恰好与正方形的中心为圆心的相切,则折痕的长为( )
A、 B、 C、8 D、107. 如图,正方形的边长为4,点是边上的一点,将沿着折叠至 , 若、恰好与正方形的中心为圆心的相切,则折痕的长为( ) A、 B、5 C、 D、以上都不对8. 如图,AD是的外角平分线,与的外接圆交于点 , 连结BD交AC于点 , 且 , 则下列结论错误的是( )
A、 B、5 C、 D、以上都不对8. 如图,AD是的外角平分线,与的外接圆交于点 , 连结BD交AC于点 , 且 , 则下列结论错误的是( ) A、 B、 C、 D、9. 如图,的圆心M在一次函数位于第一象限中的图象上,与y轴交于C、D两点,若与x轴相切,且 , 则半径是( )
A、 B、 C、 D、9. 如图,的圆心M在一次函数位于第一象限中的图象上,与y轴交于C、D两点,若与x轴相切,且 , 则半径是( ) A、或5 B、5或6 C、或6 D、510. 如图,等边三角形ABC内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边三角形ABC的内心成中心对称,则圆中的黑色部分的面积与△ABC的面积之比是( )
A、或5 B、5或6 C、或6 D、510. 如图,等边三角形ABC内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边三角形ABC的内心成中心对称,则圆中的黑色部分的面积与△ABC的面积之比是( )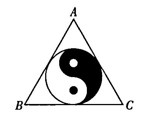 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,四边形是的内接四边形,对角线相交于点 , 且 , 过点作交延长线于点 . 若 . 则的面积为
 12. 如图,在平面直角坐标系中,点 , , 的坐标分别为 , , , 点是三角形的外接圆上一点,交线段于点 , 若 , 则点的坐标为.
12. 如图,在平面直角坐标系中,点 , , 的坐标分别为 , , , 点是三角形的外接圆上一点,交线段于点 , 若 , 则点的坐标为. 13. 已知:是的外接圆,是的直径,的平分线交于点 , 过点作 , 垂足为点
13. 已知:是的外接圆,是的直径,的平分线交于点 , 过点作 , 垂足为点① , ,则
②若 , 则 ;
 14. 如图,内接于 , 已知是直径, , , 点D在直径上方的半圆上运动,连接交于点E , 则的长度为 , 的最大值为 .
14. 如图,内接于 , 已知是直径, , , 点D在直径上方的半圆上运动,连接交于点E , 则的长度为 , 的最大值为 . 15. 如图,在由10个完全相同的正三角形构成的网格图中,∠α、∠β如图所示,则sin(α+β)= .
15. 如图,在由10个完全相同的正三角形构成的网格图中,∠α、∠β如图所示,则sin(α+β)= . 16. 如图,在扇形AOB中,点C,D在上,将D沿弦折叠后恰好与OA,OB相切于点E,F.已知∠AOB=120°,OA=6,则的度数为 , 折痕CD的长为.
16. 如图,在扇形AOB中,点C,D在上,将D沿弦折叠后恰好与OA,OB相切于点E,F.已知∠AOB=120°,OA=6,则的度数为 , 折痕CD的长为.
三、解答题
-
17. 如图,在中, , 以为直径作 , 交于点 , 连接并延长,分别交于两点,连接 .
 (1)、求证:是的切线;(2)、求证:;(3)、求的正切值.18. 如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D , 连接BD、CD , 过点D作BC的平行线与AC的延长线相交于点P .
(1)、求证:是的切线;(2)、求证:;(3)、求的正切值.18. 如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D , 连接BD、CD , 过点D作BC的平行线与AC的延长线相交于点P . (1)、求证:PD是⊙O的切线;(2)、求证:△ABD∽△DCP;(3)、当AB=12,AC=16时,求CD和DP的长.19. 如图,直线AB经过⊙O上的点C , 并且OA=OB , CA=CB , 直线OB交⊙O于点E、D , 连接EC、CD .
(1)、求证:PD是⊙O的切线;(2)、求证:△ABD∽△DCP;(3)、当AB=12,AC=16时,求CD和DP的长.19. 如图,直线AB经过⊙O上的点C , 并且OA=OB , CA=CB , 直线OB交⊙O于点E、D , 连接EC、CD .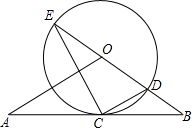 (1)、试判断直线AB与⊙O的位置关系,并加以证明;(2)、求证:;(3)、若 , ⊙O的半径为3,求OA的长.20. 如图1,将的顶点C放在上,边与相切于点C , 边与交于点D . 已知 , , , 的直径为8.
(1)、试判断直线AB与⊙O的位置关系,并加以证明;(2)、求证:;(3)、若 , ⊙O的半径为3,求OA的长.20. 如图1,将的顶点C放在上,边与相切于点C , 边与交于点D . 已知 , , , 的直径为8. (1)、如图1,过点O作于点M , 求的长度;(2)、从图1的位置开始,将绕点C顺时针旋转,设旋转角为().
(1)、如图1,过点O作于点M , 求的长度;(2)、从图1的位置开始,将绕点C顺时针旋转,设旋转角为().①如图2,当时,边与的另一交点为E , 求的长度;
②如图3,当经过圆心O时,试判断与之间的位置关系,并说明理由;
③在旋转过程中,直接写出点O到边的距离h的取值范围.