浙江省嘉兴市桐乡六中教育集团2023-2024学年七年级（下）月考数学试卷（3月份）

试卷更新日期：2024-05-21 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10题，每小题3分，共30分）

1. 下列方程组中，是二元一次方程组的是（）

A、 ${\begin{matrix} 3 x^{2} + y = 1 \\ 10 x - 8 y = - 9 \end{matrix}$ B、 ${\begin{matrix} x y = 4 \\ x + 2 y = 6 \end{matrix}$ C、 ${\begin{matrix} x - y = 2 \\ \frac{1}{x} - 3 y = - \frac{7}{4} \end{matrix}$ D、 ${\begin{matrix} x + 2 y = 4 \\ 7 x - 9 y = 5 \end{matrix}$

查看试题解析
2. $∠ 1$ 与 $∠ 2$ 是同位角， $∠ 1 = 70 °$ ，则 $∠ 2 =$ （）

A、70° B、110° C、20° D、不能确定

查看试题解析
3. 如图，直线 $a$ ， $b$ 被直线 $c$ 所截，则 $∠ 1$ 的同旁内角是（）

A、 $∠ 2$ B、 $∠ 3$ C、 $∠ 4$ D、 $∠ 5$

查看试题解析
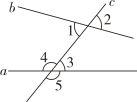4. 方程组 $\{\begin{array}{l} y = 2 x - 5 \\ 3 x - 2 y = 8 \end{array}$ 用代入法消去y后所得的方程是（　　）

A、3x﹣4x﹣10＝8 B、3x﹣4x+5＝8 C、3x﹣4x﹣5＝8 D、3x﹣4x+10＝8

查看试题解析
5. 方程2x+y=8的正整数解的个数是（　　）

A、4 B、3 C、2 D、1

查看试题解析
6. 如图，在下列条件中，能判断AB∥CD的是（　　）

A、∠1＝∠2 B、∠BAD＝∠BCD C、∠3＝∠4 D、∠BAD+∠ADC＝180°

查看试题解析
7. 下列计算正确的是（　　）

A、x²·x⁴＝x⁸ B、（﹣2⁸）³＝（﹣2）²⁴ C、（3cd）³＝9c³d³ D、（x³）²＝x⁶

查看试题解析
8. 将如图①的矩形ABCD纸片沿EF折叠得到图②，折叠后DE与BF相交于点P ，如果∠BPE＝130°，则∠PEF的度数为（　　）

A、60° B、65° C、70° D、75°

查看试题解析
9. 如图， $A B ∥ E F$ ， $∠ A B P = \frac{1}{4} ∠ A B C$ ， $∠ E F P = \frac{1}{4} ∠ E F C$ ，已知 $∠ F C D = 60 °$ ，则 $∠ P$ 的度数为（）

A、58° B、60° C、62° D、64°

查看试题解析
10. 已知关于x ， y的方程组 ${\begin{array}{l} x + y = a + 4, \\ x - 2 y = 4 a - 2, \end{array}$ 给出下列结论：
①当 $a = 3$ 时，方程组的解也是 $x + y = 2 a + 1$ 的解；②无论a取何值，x ， y的值不可能是互为相反数；③x ， y都为自然数的解有4对；④若 $2 x + y = 9$ ，则 $a = 1$ ．
正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共6题，每小题3分，共18分）

11. 已知方程3x﹣y＝5，用含x的代数式表示y ，则．

查看试题解析
12. 已知（m﹣1）x+y^|^m^|＝4是关于x、y二元一次方程，则m＝．

查看试题解析
13. 若a^x•a³＝（a²）³ ，则x＝．

查看试题解析
14. 如图，面积为12cm²的三角形ABC沿BC方向平移到三角形DEF的位置，平移的距离是边长BC长的2倍，则图中四边形ACED的面积为 cm² ．

查看试题解析
15. 欢欢观察“抖空竹”时发现，可以将某一时刻的情形抽象成数学问题：如图，已知AB∥CD，∠BAE＝92°，∠DCE＝115°，则∠E的度数是°．

查看试题解析
16. 三个同学对问题“若方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 的解是 ${\begin{array}{l} x = 5 \\ y = 6 \end{array}$ ，求方程组 ${\begin{array}{l} 5 a_{1} x + 3 b_{1} y = 4 c_{1} \\ 5 a_{2} x + 3 b_{2} y = 4 c_{2} \end{array}$ 的解”提出各自的想法．甲说：“这个题目好像条件不够，不能求解”；乙说：“它们的系数有一定的规律，这可以试试”；丙说：“能不能通过换元替代的方法来解决”，参照他们的讨论，你认为这个题目的解应该是．

查看试题解析

三、解答题（本大题共有8小题，17-22每题6分，23、24每题8分，共52分）

17. 计算：

(1)、（﹣2a³）³；

(2)、﹣p²•（﹣p）⁴•（﹣p）⁵ ．

查看试题解析
18. 解方程组．

(1)、 ${\begin{matrix} x = 2 y \\ 3 x - 2 y = 8 \end{matrix}$

(2)、 ${\begin{matrix} 3 x - 5 y = 8 \\ 6 x + 7 y = - 1 \end{matrix}$ ．

查看试题解析
19.
如图：在正方形网格中有一个△ABC，按要求进行下列作图（只借助于网格，需写出结论）：

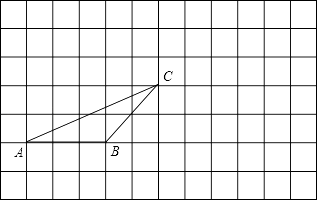(1)、过点A画出BC的平行线；

(2)、画出先将△ABC向右平移5格，再向上平移3格后的△DEF；

查看试题解析
20. 已知：如图， $∠ A B D = 100 °$ ，且BC平分 $∠ A B D$ ， $∠ 1 = 50 °$ ．

(1)、求证： $A B ∥ C D$ ．

(2)、求证： $∠ 2$ 的度数．

查看试题解析
21. 如图，在大长方形ABCD中，放入六个相同的小长方形，已知 $B C = 11$ ， $D E = 7$ ．

(1)、设每个小长方形的长为x ，宽为y ，求x ， y的值．

(2)、求图中阴影部分的面积．

查看试题解析
22. 某校准备组织七年级340名学生参加北京夏令营，已知用3辆小客车和1辆大客车每次可运送学生105人；用1辆小客车和2辆大客车每次可运送学生110人；

(1)、每辆小客车和每辆大客车各能坐多少名学生？

(2)、若学校计划租用小客车x辆，大客车y辆，一次送完，且恰好每辆车都坐满；
①请你设计出所有的租车方案；
②若小客车每辆需租金4000元，大客车每辆需租金8000元，请选出最省钱的租车方案，并求出最少租金．

查看试题解析
23. 阅读感悟：
有些关于方程组的问题，需要求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题：
已知实数x ， y满足3x﹣y＝5①，2x+3y＝7②，求x﹣4y和7x+5y的值．
本题常规思路是将①②两式联立组成方程组，解得x ， y的值再代入欲求值的代数式得到答案，常规思路运算量比较大．其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由①﹣②可得x﹣4y＝﹣2，由①+②×2可得7x+5y＝19．这样的解题思想就是通常所说的“整体思想”．
解决问题：

(1)、已知二元一次方程组 $\{\begin{array}{l} 2 x + 3 y = 17 \\ 3 x + 2 y = 13 \end{array}$ ，则x﹣y＝， x+y＝；

(2)、对于实数x ， y ，定义新运算：x*y＝ax﹣by+c ，其中a ， b ， c是常数，等式右边是通常的加法和乘法运算．已知3*5＝15，4*7＝28，那么求1*1的值．

查看试题解析
24. 如图，已知直线AB∥CD ， E ， F分别是AB ， CD上的点，点G在直线AB ， CD内部，且∠AEG＝30°，∠CFG＝45°．

(1)、求∠EGF的度数．

(2)、如图2，射线EG绕点E以每秒5°的速度逆时针旋转，交直线CD于点P ，设运动时间为t秒（0＜t＜30）．当t＝21时，试探究EP与GF的位置关系，并说明理由．

(3)、在（2）中，射线FG绕点F同时以每秒10°的速度顺时针旋转得到射线FQ ．当FQ∥EP时，请直接写出t的值．

查看试题解析