广东省汕头市濠江区2024年中考数学一模试题

试卷更新日期：2024-05-21 类型：中考模拟

进入出卷网下载

一、选择题（本大题10题，每小题3分，共30分）．在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．

1. 给出四个数0， $- \frac{1}{2}$ ， $- 2$ ， 2024，其中最小的是（）

A、0 B、 $- \frac{1}{2}$ C、 $- 2$ D、2024

查看试题解析
2. 某几何体的三视图如图所示，则此几何体是（）

A、 B、 C、 D、

查看试题解析
3. 阅读可以丰富知识，拓展视野，在世界读书日（4月23日）当天，某校为了解学生的课外阅读，随机调查了40名学生课外阅读册数的情况，现将调查结果绘制成如图．关于学生的读书册数，下列描述正确的是（　　）

A、极差是6 B、中位数是5 C、众数是6 D、平均数是5

查看试题解析
4. 计算 $2^{4} + 2^{4} = 2^{?}$ ，则“？”是（）

A、4 B、5 C、6 D、8

查看试题解析
5. 一元一次不等式组 ${\begin{array}{l} 3 x + 4 \geq 1 \\ 5 - 2 x > - 1 \end{array}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则一次函数 $y = b x + c$ 与反比例函数 $y = \frac{a + b}{x}$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
7. 如图， $B C$ 是 $⊙ O$ 的切线，点B是切点，延长 $C O$ 交 $⊙ O$ 于点A ，连接 $A B$ ， $O D = 2$ ， $∠ C = 30 °$ ，则 $A B$ 的长为（）

A、 $2 \sqrt{2}$ B、 $2 \sqrt{3}$ C、 $3 \sqrt{2}$ D、 $3 \sqrt{3}$

查看试题解析
8. 四边形 $A B C D$ 中， $A B / / C D$ ，且 $A B$ ， $C D$ 长是关于x的方程 $x^{2} - 3 m x + 2 m^{2} + m - 2 = 0$ 的两个实数根，则四边形 $A B C D$ 是（）

A、梯形 B、矩形 C、平行四边形 D、平行四边形或梯形

查看试题解析
9. 为降低成本，某出租车公司推出了“油改气”措施，如图， $y_{1}$ ， $y_{2}$ 分别表示燃油汽车和燃气汽车行驶路程S（单位：千米）与所需费用y（单位：元）的关系，已知燃油汽车每千米所需的费用比燃气汽车每千米所需费用2倍多0.2元，设燃气汽车每千米所需费用为x元，则可列方程为（）

A、 $\frac{30}{x} = \frac{10}{2 x - 0.2}$ B、 $\frac{30}{x} = \frac{10}{2 x - 0.2}$ C、 $\frac{30}{2 x + 0.2} = \frac{10}{x}$ D、 $\frac{30}{x} = \frac{10}{2 x + 0.2}$

查看试题解析
10. 用弹管秤将一长方体铁块悬于没有盛水的水槽中，再向水槽匀速注入水，直至铁块完全浸没在水中（如图），则能反映弹簧秤的读数y（单位：N）与水面高度x（单位： $c m$ ）之间的函数关系的大致图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题（本大题6题，每小题3分，共18分）．请将下列各题的正确答案填写在答题卡相应的位置上．

11. 据探测，马里亚纳海沟的最大水深位于斐查兹海渊，水深约11000米，是地球的最深点，11000用科学记数法表示为．

查看试题解析
12. 若点 $(x_{1}, y_{1})$ ， $(x_{2}, y_{2})$ 都在反比例函数 $y = \frac{2024}{x}$ 的图象上，且 $x_{1} < 0 < x_{2}$ ，则 $y_{1}$ $y_{2}$ ．（填“ $>$ ”“ $<$ ”或“ $=$ ”）

查看试题解析
13. 某校课后服务课程有：足球，篮球，书法，舞蹈．为了解最受学生喜爱的课后服务课程，该校对初一同学进行调查，并将调查结果绘制成两幅不完整的统计图（如图），该校初一学生中最喜爱足球课程的人数是．

查看试题解析
14. 若边长分别为a ， b（ $a < b$ ）的两个正方形按如图所示摆放，则图中阴影部分的面积为．（用含a ， b的式子表示）

查看试题解析
15. 如图，在 $Rt △ ABC$ 中， $∠ ACB = 90 °$ ， $AC = 9$ ， $BC = 12$ ， $AB = 15$ ， $AD$ 是 $∠ BAC$ 的平分线，若点 $P$ 、 $Q$ 分别是 $AD$ 和 $AC$ 上的动点，则 $PC + PQ$ 的最小值是．

查看试题解析
16. 已知正方形 $M N K O$ 和正六边形 $A B C D E F$ 边长均为1，把正方形放在正六边形外边，使 $O K$ 边与 $A B$ 边重合，如图所示，按下列步骤操作：将正方形在正六边形外绕点B顺时针旋转，使 $K N$ 边与 $B C$ 边重合，完成第一次旅转；再绕点C顺时针旋转，使 $N M$ 边与 $C D$ 边重合，完成第二次旋转；…在这样连续的旋转过程中，第6次点M在图中直角坐标系中的坐标是．

查看试题解析

三、解答题（本大题共9小题，满分72分．解答应写出文字说明、证明过程或演算步骤．）

17. 计算： $(π - 2024)^{0} - 2 t a n 45 ° + | - 2 | + \sqrt{9}$

查看试题解析
18. 如图，点C为 $∠ A O B$ 平分线上一点， $C D / / O B$ 交 $O A$ 于点D ．求证： $△ D O C$ 是等腰三角形．

查看试题解析
19.

(1)、如图 $4 \times 4$ 的方格，每个小格的顶点叫做格点，若每个小正方形边长为1单位，请在方格中作一个正方形，同时满足下列两个条件：
①所作的正方形的顶点，必须在方格上；
②所作正方形的面积为8个平方单位；

(2)、在数轴上表示实数 $\sqrt{8}$ （保留作图痕迹）

查看试题解析
20. 阅读材料：运用公式法分解因式，除了常用的平方差公式和完全平方公式以外，还可以应用其他公式，如立方和与立方差公式，其公式如下：
立方和公式： $x^{3} + y^{3} = (x + y) (x^{2} - x y + y^{2})$ ；
立方差公式： $x^{3} - y^{3} = (x - y) (x^{2} + x y + y^{2})$ .
根据材料和已学知识解决下列问题

(1)、因式分解： $a^{3} - 8$ ；

(2)、先化简，再求值： $(\frac{3 x}{x^{2} - 2 x} - \frac{x^{2} + 2 x + 4}{x^{3} - 8}) \div \frac{2}{x^{2} - 4}$ ，其中 $x = 3$ .

查看试题解析
21. 嘉嘉给琪琪展示她做的一个小程序，如图，运行程序后屏幕显示一个平面直角坐标系，当她在键盘上输入数字“2”时，屏幕上显示一个点，坐标为 $(2 ， 0)$ ，输入数字“3”时，屏幕上显示另一个点，坐标为 $(3 ， - 3)$ ，嘉嘉告诉琪琪：这些点都在抛物线 $y = a x^{2} + b x$ 上．

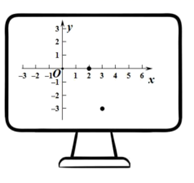(1)、求抛物线的解析式，并求出输入“4”得到的点的坐标；

(2)、嘉嘉和琪琪从2、3、4中各选一个数字输入，得到两个不同的点，求两个点都在 $x$ 轴下方的概率．

查看试题解析
22. 甲、乙两家草莓采摘园的草莓品质相同，销售价格也相同．“五一”假期，两家均推出了优惠方案，甲采摘园的优惠方案：游客进园需购买60元的门票，采摘的草莓六折优惠；乙采摘园的优惠方案：游客进园不需购买门票，采摘的草莓超过一定数量后，超过部分打折优惠．优惠期间，设某游客的草莓采摘量为x（千克），在甲采摘园所需总费用为 $y_{甲}$ （元），在乙采摘园所需总费用为 $y_{乙}$ （元），图中折线 $O - A - B$ 表示 $y_{乙}$ 与x之间的函数关系．

(1)、求 $y_{甲}$ 、 $y_{乙}$ 与x之间的函数关系式；

(2)、当游客采摘15千克的草莓时，你认为他在哪家草莓园采摘更划算？

查看试题解析
23. 如图，⊙O是△ABC的外接圆，AD是⊙O的直径，F是AD延长线上一点，连接CD，CF，且CF是⊙O的切线．

(1)、求证：∠DCF＝∠CAD．

(2)、探究线段CF，FD，FA的数量关系并说明理由；

(3)、若cosB＝ $\frac{3}{5}$ ， AD＝2，求FD的长．

查看试题解析
24. 如图，二次函数的图象与x轴交于点 $A (- 6, 0)$ 和点B ，与y轴交于点C ，且顶点D的坐标为 $(- 2, 8)$ ，对称轴与直线 $A C$ 交于点E ，与x轴交于点F ，连接 $A C$ ， $B C$ ．

(1)、求二次函数的解析式；

(2)、点P在 $A C$ 上方二次函数图象上，且 $△ P D E$ 的面积等于6，求点P的坐标；

(3)、在二次函数图象上是否存在一点M ，使得 $∠ A C M + ∠ O C B = 45 °$ ？若存在，求出直线 $C M$ 与x轴的交点Q的坐标；若不存在，请说明理由．

查看试题解析
25. 如图①，在矩形 $A B C D$ 中， $A B = 8$ ， $A D = 10$ ， E是 $C D$ 边上一点，连接 $A E$ ，将矩形 $A B C D$ 沿 $A E$ 折叠，顶点D恰好落在 $B C$ 边上点F处，延长 $A E$ 交 $B C$ 的延长线于点G ．

(1)、求线段 $C E$ 的长．

(2)、判断四边形 $A F G D$ 是什么特殊四边形，并说明理由．

(3)、如图②，M、N分别是线段 $A G$ ， $D G$ 上的动点（与端点不重合），且 $∠ D M N = ∠ D A M$ ，设 $D N = x$ ．是否存在这样的点N ，使 $△ D M N$ 是直角三角形？若存在，请求出x的值；若不存在，请说明理由．

查看试题解析