广西东兴市2024年春七年级下学期数学（3月）月考考试试卷

试卷更新日期：2024-05-21 类型：月考试卷

进入出卷网下载

一、单选题（本题共计12小题，总分48分）

1. 16 的平方根是( )

A、4 B、—4 C、±2 D、±4

查看试题解析
2. 下面四个图形中， $∠ 1 = ∠ 2$ 一定成立的是( 　　)

A、 B、 C、 D、

查看试题解析
3. 下列说法正确的是（　　）

A、-4的平方根是±2 B、-4的算术平方根是-2 C、 $\sqrt{16}$ 的平方根是±4 D、0的平方根与算术平方根都是0

查看试题解析
4. 估计 $\sqrt{13}$ 的值在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
5. 如图，若 $a ∥ b$ ， $∠ 1 = 60 °$ ，则 $∠ 2$ 的度数是( 　)

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $120 °$

查看试题解析
6. 将一块直角三角板与两边平行的纸条如图放置，若 $∠ 1 = 55 °$ ，则 $∠ 2$ =(　　)

A、35° B、45° C、55° D、65°

查看试题解析
7. 下列说法正确的是( )

A、过一点有且只有一条直线与已知直线平行 B、垂直于同一条直线的两条直线互相平行 C、从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离 D、在平面内过一点有且只有一条直线与已知直线垂直

查看试题解析
8. 如果一个角的两边与另一个角的两边互相垂直，那么这两个角的关系为(　　).

A、互补 B、相等 C、相等或互余 D、相等或互补

查看试题解析
9. 如图，直线AB∥CD ， AE⊥CE于点E ，若∠EAB＝120°，则∠ECD的度数是(　　)

A、120° B、100° C、150° D、160°

查看试题解析
10. 如图，将Rt△ABC沿着BC的方向平移到Rt△DEF的位置，已知AB=5，DO=2，平移距离为3，则阴影部分的面积为( )

A、12 B、24 C、21 D、20.5

查看试题解析
11. 如图，直线 l₁∥l₂ ， ∠α=∠β，∠1=50°，则∠2的度数为（）

A、130° B、120° C、115° D、100°

查看试题解析
12. 如果 $∠ A$ 与 $∠ B$ 的两边分别平行， $∠ A$ 比 $∠ B$ 的3倍少36°，则 $∠ A$ =( )

A、 $1 8^{\circ}$ B、 $12 6^{\circ}$ C、 $1 8^{\circ}$ 或 $12 6^{\circ}$ D、以上都不对

查看试题解析

二、填空题（本题共计8小题，总分32分）

13. 4的算术平方根是．

查看试题解析
14. 已知x ， y为实数，且 $\sqrt{x + 1} + {(y - 2)}^{2} = 0$ ，则y—x=.

查看试题解析
15. 如图，下列条件：① $∠ B + ∠ B C D = 180 °$ ；② $∠ 1 = ∠ 2$ ；③ $∠ 3 = ∠ 4$ ；④ $∠ B = ∠ 5$ ；⑤ $∠ B = ∠ D$ .其中，一定能判定 $A B$ ∥ $C D$ 的条件有(填写所序号).

查看试题解析
16. 如图，在直角三角形ABC中，∠A=90°，AB=3cm，AC=4cm，BC=5cm，则点A到边BC的距离是.

查看试题解析
17. 在同一平面内，设a、b、c是三条互相平行的直线，已知a与b的距离为5，b与c的距离为2，则a与c的距离为.

查看试题解析
18. 如图，若∠AOB与∠BOC是一对邻补角，OD平分∠AOB，在∠BOC内部，并且∠BOE= $\frac{1}{2}$ ∠COE，∠DOE=70°，则∠COE的度数是.

查看试题解析
19. 如图，将一个长方形纸片ABCD沿EF折叠，点C恰好落在AD边上点G处，点D落在点H处.若∠CFE＝72°，则∠EGH的度数为.

查看试题解析
20. 如图， $A B ∥ C D$ ， E为 $A B$ 上一点，且 $E F ⊥ C D$ 垂足为F ， $∠ C E D = 90 °$ ， $C E$ 平分 $∠ A E G$ ，且 $∠ C G E = α$ ，则下列结论：① $∠ A E C = 90 ° - \frac{1}{2} α$ ；② $D E$ 平分 $∠ G E B$ ；③ $∠ C E F = ∠ G E D$ ；④ $∠ F E D + ∠ B E C = 180 °$ ；其中正确的有.(请填写序号)

查看试题解析

三、解答题（本题共计7小题，总分70分）

21. 下列式子中x的值.

(1)、 $x^{2} = 49 ；$

(2)、 $4 (x — 1)^{2} = 169 ；$

查看试题解析
22. 如图，平原上有A，B，C，D四个村庄，为解决当地缺水问题，政府准备投资修建一个蓄水池.

(1)、请你画图确定蓄水池H点的位置，使它到四个村庄距离之和最小；

(2)、计划把河水引入蓄水池H中，怎样开渠最短并说明根据.(画图后说明依据)

查看试题解析
23. 一个正数的两个平方根是 $x + 6$ 与 $2 x - 9$ ，求这个正数.

查看试题解析
24. 如图， $A B ⊥ B F, C D ⊥ B F, ∠ 1 = ∠ 2$ ，试说明 $∠ 3 = ∠ E$ .
证明：∵ $A B ⊥ B F, C D ⊥ B F$ (已知)
∴ $∠ A B D = ∠$      ▲  =90 $°$ (垂直定义)
∴     ▲  //     ▲  (         )
∵ $∠ 1 = ∠ 2$ (         )
∴     ▲  //     ▲  (         )
∴ $C D / /$      ▲  _(平行于同一直线的两条直线互相平行)
∴ $∠ 3 = ∠ E$ (         ).

查看试题解析
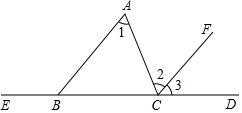
25. 如图，已知∠1＝∠2，∠3＝50°，求∠ABE的度数．

查看试题解析
26. 如图，AD⊥BC于点D ， EG⊥BC于点G ， ∠E＝∠3，
求证：AD平分∠BAC.

查看试题解析
27. 问题情景：已知直线AB∥CD ，点E在AB、CD之间，点P、Q分别在直线AB、CD上，连接PE、EQ.

(1)、如图1，过点E作EH∥AB ，运用上述结论，探究∠PEQ、∠APE、∠CQE之间的数量关系，并说明理由；

(2)、如图2，类比(1)中的方法，运用上述结论，探究∠PEQ、∠APE、∠CQE之间的数量关系，并说明理由；

(3)、如图3，PF平分∠BPE ， QF平分∠EQD ，当∠PEQ＝140°时，直接写出∠PFQ的度数.

查看试题解析

广西东兴市2024年春七年级下学期数学（3月）月考考试试卷

一、 单选题 （本题共计12小题，总分48分）

二、 填空题 （本题共计8小题，总分32分）

三、 解答题 （本题共计7小题，总分70分）

一、单选题（本题共计12小题，总分48分）

二、填空题（本题共计8小题，总分32分）

三、解答题（本题共计7小题，总分70分）