辽宁省大连市金普新区2022-2023学年七年级下学期数学4月月考试卷
试卷更新日期:2024-05-21 类型:月考试卷
一、选择题(每题2分,共20分)
-
1. 如图,∠1和∠2是对顶角的图形是( )A、
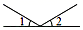 B、
B、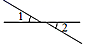 C、
C、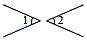 D、
D、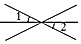 2. 9的算术平方根是( )A、3 B、 C、 D、3. 如图, , 若 , 则的度数是( )
2. 9的算术平方根是( )A、3 B、 C、 D、3. 如图, , 若 , 则的度数是( ) A、 B、 C、 D、4. 在下列各组数中,互为相反数的是( )A、与 B、与 C、与 D、3与5. 点在第( )象限.A、第一象限 B、第二象限 C、第三象限 D、第四象限6.
A、 B、 C、 D、4. 在下列各组数中,互为相反数的是( )A、与 B、与 C、与 D、3与5. 点在第( )象限.A、第一象限 B、第二象限 C、第三象限 D、第四象限6.如图,在△ABC 中,∠C=90°.若BD∥AE,∠DBC=20°,则∠CAE的度数是 ( )
 A、40° B、60° C、70° D、80°7. 下列各式表示正确的是( )A、 B、 C、 D、8. 下列实数中,有理数有( )个.A、1 B、2 C、3 D、49. 如图所示, ,垂足分别为A、D,已知 ,则点A到线段 的距离是( )
A、40° B、60° C、70° D、80°7. 下列各式表示正确的是( )A、 B、 C、 D、8. 下列实数中,有理数有( )个.A、1 B、2 C、3 D、49. 如图所示, ,垂足分别为A、D,已知 ,则点A到线段 的距离是( ) A、10 B、8 C、6 D、4.810. 如图,把一张对边互相平行的纸条沿折叠,若 , 则下列结论:①;②;③;④ . 其中正确的有( )
A、10 B、8 C、6 D、4.810. 如图,把一张对边互相平行的纸条沿折叠,若 , 则下列结论:①;②;③;④ . 其中正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每空3分,共18分)
-
11. 3的平方根是12. 如图,是的平分线,交于点 . 若 , 则的度数为。
 13. 计算的值是。14. 如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短.
13. 计算的值是。14. 如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短.理由是.
 15. 已知直角坐标系中,点满足 . 则点坐标为。16. 如图,若AB∥CD,则α,β,γ之间的关系为
15. 已知直角坐标系中,点满足 . 则点坐标为。16. 如图,若AB∥CD,则α,β,γ之间的关系为
三、解答题(第17每小题4分,共8分,第18、19题各8分,共24分)
-
17. 计算:(1)、;(2)、 .18. 求下列各式中未知数的值:(1)、;(2)、 .19. 若一个正数的平方根是和 , 求这个数.
四、解答题(每小题8分,共16分)
-
20. 请把下列证明过程补充完整:
已知:如图, .

求证: .
证明:因为(已知),
所以 ▲ ( ),
因为(已知),
所以 ▲ ( ).
因为(已知),
所以( ),
即 ▲
所以 ▲ (等量代换),
所以( ).
21. 如图,将△ABC向左平移6个单位长度,再向下平移4个单位长度,可以得到△A1B1C1 , 画出平移后的△A1B1C1
①直接写出△A1B1C1各个顶点的坐标;
②写出S△ABC= ▲ .
五、解答题(本题8分)
-
22. 如图,用两个面积为的小正方形纸片剪拼成一个大的正方形.
 (1)、大正方形的边长;(2)、请你探究是否能将此大正方形纸片沿着边的方向裁出一个面积为的长方形纸片,使它的长宽之比为 , 若能,求出这个长方形纸片的长和宽,若不能,请说明理由.
(1)、大正方形的边长;(2)、请你探究是否能将此大正方形纸片沿着边的方向裁出一个面积为的长方形纸片,使它的长宽之比为 , 若能,求出这个长方形纸片的长和宽,若不能,请说明理由.六、解答题(本题10分)
-
23. 如图,已知上一点 , 且平分 .
 (1)、求的度数;(2)、试说明射线平分 .
(1)、求的度数;(2)、试说明射线平分 .七、解答题(本题12分)
-
24. 阅读下面的文字,解答问题:大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,的整数部分是1,将这个数减去其整数部分,差就是小数部分,的小数部分是 . 又例如: , 即的整数部分为2,小数部分为 .(1)、如果的整数部分为的小数部分为 , 则 , ;(2)、已知的小数部分为的小数部分为 , 求的值;(3)、若 , 其中是整数,且 , 求的相反数.
八、(本题12分)
-
25. 已知:如图,直线 , 直线分别与交于两点,点是直线上一点,点是上一点,连接 .
 (1)、点分别在射线上,当时,
(1)、点分别在射线上,当时,①试判断与的位置关系,并说明理由;
②若射线平分 , 求的度数.
(2)、点分别在射线 , 直线上时,请你在备用图中画出满足条件的图形,写出此时与的关系,并说明理由.
-
-
-