辽宁省葫芦岛市2024学年九年级下学期数学一模试卷
试卷更新日期:2024-05-21 类型:中考模拟
一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数,如果收入50元记作元,那么元表示( )A、支出20元 B、收入20元 C、支出30元 D、收入30元2. 如图是由6个完全相同的小正方体组成的几何体,则从左面看得到的平面图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
3. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 若关于的一元二次方程有两个实数根,则的取值范围是( )A、 B、 C、且 D、且6. 不等式组的解集在数轴上可表示为( ).A、
4. 下列运算正确的是( )A、 B、 C、 D、5. 若关于的一元二次方程有两个实数根,则的取值范围是( )A、 B、 C、且 D、且6. 不等式组的解集在数轴上可表示为( ).A、 B、
B、 C、
C、 D、
D、 7. 已知一次函数的图象如图所示,则下列判断中正确的是( )
7. 已知一次函数的图象如图所示,则下列判断中正确的是( ) A、 B、方程的解是 C、当时, D、随的增大而减小8. 《九章算术》是我国古代重要的数学专著之一,其中记录的一道题译为白话文是:把一份文件慢马送到900-里外的城市,需要的时间比规定时间多1天;如果用快马送,所需的时间比规定时间少3天.已知快马的速度是慢马的2倍,求规定时间.设规定时间为天,则可列方程为( )A、 B、 C、 D、9. 如图,直线 , 点在上, , 垂足为 . 若 , 则度数为( )
A、 B、方程的解是 C、当时, D、随的增大而减小8. 《九章算术》是我国古代重要的数学专著之一,其中记录的一道题译为白话文是:把一份文件慢马送到900-里外的城市,需要的时间比规定时间多1天;如果用快马送,所需的时间比规定时间少3天.已知快马的速度是慢马的2倍,求规定时间.设规定时间为天,则可列方程为( )A、 B、 C、 D、9. 如图,直线 , 点在上, , 垂足为 . 若 , 则度数为( ) A、 B、 C、 D、10. 如图,矩形中, , 以点B为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线 , 过点C作的垂线分别交于点M,N,则的长为( )
A、 B、 C、 D、10. 如图,矩形中, , 以点B为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线 , 过点C作的垂线分别交于点M,N,则的长为( )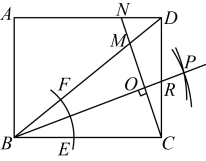 A、 B、 C、 D、4
A、 B、 C、 D、4二、填空题(本题共5小题;每小题3分,共15分)
-
11. 若a,b为两个连续整数,且 , 则.12. 如图,网格上的小正方形边长均为1,和的顶点都在格点上.若是由向右平移个单位,再向下平移个单位得到的,则的值为 .
 13. 有四张完全一样正面分别写有汉字“清”“风”“朗”“月”的卡片,将其背面朝上并洗匀,从中随机抽取一张,记下卡片正面上的汉字后放回,洗匀后再从中随机抽取一张,则抽取的两张卡片上的汉字相同的概率是 .14. 如图,矩形的顶点的坐标分别是 , 反比例函数的图像经过顶点边交轴于点 , 若四边形的面积等于面积的5倍,则的值等于 .
13. 有四张完全一样正面分别写有汉字“清”“风”“朗”“月”的卡片,将其背面朝上并洗匀,从中随机抽取一张,记下卡片正面上的汉字后放回,洗匀后再从中随机抽取一张,则抽取的两张卡片上的汉字相同的概率是 .14. 如图,矩形的顶点的坐标分别是 , 反比例函数的图像经过顶点边交轴于点 , 若四边形的面积等于面积的5倍,则的值等于 . 15. 如图,在中,为斜边的中点,是边上的一个动点,将沿翻折得到 , 当直线与垂直时,的长为 .
15. 如图,在中,为斜边的中点,是边上的一个动点,将沿翻折得到 , 当直线与垂直时,的长为 .
三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)
-
16. 计算(1)、;(2)、 .17. 新学期开始了,同学们将走出教室进行适当的体育锻炼,某校9.1班想集体购买跳绳和毽子,已知购买2条跳绳和3个毽子,需花费26元,购买1条跳绳和4个毽子,需花费18元.(1)、求跳绳和毽子的单价各是多少元?(2)、经商谈,商家给予9.1班购买一条跳绳即赠送一个毽子的优惠,如果9.1班需要毽子的数量是跳绳数量的2倍还多8个,且该班级购买跳绳和毽子的总费用不超过260元,那么该班级最多可购买多少条跳绳?18. 某校八年级共有男生300人,为了解该年级男生“排球垫球成绩”和“掷实心球成绩”的情况,从中随机抽取若干名男生进行这两项测试,对数据进行整理、描述和分析,下面是给出的部分信息.
信息一:排球垫球成绩如图(不完整)所示(成绩用x表示,单位:个.分成六组:
A、;B、;C、;D、;E、;F、).

信息二:排球垫球成绩在D、这一组的是:20,20,21,21,21,22,22,23,24,24;
信息三:掷实心球成绩(成绩用表示,单位:米)的人数(频数)分布表如表:
分组
人数
2
10
9
6
2
信息四:这次抽样测试中6名男生的两项成绩的部分数据如表:
学生
学生1
学生2
学生3
学生4
学生5
学生6
排球垫球(个)
26
25
23
22
22
15
掸实心球(米)
▲
7.8
7.8
▲
8.8
9.2
根据以上信息,回答下列问题:
(1)、求出被随机抽取的男生人数,并补全条形统计图:(2)、下列结论正确的是;(填序号)①;
②排球垫球成绩超过10个的人数占抽取人数的百分比低于;
③掷实心球成绩的中位数记为 , 则;
④若排球垫球成绩达到22个及以上时,成绩记为优秀,如果信息四中6名男生的两项成绩恰好为优秀的有4名,那么学生3掷实心球的成绩是优秀;
(3)、若排球垫球成绩达到22个及以上时,成绩记为优秀,请估计全年级男生排球垫球成绩达到优秀的人数.19. 小强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水,甲壶比乙壶加热速度快.在=段时间内,“水温y(℃)与加热时间x(s)之间近似满足一次函数关系,根据记录的数据,画函数图象如下: (1)、求乙壶中水温y关于加热时间x的函数解析式;(2)、当甲壶中水温刚达到80℃时,求此刻乙壶中水的温度?20. 塔山阻击战革命烈士纪念碑(图1)位于葫芦岛市区以东12公里的连山区塔山乡塔山村,是“全国爱国主义教育示范基地”.某校“综合与实践”活动小组借助无人机测量纪念碑主碑的高度.如图2,先将无人机升至距离地面10米高的点处,测得主碑最高点的仰角为 , 再将无人机从点处竖直向上升高至距离地面15.8米高的点处,测得点的俯角为 , 已知点在同一平面内,求纪念碑主碑的高度.(结果精确到0.1米)
(1)、求乙壶中水温y关于加热时间x的函数解析式;(2)、当甲壶中水温刚达到80℃时,求此刻乙壶中水的温度?20. 塔山阻击战革命烈士纪念碑(图1)位于葫芦岛市区以东12公里的连山区塔山乡塔山村,是“全国爱国主义教育示范基地”.某校“综合与实践”活动小组借助无人机测量纪念碑主碑的高度.如图2,先将无人机升至距离地面10米高的点处,测得主碑最高点的仰角为 , 再将无人机从点处竖直向上升高至距离地面15.8米高的点处,测得点的俯角为 , 已知点在同一平面内,求纪念碑主碑的高度.(结果精确到0.1米)(参考数据:)
 21. 如图,内接于为的直径,弦平分 , 交于点 , 以为邻边作平行四边形 , 延长交延长线于点 .
21. 如图,内接于为的直径,弦平分 , 交于点 , 以为邻边作平行四边形 , 延长交延长线于点 . (1)、求证:与相切;(2)、若 , 求的长.22. 跳台滑雪是冬季奥运会的比赛项目之一,运动员通过助滑道后在点处起跳经空中飞行后落在着陆坡上某处,他在空中飞行的路线可以看作抛物线的一部分.如图是跳台滑雪训练场横截面示意图,这里表示起跳点到地面的距离, , 以为坐标原点,以地面的水平线为轴,所在的直线为轴,建立平面直角坐标系.某运动员在处起跳腾空后,在空中飞行过程中,运动员到轴的距离与水平方向移动的距离满足 . 在着陆坡上设置点作为基准点,点与相距 , 高度(与距离)为 , 着陆点在点或超过点视为成绩达标.
(1)、求证:与相切;(2)、若 , 求的长.22. 跳台滑雪是冬季奥运会的比赛项目之一,运动员通过助滑道后在点处起跳经空中飞行后落在着陆坡上某处,他在空中飞行的路线可以看作抛物线的一部分.如图是跳台滑雪训练场横截面示意图,这里表示起跳点到地面的距离, , 以为坐标原点,以地面的水平线为轴,所在的直线为轴,建立平面直角坐标系.某运动员在处起跳腾空后,在空中飞行过程中,运动员到轴的距离与水平方向移动的距离满足 . 在着陆坡上设置点作为基准点,点与相距 , 高度(与距离)为 , 着陆点在点或超过点视为成绩达标. (1)、若某运动员在一次试跳中飞行的水平距离为时,恰好达到最大高度,试判断他的这次试跳落地点能否达标,说明理由;(2)、研究发现,运动员的运动轨迹与清出速度的大小有关,下表是某运动员7次试跳的与的对应数据:
(1)、若某运动员在一次试跳中飞行的水平距离为时,恰好达到最大高度,试判断他的这次试跳落地点能否达标,说明理由;(2)、研究发现,运动员的运动轨迹与清出速度的大小有关,下表是某运动员7次试跳的与的对应数据:150
170
190
210
230
250
270
①猜想关于的函数类型,求函数解析式,并任选一对对应值验证;
②当滑出速度为多少时,运动员的成绩刚好能达标?
23.(1)、【问题初探】如图1,是的中线,交于点 , 交于点 , 且 , 求证: .
小明和小亮两名同学从不同角度进行思考,给出了两种解题思路.

①小明同学的思考过程:如图2,延长到点 , 使 , 连接 , 构造……;
②小亮同学的解题思路与小明基本一致,也是构造三角形,只是构造方法不同.如图3,过点作交延长线于点G , 于是得到……;请你选择一名同学的解题思路,写出解答过程.
(2)、【迁移应用】请你依照上述两名同学的解题思路或者按照自己的思路,解答下面问题.如图4,已知等边中,为边上一动点,连接 , 将绕着顺时针旋转120°得到 , 连接 , 取中点 , 连接 , 猜想与的数量关系,并证明你的猜想;
 (3)、【能力提升】
(3)、【能力提升】如图5,已知中, , 点是斜边上的一点,且 , 连接 , 将线段绕点顺时针旋转 , 得到线段 , 连接线段 , 点为线段的中点,连接 . 若 , 求线段的长度.