辽宁省鞍山市岫岩满族自治县2023-2024学年七年级下学期数学4月月考试卷

试卷更新日期：2024-05-21 类型：月考试卷

进入出卷网下载

一、选择题（本题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一选项是符合题目要求的）

1. 4的算术平方根是（）

A、 $\pm 2$ B、2 C、4 D、 $- 2$

查看试题解析
2. 下列图形中，∠1与∠2不是同位角的是（）

A、 B、 C、 D、

查看试题解析
3. 下列命题中，正确的是（）

A、在同一平面内，垂直于同一条直线的两条直线平行 B、相等的角是对顶角 C、两条直线被第三条直线所截，同位角相等 D、和为180°的两个角叫相邻补角

查看试题解析
4. 如图，能判定EC∥AB的条件是（）

A、∠B＝∠ACE B、∠A＝∠ECD C、∠B＝∠ACB D、∠A＝∠ACE

查看试题解析
5. $a - 1$ 与 $3 - 2 a$ 是某正数的两个平方根，则实数a的值是（）

A、4 B、 $- \frac{4}{3}$ C、2 D、 $- 2$

查看试题解析
6. 估算 $\sqrt{27} - 2$ 的值（）

A、在1到2之间 B、在2到3之间 C、在3到4之间 D、在4到5之间

查看试题解析
7. 如图所示， $A B ∥ C D$ ，则正确的是（）

A、 $∠ A + ∠ C = 180 °$ B、 $∠ B + ∠ A = 180 °$ C、 $∠ B + ∠ D = 180 °$ D、 $∠ B + ∠ C = 180 °$

查看试题解析
8. 如图，一辆汽车经过两次拐弯后，行驶方向与原来平行，若第一次是向左拐30°，则第二次拐弯的角度是（）

A、右拐30° B、左拐30° C、左拐150° D、右拐150°

查看试题解析
9. 如图， $△ A B C$ 平移后得到 $△ D E F$ ，若 $A E = 11$ ， $D B = 5$ ，则平移的距离是（）

A、6 B、3 C、5 D、11

查看试题解析
10. 如图，直线 $A B ∥ C D$ ，点P在直线 $A B$ 、 $C D$ 之间，点E、Q分别在 $A B$ 、 $C D$ 上.连接 $P E$ 、 $P Q$ ， $∠ A E P < 90 °$ ， $E F$ 平分 $∠ P E B$ 交 $C D$ 于点F ， $P Q ∥ E F$ ， $∠ E P Q = 100 °$ ，则 $∠ C Q P$ 的度数是（）

A、80° B、70° C、60° D、50°

查看试题解析

二、填空题（本题共5小题，每小题3分，共15分）

11. 计算： $\sqrt{81}$ =

查看试题解析
12. $m + 1$ 是25的平方根，则m为.

查看试题解析
13. 把命题“对顶角相等”改写成“如果…那么…”的形式：

查看试题解析
14. 如图所示，某住宅小区内有一长方形地块，想在长方形地块内修筑同样宽的两条“之”字路，余下部分绿化，道路的宽为2米，则绿化的面积为 $m^{2}$ .

查看试题解析
15. 在同一平面内有2002条直线 $a_{1}$ ， $a_{2}$ ， …， $a_{2002}$ ，如果 $a_{1} ⊥ a_{2}$ ， $a_{2} ∥ a_{3}$ ， $a_{3} ⊥ a_{4}$ ， $a_{4} ∥ a_{5}$ ， …，那么 $a_{1}$ 与 $a_{2002}$ 的位置关系是.

查看试题解析

三、解答题（本题共8小题，共75分，解答应写出文字说明、演算步骤或推理过程）

16. 如图，直线 $A B$ 与直线 $C D$ 相交于点C ，根据下列语句画图：

(1)、过点P作 $C D$ 的平行线，交 $A B$ 于点Q；

(2)、过点P作 $A B$ 的垂线段，垂足为点H；

(3)、连接 $P C$ ；

(4)、填空：点P到直线 $A B$ 的距离是线段的长度；

(5)、比较线段的大小： $P C$ $P H$ （填 $>$ ， $<$ ， $\geq$ ， $\leq$ ）

查看试题解析
17. 已知a为 $\sqrt{170}$ 的整数部分， $b - 3$ 是400的算术平方根，求 $\sqrt{a + b}$ .

查看试题解析
18.

(1)、 $9 x^{2} - 25 = 0$

(2)、 $24 {(x - 1)}^{2} - 6 = 0$

查看试题解析
19. 如图，直线AB，CD相交于点O，EO⊥AB，垂足为O．

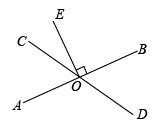(1)、若∠EOC＝35°，求∠AOD的度数；

(2)、若∠BOC＝2∠AOC，求∠DOE的度数．

查看试题解析
20. 请把下面证明过程补充完整
如图，已知 $A D ⊥ B C$ 于D ，点E在 $B A$ 的延长线上， $E G ⊥ B C$ 于G ，交 $A C$ 于点F ， $∠ E = ∠ 1$ .
求证： $A D$ 平分 $∠ B A C$ .
证明：∵ $A D ⊥ B C$ 于D ， $E G ⊥ B C$ 于G（已知），
∴ $∠ A D C = ∠ E G C = 90 °$ （），
∴ $A D ∥$ ▲ （），
∴ $∠ 1 = ∠ 2$ （），
▲ $= ∠ 3$ （），
又∵ $∠ E = ∠ 1$ （已知），
∴ $∠ 2 = ∠ 3$ （），
∴ $A D$ 平分 $∠ B A C$ （）.

查看试题解析
21. 如图所示是甲、乙二人在 $△ A B C$ 中的行进路线，甲： $B \to D \to F \to E$ ；乙： $B \to C \to E \to D$ .已知 $∠ 1 + ∠ 2 = 180 °$ ， $∠ 3 = ∠ B$ .

(1)、试判断 $∠ A E D$ 与 $∠ A C B$ 的大小关系，并说明理由；

(2)、直接写出有哪些路线是平行的?

查看试题解析
22.

(1)、如图， $D E ∥ B C$ ， $∠ 1 = ∠ 3$ ， $C D ⊥ A B$ ，试说明 $F G ⊥ A B$ ；

(2)、若把（1）中的题设中的“ $D E ∥ B C$ ”与结论“ $F G ⊥ A B$ ”对调，所得命题是否为真命题?试说明理由.

查看试题解析
23. 如图，直线 $A C ∥ B D$ ，连接 $A B$ ，直线 $A C$ 、 $B D$ 及线段 $A B$ 把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分.当动点P落在某个部分时，连接 $P A$ ， $P B$ ，构成 $∠ P A C$ ， $∠ A P B$ ， $∠ P B D$ 三个角.（提示：有公共端点的两条重合的射线所组成的角是0°角）

(1)、当动点P落在第①部分时，求证： $∠ A P B = ∠ P A C + ∠ P B D$ ；

(2)、当动点P落在第②部分时， $∠ A P B = ∠ P A C + ∠ P B D$ 是否成立?如果成立，请说明理由；不成立直接写出结论.

(3)、当动点P落在第③部分时，全面探究 $∠ P A C$ ， $∠ A P B$ ， $∠ P B D$ 之间的关系，并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明.

查看试题解析