广西河池市宜州区2024年九年级中考数学一模试题

试卷更新日期：2024-05-21 类型：中考模拟

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分。在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑）

1. 在世界数学史上首次正式引入负数的是中国古代著作《九章算术》．若某天中午的气温是 $4 ° C$ ，记作 $+ 4 ° C$ ，则当天晚上的气温零下 $5 ° C$ 可记作（）

A、 $- 5 ° C$ B、 $- 4 ° C$ C、 $+ 5 ° C$ D、 $+ 9 ° C$

查看试题解析
2. 水是生命之源，滋润着世间万物．国家节水标志由水滴、手掌和地球设计而成，寓意着要像对待掌上明珠一样，珍惜每一滴水．以下图形中，可以通过平移节水标志得到的是（）

A、 B、 C、 D、

查看试题解析
3. 下列几何体中，从正面看到的平面图形是圆的是（）

A、 B、 C、 D、

查看试题解析
4. 不等式 $2 x - 1 \leq 5$ 的解集是（）

A、 $x \leq 3$ B、 $x \geq 3$ C、 $x < 3$ D、 $x > 3$

查看试题解析
5. 把一把直尺与一块三角板按如图所示的方式放置，若 $∠ 1 = 42 °$ ，则 $∠ 2$ 的度数为（）

A、 $125 °$ B、 $120 °$ C、 $130 °$ D、 $132 °$

查看试题解析
6. 下列运算正确的是 $($ 　　 $)$

A、 $2 a + 3 b = 6 a b$ B、 $a^{2} \cdot a = a^{2}$ C、 $(a^{2})^{3} = a^{5}$ D、 $3 a^{3} \cdot (- 4 a^{2}) = - 12 a^{5}$

查看试题解析
7. 对甲、乙、丙、丁四名射击选手进行射击测试，每人射击10次，平均成绩均为9.5环，方差如表所示，则四名选手中成绩最稳定的是（）
选手
甲
乙
丙
丁
方差
1.34
0.16
2.56
0.21

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 已知一个扇形的圆心角为 $150 °$ ，半径是6，则这个扇形的面积是（）

A、 $15 π$ B、 $10 π$ C、 $5 π$ D、 $2.5 π$

查看试题解析
9. 2022年秋季学期某校学生平均每天书面作业时长为90分钟，在“双减”政策的推动下，经过2023年春季学期和2023年秋季学期两次调整后，2023年秋季学期平均每天书面作业时长为70分钟，设该校这两学期平均每天书面作业时长每学期的下降率为x ，则可列方程为（）

A、 $70 (1 + x^{2}) = 90$ B、 $70 (1 + x)^{2} = 90$ C、 $90 (1 - x^{2}) = 70$ D、 $90 (1 - x)^{2} = 70$

查看试题解析
10. 如图，△ABC≌△AED ，点E在线段BC上，∠1＝40°，则∠AED的度数是（）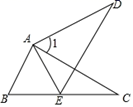

A、70° B、68° C、65° D、60°

查看试题解析
11. 宽与长的比是 $\frac{\sqrt{5} - 1}{2}$ 的矩形叫黄金矩形．心理测试表明：黄金矩形令人赏心悦目，它给我们以协调、匀称的美感．现在，按照如下的步骤作图（如图）：
第一步：作一个正方形ABCD；
第二步：分别取AD ， BC的中点M ， N ，连接MN；
第三步：以点N为圆心，ND长为半径画弧，交BC的延长线于点E；
第四步：过点E作 $E F ⊥ A D$ ，交AD的延长线于点F ．
则所作图形中是黄金矩形的为（）

A、矩形MNCD B、矩形DCEF C、矩形MNEF D、矩形DCEF和矩形ABEF

查看试题解析
12. 如图，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象与 $R t △ A O B$ 的直角边AB相交于点C ，直角顶点B在x轴上，交斜边AO于点D ．若 $A D : O D = 2 : 3$ ，且 $S_{△ O A C} = 16$ ，则k的值为（）

A、8 B、9 C、16 D、18

查看试题解析

二、填空题（本大题共6小题，每小题2分，共12分）

13. 要使式子 $\sqrt{x - 5}$ 有意义，则x应满足的条件是．

查看试题解析
14. 分解因式： $m^{2} - 4$ = ．

查看试题解析
15. 如图，AB为⊙O的直径，弦CD⊥AB于点E ，已知CD＝16，OE＝6，则⊙O的直径为．

查看试题解析
16. 谚语“八月十五云遮月，正月十五雪打灯”是说如果八月十五晚上阴天的话，正月十五晚上就下雪．你认为谚语说的是（填写“必然事件”或“不可能事件”或“随机事件”）

查看试题解析
17. 课外活动小组测量学校旗杆的高度．如图，当太阳光线与地面成 $30 °$ 角时，测得旗杆AB在地而上的影子BC的长为24米，那么旗杆AB的高度是米．（结果保留根号）

查看试题解析
18. 如图，直线 $y = 2 x + 1$ 与x轴交于点A ，与y轴交于点B ，将直线AB绕点B顺时针旋转 $45 °$ 与x轴交于点C ，则直线BC的解析式为．

查看试题解析

三、解答题（本大题共8小题，共72分。解答应写出文字说明、证明过程或演算步骤）

19. 计算： $(- 2)^{3} \div 4 - 5 \times (- 3)^{2}$ ．

查看试题解析
20. 解方： $x^{2} - 4 x - 3 = 0$ ．

查看试题解析
21. 如图，在 $△ A B C$ 中， $∠ B = 30 °, ∠ C = 90 °$ ，作线段AB的垂直平分线，交BC于点D ，交AB于点E ．

(1)、依题意补全图形，（要求：尺规作图，保留作图痕迹，不写作法）

(2)、求证： $C D = \frac{1}{2} B D$ 。

查看试题解析
22. 为全面增强中学生的体质，某学校开展“阳光体育活动”，开设了4门选修课：A．跳绳；B．篮球；C．排球；D．足球，要求每名学生必须选择其中的一项参加．全校共有100名男生选择了A项目，为了解选择A项目男生的情况，从这100名男生中随机抽取了30人进行测试，并将他们的成绩x（个/分钟）绘制成频数分布直方图．
选A项目男生的测试情况选择四个项目的男生在全校男生总人数所占百分比

(1)、若抽取的同学的测试成绩落在 $160 \leq x < 165$ 这一组的数据为160，162，161，163，162，164，则该组数据的中位数是，众数是；

(2)、根据题目信息，估计选择B项目的男生共有人，扇形统计图中D项目所占圆的圆心角为度；

(3)、学校准备选出甲、乙、丙、丁四名同学中的2名参加全区的跳绳比赛，请用画树状图法或列表法计算出甲和乙同学同时被选中的概率

查看试题解析
23. 骑车出行已经成为人们积极响应绿色出行的新风尚．图1是某品牌自行车放在水平地面上的示意图，图2是其简化版，其中 $A B ∥ C D ∥ l$ ，车轮半径为 $32 c m, ∠ A B C = 64 °, B C = 60 c m$ ，坐垫E到，点B的距离BE为 $10 c m$ ．
图1 图2

(1)、求坐垫E到地面的距离．

(2)、根据经验，当坐垫E到CD的距离调整为人体腿长的0.8倍时，骑车时会比较舒适．小明的腿长约为 $84 c m$ ，现将坐垫E调整至坐骑舒适高度位置 $E^{'}$ ，求 $E E^{'}$ 的长．（结果精确到 $0.1 c m$ ．参考数据： $s i n 64 ° \approx 0.90, c o s 64 ° \approx 0.44, t a n 64 ° \approx 2.05$ ）

查看试题解析
24. 如图，已知 $△ A B C$ 是边长为 $6 c m$ 的等边三角形，动点P ， Q同时从A、B两，点出发，分别沿AB、BC匀速运动，其中点P运动的速度是 $1 c m / s$ ，点Q运动的速度是 $2 c m / s$ ，当点Q到达点C时，P、Q两点都停止运动，设运动时间为 $t (s)$ ，
解答下列问题：

(1)、设 $△ B P Q$ 的面积为 $S (c m^{2})$ ，求S与t的函数关系式；

(2)、作 $Q R ∥ B A$ 交AC于点R ，连接PR ，当t为何值时， $△ A P R ∽ △ P R Q$ 。

查看试题解析
25. 某汽车制造厂接到同为生产360辆汽车的两项任务．

(1)、完成第一项任务时，第一天按原计划的生产效率进行，第一天后按原计划生产效率的1.5倍进行生产，结果提前3天完成任务．完成第一项任务实际需要多少天？

(2)、在完成第二项任务时，制造厂设计了甲、乙两种不同的生产方案（其中 $a \neq b$ ）．
甲方案：计划180辆按每天生产a辆完成，剩下的180辆按每天生产b辆完成，设完成生产任务所需的时间为 $t_{1}$ 天。
乙方案：设完成生产任务所需的时间为 $t_{2}$ 天，其中一半时间每天生产a辆，另一半时间每天生产b辆．
请比较 $t_{1}, t_{2}$ 的大小，并说明理由．

查看试题解析
26. 综合与实践
小赵同学在学习完“圆”这一章内容后，发现某些几何题目，通过添加辅助圆，运用圆的知识去解决，可以使问题变得容易．这个过程称为“化隐圆为显圆”。

(1)、【学习心得】这类题目主要是两种类型：
①“定点+定长”：如图1，在 $△ A B C$ 中， $A B = A C, ∠ B A C = 44 °$ ， D是 $△ A B C$ 外一点，且 $A D = A C$ ，求的度数．
解：若以点A（定点）为圆心，AB（定长）为半径作辅助圆 $⊙ A$ ，则点C ， D必在 $⊙ A$ 上， $∠ B A C$ 是 $⊙ A$ 中圆心角，而 $∠ B D C$ 是圆周角，从而可容易得到 $∠ B D C =$ ▲ ．
②“定角十定弦”：如图2，在 $R t △ A B C$ 中， $A B ⊥ B C, A B = 6, B C = 4$ ， P是 $△ A B C$ 内部的一个动点，且满足 $∠ P A B = ∠ P B C$ ，求线段CP长的最小值
解： $∵ ∠ A B C = 90 °, ∴ ∠ A B P + ∠ P B C = 90 °$ ．
$∵ ∠ P A B = ∠ P B C, ∴ ∠ B A P + ∠ A B P = 90 °$ ，
$∴ ∠ A P B =$ ▲ ，（定角）
$∴$ 点P在以AB(定弦)为直径的 $⊙ O$ 上。
请将以上解答的过程补充完整，

(2)、【问题解决】如图3，在矩形ABCD中，已知 $A B = 3, B C = 4$ ， P是BC边上一动点（点P不与点B ， C重合），连接AP ，作点B关于直线AP的对称点M ，则线段MC的最小值为．

(3)、【问题拓展】如图4，在正方形ABCD中， $A D = 4$ ，动点E ， F分别在边DC ， CB上移动，且满足 $D E = C F$ ．连接AE和DF ，交于点P ．
①写出AE与DF的数量关系和位置关系，并说明理由；
②点E从点D开始运动到点C时，点P也随之运动，请求出点P的运动路径长．

查看试题解析

选手	甲	乙	丙	丁
方差	1.34	0.16	2.56	0.21