广东省揭阳市普宁市2024年中考数学一模试题

试卷更新日期：2024-05-21 类型：中考模拟

进入出卷网下载

一、选择题（本大题10小题，每小题3分，共30分.在每小题列出的四个选项中，只有一个正确选项，请将正确答案写在答题卡的相应位置.）

1. 凝固点是晶体物质凝固时的温度，标准大气压下，下列物质中凝固点最低的是（　　）
物质钨水银煤油水
凝固点 3412℃ -38.87℃ -30℃ 0℃

A、钨 B、水银 C、煤油 D、水

查看试题解析
2. 数学中处处存在着美，从三国时期的赵爽弦图，到19世纪的莱洛三角形，再到近代的科克曲线和谢尔宾斯基三角形，这种特殊的数学之美，令人沉述.下列图形中，既是中心对称图形，又是轴对称图形的是（）

A、赵爽弦图 B、莱洛三角形 C、科克曲线 D、谢尔宾斯基三角形

查看试题解析
3. 如图是一款折叠 $L E D$ 护眼灯示意图， $A B$ 是底座， $C D$ 、 $D E$ 分别是长臂和短臂，点C在 $A B$ 上，若 $D E / / A B$ ， $∠ D C A = 70 °$ ，则长臂和短臂的夹角 $∠ C D E =$ （）

A、 $120 °$ B、 $100 °$ C、 $70 °$ D、 $110 °$

查看试题解析
4. 下列计算正确的是（）

A、 $a^{3} \cdot a^{4} = a^{12}$ B、 ${(a^{3})}^{4} = a^{7}$ C、 $a^{3} + a^{2} = a^{5}$ D、 $a^{4} + a^{4} = 2 a^{4}$

查看试题解析
5. 若使用如图所示的a ， b两根直铁丝做成一个三角形框架，需要将其中一根铁丝折成两段，则可以分为两段的铁丝是（）

A、只有a可以 B、只有b可以 C、a ， b都可以 D、a ， b都不可以

查看试题解析
6. 如图是脊柱侧弯的检查示意图，在体检时为方便测出 $C o b b$ 角 $∠ O$ 的大小，需将 $∠ O$ 转化为与它相等的角，则图中与 $∠ O$ 相等的角是（）

A、 $∠ B E A$ B、 $∠ C E A$ C、 $∠ E D B$ D、 $∠ A D O$

查看试题解析
7. 已知关于x的一元二次方程 $x^{2} + 3 x - 2 m = 0$ 的一个根是 $x = 1$ ，则m的值为（）

A、1 B、0 C、 $- 1$ D、2

查看试题解析
8. 在课后服务的乒乓球兴趣课上，老师将从小亮、小莹和小李3人中选2人进行乒乓球对决，恰好选中小莹和小李的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
9. 一个几何体的三视图如图所示，根据图中的相关数据求得该几何体的侧面积为（）

A、 $60 π c m^{2}$ B、 $40 π c m^{2}$ C、 $30 π c m^{2}$ D、 $24 π c m^{2}$

查看试题解析
10. 如图，已知A ， B是反比例函数 $y = \frac{k}{x} (k > 0, x > 0)$ 图象上的两点， $B C / / x$ 轴，交y轴于点C ，动点P从坐标原点O出发，沿 $O \to A \to B \to C$ （图中“→”所示路线）匀速运动，终点为C ，过P作 $P M ⊥ x$ 轴，垂足为M.设三角形 $O M P$ 的面积为S ， P点运动时间为t ，则S关于t的函数图象大致为（）

A、 B、 C、 D、

查看试题解析

二、填空题（本大题6小题，每小题3分，共18分.请将下列各题的正确答案写在答题卡的相应位置.）

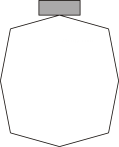
11. 计算 $\frac{a^{2}}{a + 2} - \frac{4}{a + 2}$ 的结果为.

查看试题解析
12. 科学家们测得光在水中的速度约为225000000米/秒，数字225000000用科学记数法表示为．

查看试题解析
13. 如图，在杭州举行的第19届亚运会的奖牌取名“湖山”，以良渚文化中的礼器玉琮为表征，其外轮廓为八边形，这个八边形的内角和是度．

查看试题解析
14. 如图所示的衣架可以近似看成一个等腰三角形 $A B C$ ，其中 $A B = A C$ ， $∠ A B C = 27 °$ ， $B C = 44 c m$ ，则高 $A D$ 约为 $c m$ .（结果精确到 $0.01 c m$ ，参考数据： $s i n 27 ° \approx 0.45$ ， $c o s 27 ° \approx 0.89$ ， $t a n 27 ° \approx 0.51$ ）.

查看试题解析
15. 一商场先用3200元购进一批防紫外线太阳伞，很快就销售一空.商场又用8000元购进了第二批这种太阳伞，所购数量是第一批的2倍，但每把太阳伞贵了4元.则第一次购进这种太阳伞把.

查看试题解析
16. 如图，正方形 $A B C D$ 的边长为4，点E、F分别在边 $B C$ ， $C D$ 上， $A E$ 平分 $∠ B A C$ ，连接 $B F$ ，分别交 $A E$ ， $A C$ 于点G ， H ，且 $A E = B F$ .有下列四个结论：① $A E$ 垂直平分 $B H$ ；②若点P是边 $A B$ 上的一个动点，则 $P H + P C$ 的最小值为 $4 \sqrt{3}$ ；③ $G H^{2} = A G \cdot E G$ ；④ $S_{△ A B H} = 6 \sqrt{2}$ .其中正确的有.

查看试题解析

三、解答题（本大题共9小题，满分72分，解答应写出文字说明、证明过程或演算步骤）

17. 计算： $- 1^{2024} + {(- \frac{1}{2})}^{0} - \sqrt{3} \times \sqrt{6}$

查看试题解析
18. 化简： $(x - y)^{2} - x (x - 2 y)$

查看试题解析
19. 解不等式组 ${\begin{array}{l} x < \frac{5 x + 2}{3} ① \\ 4 x - 2 < 4 + x ② \end{array}$ ，并把解集表示在数轴上.

查看试题解析
20. 如图，在平行四边形 $A B C D$ 中，E是 $A D$ 边上一点.

(1)、实践操作：过点E作 $A B$ 的平行线 $E F$ ，交 $B C$ 于点F（尺规作图，保留作图痕迹，不写作法）.

(2)、推理证明：在（1）的条件下，求证： $△ B A E ≌ △ E F B$ .

查看试题解析
21. 蓬勃发展的快递业，为全国各地的新鲜水果及时走进千家万户提供了极大便利，不同的快递公司在配送、服务、收费和投递范围等方面各具优势.草莓种植户小李经过初步了解，打算从甲、乙两家快递公司中选择一家合作，为此小李收集了10家草莓种植户对两家公司的相关评价，并整理、描述、分析，下面给出了部分信息：
a.配送速度得分（满分10分）：
甲：
6
7
7
8
8
8
8
9
9
10
乙：
7
7
8
8
8
9
9
9
10
10
b.服务质量得分统计图（满分10分）：
c.配送速度和服务质量得分统计表
项目
统计量
快递公司
配送速度得分
服务质量得分
平均数
中位数
平均数
中位数
甲
m
8
7
7
乙
8.5
8.5
7
n
根据以上信息，回答下列问题：

(1)、求出表中m ， n的值；

(2)、在甲乙两家快递公司中，如果某公司服务质量得分的10个数据的波动越小，则认为种植户对该公司的评价越一致.据此推断：甲、乙两家公司中，种植户对的服务质量的评价更一致（填“甲”或“乙”）；

(3)、根据以上数据，小李应该选择哪一家快递公司？请说明理由.（写出一条理由即可）

查看试题解析
22. 某校为了落实“阳光体育活动”，在八年级开展了篮球赛.比赛规则是：八年级10个班级每个班级派出一支队伍参赛，赛制采用的是单循环积分赛（每个班级都与其他9个班级进行一场比赛），胜一场积2分，输一场积1分，然后按照积分高低进行排名.赛程过半，小明所在的班级已经进行了5场比赛，积9分.

(1)、求小明所在班级胜、负的场次各是多少；

(2)、根据分析，总积分超过15分才能确保进入前两名，小明所在班级若想进入前两名在剩下的比赛中至少还要取得几场胜利？

查看试题解析
23. 综合与实践
不借助科学计算器，如何求 $t a n 22.5 °$ 的值？小明进行了如下的实践操作：
如图，已知正方形纸片 $A B C D$ .
第一步：将正方形纸片 $A B C D$ 沿 $A C$ 折叠，展开后得到折痕 $A C$ .
第二步：将 $A B$ 折叠到 $A F$ ，使点B的对应点F恰好落在 $A C$ 上，展开后得到折痕 $A E$ ，点E在线段 $B C$ 上，连接 $E F$ .
问题解决：

(1)、求证： $∠ B A E = 22.5 °$

(2)、请利用小明的实践操作过程，求 $t a n 22.5 °$ 的值.

查看试题解析
24. 如图，在 $▱ A B C D$ 中，连接 $B D$ ，以 $D F$ 为直径的半圆O ，从 $D F$ 与 $A D$ 共线开始绕点D逆时针旋转，直线 $D F$ 与 $D C$ 第一次重合时，停止运动，点K是半圆O的中点，连接 $D K$ ，当 $D F$ ， $D K$ 与线段 $A B$ 有交点时，设交点分别为点P和点Q ，已知 $A B = D F = 8$ ， $∠ B A D = 45 °$ ， $A D = B D$ .

(1)、求 $∠ F D K$ 的度数；

(2)、当点Q在 $A B$ 上时，设 $A Q = x$ ， $B P = y$ ，请求出y与x的关系式；

(3)、当 $D F$ 与 $D B$ 重合时，求半圆O与 $D C$ 所围成的弓形的面积.

查看试题解析
25. 综合与探究：
如图1，抛物线 $y = a x^{2} + b x + \frac{5}{4}$ 与x轴相交于 $A (\frac{1}{2}, 0)$ ， $B (\frac{5}{2}, 0)$ 两点，与y轴交于点C ，连接 $B C$ ，抛物线顶点为点M.

(1)、求抛物线解析式及点M的坐标；

(2)、平移直线 $B C$ 得直线 $y = m x + n$ .
①如图2，若直线 $y = m x + n$ 过点M ，交x轴于点D ，在x轴上取点 $E (\frac{7}{6}, 0)$ ，连接 $E M$ ，求 $∠ D M E$ 的度数.
②把抛物线 $y = a x^{2} + b x + \frac{5}{4}$ 在x轴下方图象沿x轴翻折得到新图象（如图3中的“W”形曲线）.当直线 $y = m x + n$ 与新图象有两个公共点时，请直接写出n的取值范围.

查看试题解析

项目统计量快递公司	配送速度得分		服务质量得分
项目统计量快递公司	平均数	中位数	平均数	中位数
甲	m	8	7	7
乙	8.5	8.5	7	n

物质	钨	水银	煤油	水
凝固点	3412℃	-38.87℃	-30℃	0℃

甲：	6	7	7	8	8	8	8	9	9	10
乙：	7	7	8	8	8	9	9	9	10	10