2024年中考数学考前20天终极冲刺专题之四边形(二)
试卷更新日期:2024-05-21 类型:三轮冲刺
一、选择题
-
1. 如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD,AC于点E,O,连接CE,则CE的长为( )
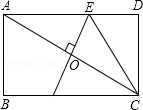 A、3 B、3.5 C、2.5 D、2.82. 在矩形ABCD中,对角线AC、BD相交于点O , AE平分∠BAD交BC于点E , ∠CAE=15°,连接OE , 则下面的结论中正确的有( )
A、3 B、3.5 C、2.5 D、2.82. 在矩形ABCD中,对角线AC、BD相交于点O , AE平分∠BAD交BC于点E , ∠CAE=15°,连接OE , 则下面的结论中正确的有( )①△DOC是等边三角形;②△BOE是等腰三角形;③BC=AB;④∠AOE=135°;⑤S△AOE=S△BOE .
 A、2个 B、3个 C、4个 D、5个3. 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE= ;④AF=2 ,其中正确结论的个数有( )
A、2个 B、3个 C、4个 D、5个3. 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE= ;④AF=2 ,其中正确结论的个数有( )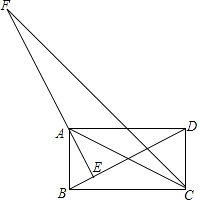 A、1个 B、2个 C、3个 D、4个4. 如图,在正方形中,点在边上,点在边上, , 交于点 , 交于点 , 连接 . 下列结论:①;②;③;④当是的中点时,;⑤当时, . 其中正确结论的序号是
A、1个 B、2个 C、3个 D、4个4. 如图,在正方形中,点在边上,点在边上, , 交于点 , 交于点 , 连接 . 下列结论:①;②;③;④当是的中点时,;⑤当时, . 其中正确结论的序号是 A、①②③④ B、①②③⑤ C、①③④⑤ D、②④⑤5. 如图,在正方形ABCD中,M是边CD上一点,满足 , 连接BM交AC于点N,延长BN到点P使得 , 则( )
A、①②③④ B、①②③⑤ C、①③④⑤ D、②④⑤5. 如图,在正方形ABCD中,M是边CD上一点,满足 , 连接BM交AC于点N,延长BN到点P使得 , 则( ) A、 B、 C、 D、6. 如图,已知是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F, . FG为的角平分线,点H在FG的延长线上, , 连接HA、HC.①;②;③;④;其中说法正确的有( )
A、 B、 C、 D、6. 如图,已知是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F, . FG为的角平分线,点H在FG的延长线上, , 连接HA、HC.①;②;③;④;其中说法正确的有( ) A、1个 B、2个 C、3个 D、4个7. 如图,在 Rt△ABC中,LACB=90°,以其三边为边在AB的同侧作三个正方形,点F在GH 上,CG与EF相交于点P,CM 与BE相交于点Q.若HF=FG则的值是( )
A、1个 B、2个 C、3个 D、4个7. 如图,在 Rt△ABC中,LACB=90°,以其三边为边在AB的同侧作三个正方形,点F在GH 上,CG与EF相交于点P,CM 与BE相交于点Q.若HF=FG则的值是( ) A、 B、 C、 D、8. 如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )
A、 B、 C、 D、8. 如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )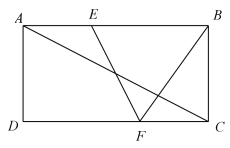 A、 B、 C、4 D、69. 如图,已知在矩形ABCD中,M是AD边的中点,BM与AC垂直,交直线AC于点N,连接DN,则下列四个结论中:①CN=2AN;②DN=DC;③tan∠CAD=;④△AMN∽△CAB.正确的有( )
A、 B、 C、4 D、69. 如图,已知在矩形ABCD中,M是AD边的中点,BM与AC垂直,交直线AC于点N,连接DN,则下列四个结论中:①CN=2AN;②DN=DC;③tan∠CAD=;④△AMN∽△CAB.正确的有( )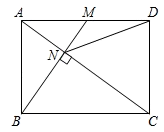 A、①②③④ B、①②③ C、①②④ D、②③④10. 如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,点G是EF的中点,连接CG、BG、BD、DG,下列结论:①BC=DF;②∠ABG+∠ADG=180°;③AC:BG=:1;④若 , 则4S△BDG=25S△DGF . 正确的有( )
A、①②③④ B、①②③ C、①②④ D、②③④10. 如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,点G是EF的中点,连接CG、BG、BD、DG,下列结论:①BC=DF;②∠ABG+∠ADG=180°;③AC:BG=:1;④若 , 则4S△BDG=25S△DGF . 正确的有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB的中点,则△EMN的周长是 .
 12. 如图,在正方形中,点E是边上一点,连接与对角线交于点P , 过点P作交于点F , 连接交于点G ,
12. 如图,在正方形中,点E是边上一点,连接与对角线交于点P , 过点P作交于点F , 连接交于点G ,
下列四个结论:①;②;③;④ . 其中正确结论有 .
13. 如图,正方形 , 点在边上,且 , , 垂足为 , 且交于点与交于点 , 延长至 , 使 , 连接 , 有如下结论:①;②;③;④ .上述结论中,所有正确结论的序号是 .
 14. 如图,在正方形ABCD中, , M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作MN⊥CM,交线段AB于点N.连接NC交BD于点G.若BG:MG=3:5,则NG⋅CG的值为 .
14. 如图,在正方形ABCD中, , M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作MN⊥CM,交线段AB于点N.连接NC交BD于点G.若BG:MG=3:5,则NG⋅CG的值为 . 15. 如图,正方形 中,点 分别在线段 上运动,且满足 , 分别与 BD 相交于点 ,下列说法中:① ;②点 A到线段 EF的距离一定等于正方形的边长;③若 ,则 ;④若 , ,则 .其中结论正确的是;(将正确的序号填写在横线上)
15. 如图,正方形 中,点 分别在线段 上运动,且满足 , 分别与 BD 相交于点 ,下列说法中:① ;②点 A到线段 EF的距离一定等于正方形的边长;③若 ,则 ;④若 , ,则 .其中结论正确的是;(将正确的序号填写在横线上)
三、解答题
-
16. 如图,已知四边形ABCD为正方形,AB= ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
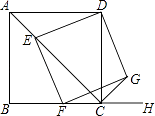
①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
17. (1)、如图1,在直角中, , 过作交于点 , 求证:;(2)、如图2,在菱形中,过作交的延长线于点 , 过作交边于点 . ①若 , 求的值;②若 , 直接写出的值(用含的式子表示);(3)、如图3,在菱形中, , 点在上,且 , 点为上一点,连接 , 过作交于点 , 求的值(用含的式子表示).
(1)、如图1,在直角中, , 过作交于点 , 求证:;(2)、如图2,在菱形中,过作交的延长线于点 , 过作交边于点 . ①若 , 求的值;②若 , 直接写出的值(用含的式子表示);(3)、如图3,在菱形中, , 点在上,且 , 点为上一点,连接 , 过作交于点 , 求的值(用含的式子表示).四、实践探究题
-
18. 如图1,点E为正方形ABCD内一点, , , , 将直角三角形ABE绕点A逆时针方向旋转度()点B、E的对应点分别为点、 .
 (1)、【感知】如图2,在旋转的过程中,点落在了AC上,求此时的长;(2)、【探究】若 , 如图3,得到(此时与D重合),延长BE交于点F , 试判断四边形的形状,并说明理由;(3)、【应用】在直角三角形ABE绕点A逆时针方向旋转过程中,直接写出线段长度的取值范围.19. 综合与实践
(1)、【感知】如图2,在旋转的过程中,点落在了AC上,求此时的长;(2)、【探究】若 , 如图3,得到(此时与D重合),延长BE交于点F , 试判断四边形的形状,并说明理由;(3)、【应用】在直角三角形ABE绕点A逆时针方向旋转过程中,直接写出线段长度的取值范围.19. 综合与实践数学活动课上,同学们用尺规作图法探究在菱形内部作一点到该菱形三个顶点的距离相等.

【动手操作】如题图1,已知菱形ABCD,求作点 , 使得点到三个顶点A,D,C的距离相等.小红同学设计如下步骤:①连接BD
②分别以点A,D为圆心,大于的长为半径分别在AD的上方与下方作弧;AD上方两弧交于点 , 下方两弧交于点 , 作直线MN交BD于点 .
③连接AE,EC,则 .
(1)、根据小红同学设计的尺规作图步骤,在题图1中完成作图过程(要求:用尺规作图并保留作图痕迹).(2)、【证明结论】证明: .(3)、【拓展延伸】当时,求与的面积比.五、综合题
-
20. 如图1,在平行四边形中,为钝角, , 分别为边 , 上的高,交边 , 于点 , , 连结 , .
 (1)、求证:;(2)、求证:;(3)、如图2,若 , 以点为原点建立平面直角坐标系,点坐标为 , 点为直线上一动点,当时,求出此时点的坐标.21. 如图,在矩形中, , 点 , 分别在边、上,且于点.
(1)、求证:;(2)、求证:;(3)、如图2,若 , 以点为原点建立平面直角坐标系,点坐标为 , 点为直线上一动点,当时,求出此时点的坐标.21. 如图,在矩形中, , 点 , 分别在边、上,且于点. (1)、如图1,当时,求证:;(2)、如图2, , 若 , , 求的值;(3)、如图3,在第(2)的条件下,连接交于点 , 连接 , 若 , 求的值.22. 已知在平行四边形ABCD中,动点P在AD边上,以每秒0.5cm的速度从点A向点D运动.
(1)、如图1,当时,求证:;(2)、如图2, , 若 , , 求的值;(3)、如图3,在第(2)的条件下,连接交于点 , 连接 , 若 , 求的值.22. 已知在平行四边形ABCD中,动点P在AD边上,以每秒0.5cm的速度从点A向点D运动. (1)、如图1,在运动过程中,若CP平分∠BCD , 且满足CD=CP , 则∠B=°.(2)、如图2,另一动点Q在BC边上,以每秒2cm的速度从点C出发,在BC间往返运动,P , Q两点同时出发,当点P到达点D时停止运动(同时Q点也停止),若AD=6cm , 当运动时间为秒时,以P , D , Q , B四点组成的四边形是平行四边形.(3)、如图3,连结BP并延长与CD的延长线交于点F , CE平分∠ACF交BF于E点,连接AE , 当AE⊥CE , DF=8时,求AC的长.(4)、如图4,在(1)的条件下,连结BP并延长与CD的延长线交于点F , 连结AF , 若AB=4cm , 求△APF的面积.
(1)、如图1,在运动过程中,若CP平分∠BCD , 且满足CD=CP , 则∠B=°.(2)、如图2,另一动点Q在BC边上,以每秒2cm的速度从点C出发,在BC间往返运动,P , Q两点同时出发,当点P到达点D时停止运动(同时Q点也停止),若AD=6cm , 当运动时间为秒时,以P , D , Q , B四点组成的四边形是平行四边形.(3)、如图3,连结BP并延长与CD的延长线交于点F , CE平分∠ACF交BF于E点,连接AE , 当AE⊥CE , DF=8时,求AC的长.(4)、如图4,在(1)的条件下,连结BP并延长与CD的延长线交于点F , 连结AF , 若AB=4cm , 求△APF的面积.