2024年中考数学考前20天终极冲刺专题之三角形

试卷更新日期：2024-05-21 类型：三轮冲刺

进入出卷网下载

一、选择题

1. 绿色出行，健康出行，你我同行.某市为了方便市民绿色出行，推出了共享单车服务.图1是某品牌共享单车放在水平地面的实物图，图2是其示意图，其中AB、CD都与地面平行，AM与BC平行，若 $∠ B C D = 6 5^{°}$ ，则 $∠ M A B$ 的度数为（）

A、 $6 5^{°}$ B、 $10 0^{°}$ C、 $10 5^{°}$ D、 $11 5^{°}$

查看试题解析
2. 如图，在Rt△ABC中，∠C＝90°，分别以各边为直径作半圆，图中阴影部分在数学史上称为“希波克拉底月牙”，当AC＝4，BC＝2时，则阴影部分的面积为（　　）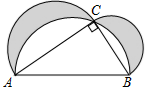

A、4 B、4π C、8π D、8

查看试题解析
3. 如图，一副三角板中两个直角顶点C叠放在一起，其中∠A=30°，∠B=60°，∠D=∠E=45°，保持三角板ABC不动，三角板DCE可绕点C旋转，则下列结论：①∠ACE=∠BCD；②∠BCE+∠ACD随着∠ACD的交化而变化；③当AB∥CE时，则∠ACD=60°或150°；④当∠BCE=3∠ACD时，DE一定垂直于AC．其中正确的个数是（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法中正确的个数是
①AD是∠BAC的平分线；②∠ADC=60°；③点D在AB的中垂线上；④S_△DAC：S_△ABC=1：3.

A、1 B、2 C、3 D、4

查看试题解析
5. 如图，在三角形ABC中，AB=11，AC=15，点M是BC的中点，AD是∠BAC的角平分线，MF∥AD，则FC=（）

A、14 B、13 C、12 D、11

查看试题解析
6. 如图，等边 $△ A B C$ 内有一点E， $B E = 4$ ， $C E = 6$ ，当 $∠ A E B = 150 °$ 时，则 $A E$ 的长为（）

A、2 B、 $2 \sqrt{5}$ C、3 D、 $3 \sqrt{2}$

查看试题解析
7. 如图， $⊙ I$ 是 $R t △ A B C$ 的内切圆， $∠ A C B = 90 °$ ，过点I作 $M N ∥ A B$ 分别交 $C A$ ， $C B$ 于N，M，若 $B M = 3$ ， $A N = 4$ ，则 $⊙ I$ 的半径是（）

A、 $\frac{7}{2}$ B、 $\frac{5}{2}$ C、 $\frac{14}{5}$ D、 $\frac{12}{5}$

查看试题解析
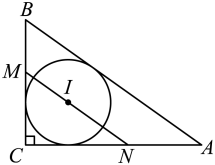8. 如图，点P是在正 $△$ ABC内一点， $P A = 3$ ， $P B = 4$ ， $P C = 5$ ，将线段AP绕点A逆时针旋转60°得到线段 $A P^{'}$ ，连接 $P^{'} P$ ， $P^{'} C$ .下列结论中正确的是（）

① $△ A P^{'} C$ 可以由 $△ A P B$ 绕点A逆时针旋转60°得到；②线段 $P P^{'} = 3$ ；③四边形 $A P C P^{'}$ 的面积为 $6 + 3 \sqrt{3}$ ；④ $S_{△ A P B} + S_{△ B P C} = 6 + 4 \sqrt{3}$ .

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
9. 如图， $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $c o s B = \frac{1}{4}$ ，点D是边BC的中点，以AD为底边在其右侧作等腰三角形ADE，使 $∠ A D E = ∠ B$ ，连接CE，则 $\frac{C E}{A D}$ 的值为（）

A、 $\frac{3}{2}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{15}}{2}$ D、 $2$

查看试题解析
10. 如图，已知Rt△ABC， $A C = B C = 2$ ，将△ABC绕点A沿逆时针方向旋转后得到△ADE，直线BD、CE相交于点F，连接AF，则下列结论中：① $A B = 2 \sqrt{2}$ ；②△ABD∽△ACE；③ $∠ B F C = 45 °$ ；④F为BD的中点，其中正确的有（）

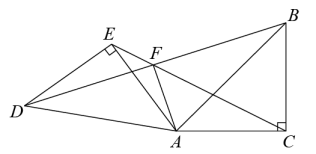A、①②③ B、①②④ C、①②③④ D、②③④

查看试题解析

二、填空题

11. 如图，C为线段AB的中点，D为AB垂直平分线上一点，连接BD ，将BD绕点D顺时针旋转60°得到线段DE ，连接AE ，若AB＝2 $\sqrt{3}$ ， AE＝4，则CD的长为．

查看试题解析
12. 如图，在等边三角形ABC中，点D，E分别是边BC，CA上的点，且BD=CE，连结AD，BE交于点P．连接CP，若CP⊥AP时，则AE：CE= ；设△ABC的面积为S₁ ，四边形CDPE的面积为S₂ ，则 $\frac{S_{2}}{S_{1}}$ ＝．

查看试题解析
13. 如图，在四边形ABCD中，AB＝BC＝6，∠ABC＝60°，∠ADC＝90°，对角线AC与BD相交于点E，若BE＝3DE，则BD＝．

查看试题解析
14. 如图，在△ABC中，∠ACB=90°，AC=3，BC=4，将△ABC绕点A旋转，使点C落在AB边上的点E处，点B落在点D处，连接BD，CE，延长CE交BD于点F，则EF的长为

查看试题解析
15. 矩形ABCD与CEFG如图放置，点B，C，E共线，点C，D，G共线，连接AF，取AF的中点H，连接GH.若BC＝EF＝2，CD＝CE＝1，则GH＝.

查看试题解析

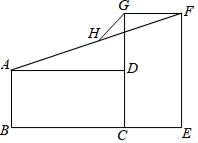
三、解答题

16. 如图，在 $△ A B C$ 中， $A C = 24 c m$ ， $B C = 7 c m$ ，点 $P$ 在 $B C$ 上，从点 $B$ 向点 $C$ 运动 $($ 不包括点 $C)$ ，速度为 $2 c m / s$ ；点 $Q$ 在 $A C$ 上，从点 $C$ 向点 $A$ 运动 $($ 不包括点 $A)$ ，速度为 $5 c m / s .$ 若点 $P$ ， $Q$ 分别从点 $B$ ， $C$ 同时运动，且运动时间记为 $t s$ ，请解答下面的问题，并写出探索的主要过程．

(1)、当 $t$ 为何值时， $P$ ， $Q$ 两点的距离为 $5 \sqrt{2} c m$ ？

(2)、当 $t$ 为何值时， $△ P C Q$ 的面积为 $15 c m^{2}$ ？

(3)、点 $P$ 运动多少时间时，四边形 $B P Q A$ 的面积最小？最小面积是多少？

查看试题解析
17. 已知 $△ A B C$ 和 $△ A D E$ 都是等腰三角形，且 $A B = A C$ ， $A D = A E$ ，若点D在 $B C$ 边上运动时，总保持 $∠ A D E = ∠ B$ ，连接 $C E, D E$ 与 $A C$ 交于点F ．

(1)、①如图1，当点D为 $B C$ 边中点时，则 $\frac{C E}{B C}$ 的值为 ▲ ；
②如图2，当点D不为 $B C$ 边中点时，求证： $C E = B D$ ；

(2)、如图3，当点D在 $B C$ 边上运动中恰好使得 $A E ∥ B C$ 时，若 $A B = 5$ ， $B C = 6$ ，求 $D F$ 的长．

查看试题解析
18. 如图1，在直线MN上摆放一副直角三角板，两三角板顶点重合于点O ， ∠AOB＝60°，∠OCD＝45°，将三角板COD绕点O以每秒6°的速度顺时针方向转动，设转动时间为t秒．

(1)、如图2，若OC平分∠MOB ，则t的最小值为；此时∠DOB﹣∠MOC＝度；（直接写答案）

(2)、当三角板COD转动如图3的位置，此时OC、OD同时在直线OB的右侧，猜想∠DOB与∠MOC有怎样的数量关系？并说明理由；（数量关系中不含t）

(3)、若当三角板COD开始转动的同时，另一个三角板OAB也绕点O以每秒3°的速度顺时针转动，当OC旋转至射线ON上时，两三角板同时停止运动：
①当t为何值时，∠BOC＝15°；
②在转动过程中，请写出∠DOB与∠MOC的数量关系，并说明理由．（数量关系中不含t）

查看试题解析
19. 如图， $C D$ 为 $△ A B C$ 的中线，以 $C D$ 为直角边在其右侧作直角 $△ C D E$ ， $C D 丄 D E$ ， $B C$ 与 $D E$ 交于点F ， $∠ C E D = 30 °$ ．

(1)、如图1，若 $C F = E F = 5$ ，求 $C D$ 的长；

(2)、如图2，若将 $B C$ 绕点C逆时针旋转 $120 °$ 得到 $C G$ ，连接 $A G$ 、 $A E$ ，探究 $A G$ 、 $A E$ 的数量关系，并说明理由；

(3)、如图3，若 $∠ A C B = 90 °$ ， $A C = 2$ ， $B C = 2 \sqrt{3}$ ，直线 $C E$ 上有一点M ，连接 $M F$ ，将 $△ C F M$ 沿着 $M F$ 翻折到 $△ A B C$ 所在的平面内得到 $△ N F M$ ，取 $N F$ 的中点P ，连接 $A P$ ，当 $A P$ 最小时，请直接写出 $△ A P B$ 的面积．

查看试题解析
20. 如图， $△ A B C$ 是等边三角形，D为 $A B$ 上一点，连接 $C D$ ，将 $C D$ 绕点C顺时针旋转120°至 $C E$ ，连接 $B E$ ，分别交 $A C$ 、 $C D$ 于点F、G.

(1)、若 $A D = 3$ ， $B D = 1$ ，求 $△ B C E$ 的面积；

(2)、请猜想线段 $A F$ ， $B D$ ， $C F$ 之间的数量关系，并证明你的猜想；

(3)、当 $△ B C E$ 周长最小时，请直接写出 $\frac{S_{△ C E F}}{S_{四边形 A D G F}}$ 的值.

查看试题解析

四、实践探究题

21. 【教材呈现】如图是华师版七年级下册数学教材第122页的部分内容．
2．如图， $△ A C D$ 、 $△ A E B$ 都是等腰直角三角形， $∠ C A D = ∠ E A B = 90 °$ ，画出 $△ A C E$ 以点 $A$ 为旋转中心、逆时针旋转 $90 °$ 后的三角形．
数学课上，同学们连结 $B D$ 便解决了此问题，随后数学老师追问： $B D$ 与 $E C$ 具有怎样的数量关系？两组同学给出两种不同方法：
甲组：由于 $△ A B D$ 是由 $△ A C E$ 绕着点 $A$ 逆时针旋转 $90 °$ 后得到的，所以 $B D$ 与 $E C$ 为对应线段，所以 $B D = E C$ ．
乙组：根据题意，我们可以证明 $△ A B D ≌ △ A C E$ ，因此 $B D = E C$ ．

(1)、请结合图①写出乙组证明方法的完整过程．

(2)、【类比探究】若将【教材呈现】中的等腰直角三角形换成等边三角形，上述结论是否仍然成立？
如图②， $△ A C D$ 、 $△ A E B$ 都是等边三角形，连结 $E C$ 、 $B D$ 、 $E D$ ．
①则 $B D$ 与 $E C$ 的数量关系是．
②若 $∠ D E A = 30 °, A B = 8, E D = 12$ ，则 $E C$ 长为．

(3)、【拓展应用】 $△ A C D$ 、 $△ A E B$ 都是等边三角形， $A C = 4, A B = 8$ ，若将 $△ A C D$ 绕着点 $A$ 旋转一周，在运动过程中，点 $B$ 到直线 $E D$ 的距离设为 $d$ ，则 $d$ 的取值范围是．

查看试题解析
22.

(1)、【问题初探】数学课上，李老师出示了这样一个问题：如图1，在 $△ A B C$ 中， $A B = A C$ ，点F是 $A C$ 上一点，点E是 $A B$ 延长线上的一点，连接 $E F$ ，交 $B C$ 于点D ，若 $E D = D F$ ，求证： $B E = C F$ ．
①如图2，小乐同学从中点的角度，给出了如下解题思路：在线段 $D C$ 上截取 $D M$ ，使 $D M = B D$ ，连接 $F M$ ，利用两个三角形全等和已知条件，得出结论；
②如图3，小亮同学从平行线的角度给出了另一种解题思路：过点E作 $E M ∥ A C$ 交 $C B$ 的延长线于点M ，利用两个三角形全等和已知条件，得出了结论；
请你选择一位同学的解题思路，写出证明过程；

(2)、【类比分析】李老师发现两位同学的做法非常巧妙，为了让同学们更好的理解这种转化的思想方法，李老师提出了新的问题，请你解答，
如图4，在 $△ A B C$ 中，点E在线段 $A B$ 上，D是 $B C$ 的中点，连接 $C E$ ， $A D$ ， $C E$ 与 $A D$ 相交于点N ，若 $∠ E A D + ∠ A N C = 180 °$ ，求证： $A B = C N$ ；

(3)、【学以致用】如图5，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $∠ C = 30 °$ ， $A F$ 平分 $∠ B A C$ ，点E在线段 $B A$ 的延长线上运动，过点E作 $E D ∥ A F$ ，交 $A C$ 于点N ，交 $B C$ 于点D ，且 $B D = C D$ ，请直接写出线段 $A E$ ， $C N$ 和 $B C$ 之间的数量关系．

查看试题解析