2024中考数学考前20天终极冲刺专题之二次函数
试卷更新日期:2024-05-21 类型:三轮冲刺
一、选择题
-
1. 经过两点的抛物线(为自变量)与轴有交点,则线段长为( )A、10 B、12 C、13 D、152. 如图是小颖家门口的路灯示意图,为垂直于地面的竖直灯杆(点在地面上),灯杆顶端与灯泡之间用一根曲杆连接,曲杆的形状可看成是一条抛物线的一部分,以为坐标原点,所在直线为轴,建立如图所示的平面直角坐标系,已知该拋物线的顶点 , 竖直灯杆的高度为 , 灯泡到轴的水平距离为 , 则灯泡到地面的高度为( )
 A、 B、 C、 D、3. 如图,抛物线经过点 , 且 , 有下列结论:①;②;③;④若点在抛物线上,则 . 其中,正确的结论有( )
A、 B、 C、 D、3. 如图,抛物线经过点 , 且 , 有下列结论:①;②;③;④若点在抛物线上,则 . 其中,正确的结论有( ) A、4个 B、3个 C、2个 D、1个4. 已知ac≠0,若二次函数y1=ax2+bx+c的图象与x轴交于两个不同的点A(x1 , 0),B(x2 , 0),二次函数y2=cx2+bx+a的图象与x轴交于两个不同的点C(x3 , 0),D(x4 , 0),则( )A、x1+x2+x3+x4=1 B、x1x2x3x4=1 C、 D、5. 如图,抛物线经过点 , . 下列结论:①;②;③若抛物线上有点 , , , 则;④方程的解为 , , 其中正确的个数是( )
A、4个 B、3个 C、2个 D、1个4. 已知ac≠0,若二次函数y1=ax2+bx+c的图象与x轴交于两个不同的点A(x1 , 0),B(x2 , 0),二次函数y2=cx2+bx+a的图象与x轴交于两个不同的点C(x3 , 0),D(x4 , 0),则( )A、x1+x2+x3+x4=1 B、x1x2x3x4=1 C、 D、5. 如图,抛物线经过点 , . 下列结论:①;②;③若抛物线上有点 , , , 则;④方程的解为 , , 其中正确的个数是( )
 A、4 B、3 C、2 D、16. 在平面直角坐标系xOy中,O为坐标原点,抛物线 的对称轴为 与x轴的一个交点位于 , 两点之间.下列结论:其中正确的是( )A、 B、 C、 D、若、为方程 的两个根,则7. 函数的图象是由函数的图象x轴上方部分不变,下方部分沿x轴向上翻折而成,如图所示,则下列结论正确的是( )
A、4 B、3 C、2 D、16. 在平面直角坐标系xOy中,O为坐标原点,抛物线 的对称轴为 与x轴的一个交点位于 , 两点之间.下列结论:其中正确的是( )A、 B、 C、 D、若、为方程 的两个根,则7. 函数的图象是由函数的图象x轴上方部分不变,下方部分沿x轴向上翻折而成,如图所示,则下列结论正确的是( )①;②;③;④图象向上平移2个单位后与直线有3个交点.
 A、①② B、①③④ C、②③④ D、①③8. 已知 关于 的二次函数 , 下列结论中, 正确的序号是( )
A、①② B、①③④ C、②③④ D、①③8. 已知 关于 的二次函数 , 下列结论中, 正确的序号是( )① 当 时, 函数图象的顶点坐标为 ;②当 时,函数图象总过定点;③当 时, 函数图象在 轴上截得的线段的长度大于 ;④若函数图象上任取不同的两点 , , 则当 , 函数在 时,一定能使 成立.
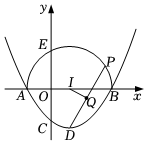
A、①② B、①③④ C、①②③ D、①②③④9. 如图,抛物线与轴交于点 , , 与轴交于点 , 顶点为 , 以为直径在轴上方画半圆交轴于点 , 圆心为 , 是半圆上一动点,连接 , 点为的中点.下列四种说法:点在上;
;
当点沿半圆从点运动至点时,点运动的路径长为;
线段的长可以是 .
其中正确说法的个数为( )
 A、个 B、个 C、个 D、个10. 如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a<0)交x轴于A,B两点(B在A左侧),交y轴于点C,且CO=AO,分别以BC,AC为边向外作正方形BCDE、正方形ACGH,记它们的面积分别为S1 , S2 , △ABC面积记为S3 , 当S1+S2=6S3时,b的值为( )
A、个 B、个 C、个 D、个10. 如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a<0)交x轴于A,B两点(B在A左侧),交y轴于点C,且CO=AO,分别以BC,AC为边向外作正方形BCDE、正方形ACGH,记它们的面积分别为S1 , S2 , △ABC面积记为S3 , 当S1+S2=6S3时,b的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若关于x的方程恰有三个根,则t的值为.12. 在抛物线上,过轴上点作两条相互垂直的直线与抛物线分别交于 , , , , 且 , 分别是线段 , 的中点,面积的最小值为 .13. 如图,在平面直角坐标系中,点 在抛物线 上,过点A作y轴的垂线,交抛物线于另一点B,点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为.
 14. 如图,二次函数 , 其对称轴为直线 , 且与x轴交于点、 , 其中 , 下列结论:
14. 如图,二次函数 , 其对称轴为直线 , 且与x轴交于点、 , 其中 , 下列结论:①;②;③;④;⑤
其中正确的有 . (填写正确的序号)

三、解答题
-
15. 已知甲、乙两种玩具每件的进价分别为10元和15元.经市场调查发现,甲种玩具每天的销量(单位:件)与每件售价x(单位:元)的函数关系为 , 乙种玩具每天的销量(单位:件)与每件售价z(单位:元)之间是一次函数关系,其部分数据如下表:
每件售价z(单位:元)
…
20
25
30
…
销量(单位:件)
…
100
80
60
…
其中x , z均为非负整数.商店按照每件甲种玩具利润是每件乙种玩具利润的2倍来确定甲、乙两种玩具的销售单价,且销售单价高于进价.
(1)、直接写出乙种玩具每天的销量与每件售价z的关系式是;甲种玩具每件售价x与乙种玩具每件售价z的关系式是;(2)、当甲种玩具的总利润为800元时,求乙种玩具的总利润是多少元?(3)、当这两种玩具每天销售的总利润之和最大时,直接写出甲种玩具每件的销售价格.16. 图①是古代的一种远程投石机,其投出去的石块运动轨迹是抛物线的一部分.据《范蠡兵法》记载:“飞石重十二斤,为机发,行二百步”,其原理蕴含了物理中的“杠杆原理”.在如图②所示的平面直角坐标系中,将投石机置于斜坡的底部点O处,石块从投石机竖直方向上的点C处被投出,已知石块运动轨迹所在抛物线的顶点坐标是 , . (1)、求抛物线的表达式;(2)、在斜坡上的点A建有垂直于水平线的城墙 , 且 , , , 点D , A , B在一条直线上.通过计算说明石块能否飞越城墙 .17. 排球考试要求:垫球后,球在运动中离地面的最大高度至少为2米.某次模拟测试中,某生在处将球垫偏,之后又在A、两处先后垫球,球沿抛物线运动(假设抛物线、、在同一平面内),最终正好在处垫住,处离地面的距离为1米.如图所示,以为坐标原点1米为单位长度建立直角坐标系,轴平行于地面水平直线 , 已知点 , 点的横坐标为 , 抛物线表达式为和抛物线表达式为 .
(1)、求抛物线的表达式;(2)、在斜坡上的点A建有垂直于水平线的城墙 , 且 , , , 点D , A , B在一条直线上.通过计算说明石块能否飞越城墙 .17. 排球考试要求:垫球后,球在运动中离地面的最大高度至少为2米.某次模拟测试中,某生在处将球垫偏,之后又在A、两处先后垫球,球沿抛物线运动(假设抛物线、、在同一平面内),最终正好在处垫住,处离地面的距离为1米.如图所示,以为坐标原点1米为单位长度建立直角坐标系,轴平行于地面水平直线 , 已知点 , 点的横坐标为 , 抛物线表达式为和抛物线表达式为 . (1)、求抛物线的函数表达式;(2)、第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由;(3)、为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该生第三次垫球处离地面的高度至少为多少米?18. 如图,在平面直角坐标系中,抛物线 , 若抛物线与x轴交于 , 两点,与轴交于点 .
(1)、求抛物线的函数表达式;(2)、第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由;(3)、为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该生第三次垫球处离地面的高度至少为多少米?18. 如图,在平面直角坐标系中,抛物线 , 若抛物线与x轴交于 , 两点,与轴交于点 . (1)、求该抛物线的函数表达式;(2)、如图1,若点是直线下方的抛物线上一点,过点作 , 交轴于点 , 且 , 求点的横坐标;(3)、如图2,点在点的正下方,连接 , 交抛物线于点 , 直线交对称轴于点 , 作 , 交射线于点 , 求的大小.
(1)、求该抛物线的函数表达式;(2)、如图1,若点是直线下方的抛物线上一点,过点作 , 交轴于点 , 且 , 求点的横坐标;(3)、如图2,点在点的正下方,连接 , 交抛物线于点 , 直线交对称轴于点 , 作 , 交射线于点 , 求的大小.四、实践探究题
-
19. 综合与应用
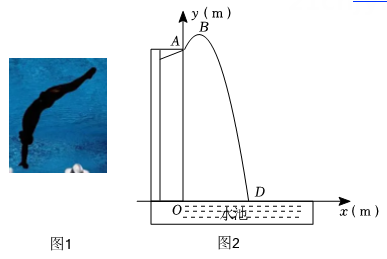
如果将运动员的身体看作一点,则他在跳水过程中运动的轨迹可以看作为抛物线的一部分.建立如图2所示的平面直角坐标系xOy,运动员从点A(0,10)起跳,从起跳到入水的过程中,运动员的竖直高度y (m)与水平距离x (m)满足二次函数的关系.
 (1)、在平时的训练完成一次跳水动作时,运动员甲的水平距离x与竖直高度y的几组数据如下表:
(1)、在平时的训练完成一次跳水动作时,运动员甲的水平距离x与竖直高度y的几组数据如下表:水平距离x(m)
0 1
1.5
竖直高度y(m)
10
10
6.25
根据上述数据,求出y关于x的关系式;
(2)、在(1)的这次训练中,求运动员甲从起点A到入水点的水平距离OD的长;(3)、信息1:记运动员甲起跳后达到最高点B到水面的高度为k(m),从到达到最高点B开始计时,则他到水面的距离h (m)与时间t (s)之间满足h=-5t2+k .信息2:已知运动员甲在达到最高点后需要1.6s的时间才能完成极具难度的270C 动作.
问题解决:
①请通过计算说明,在(1)的这次训练中,运动员甲能否成功完成此动作?
②运动员甲进行第二次跳水训练,此时他的竖直高度y(m)与水平距离x (m)的关系为y =ax2-ax+10(a<0),若选手在达到最高点后要顺利完成270C 动作,则a的取值范围是 ▲ .
五、综合题
-
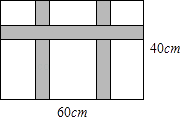
20. 在“文博会”期间,某公司展销如图所示的长方形工艺品,该工艺品长60cm,宽40cm,中间镶有宽度相同的三条丝绸花边.
 (1)、若丝绸花边的面积为650cm2 , 求丝绸花边的宽度;(2)、已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天所需支付的各种费用2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,同时,为了完成销售任务,该公司每天至少要销售800件,那么该公司应该把销售单价定为多少元,才能使每天所获销售利润最大?最大利润是多少?21. 如图,抛物线 经过坐标原点O与点 ,正比例函数 与抛物线交于点 .
(1)、若丝绸花边的面积为650cm2 , 求丝绸花边的宽度;(2)、已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天所需支付的各种费用2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,同时,为了完成销售任务,该公司每天至少要销售800件,那么该公司应该把销售单价定为多少元,才能使每天所获销售利润最大?最大利润是多少?21. 如图,抛物线 经过坐标原点O与点 ,正比例函数 与抛物线交于点 .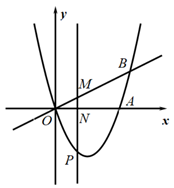 (1)、求该抛物线的函数表达式;(2)、点P是第四象限抛物线上的一个动点,过点P作 轴于点N,交 于点M,是否存在点P,使得 与以点N、A、P为顶点的三角形相似?若存在,请求出点P的坐标;若不存在,请说明理由.22. 根据以下素材,探索完成任务.
(1)、求该抛物线的函数表达式;(2)、点P是第四象限抛物线上的一个动点,过点P作 轴于点N,交 于点M,是否存在点P,使得 与以点N、A、P为顶点的三角形相似?若存在,请求出点P的坐标;若不存在,请说明理由.22. 根据以下素材,探索完成任务.如何设计跳长绳方案
素材1
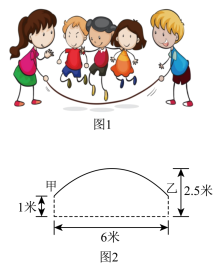
图1是集体跳长绳比赛,比赛时,各队跳绳10人,摇绳2人,共计12人.图2是绳甩到最高处时的示意图,可以近似的看作一条抛物线,正在甩绳的甲、乙两位队员拿绳的手间距6米,到地面的距离均为1米,绳子最高点距离地面2.5米.
素材2
某队跳绳成员有6名男生和4名女生,男生身高1.70米至1.80米,女生身高1.66米至1.68米.跳长绳比赛时,可以采用一路纵队或两路纵队并排的方式安排队员位置,但为了保证安全,人与人之间距离至少0.5米.
问题解决
任务1
确定长绳形状
在图2中建立合适的直角坐标系,并求出抛物线的函数表达式.
任务2
探究站队方式
当该队以一路纵队的方式跳绳时,绳子能否顺利的甩过所有队员的头顶?
任务3
拟定位置方案
为了更顺利的完成跳绳,现按中间高两边低的方式居中安排站位.请在你所建立的坐标系中,求出左边第一位跳绳队员横坐标的最大取值范围.
-