(通用版)2024年中考数学重点知识冲刺训练---图形的变化
试卷更新日期:2024-05-20 类型:三轮冲刺
一、选择题
-
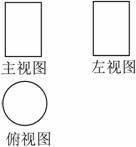
1. 已知某几何体的三视图如图所示,则该几何体可能是( )
 A、
A、 B、
B、 C、
C、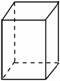 D、
D、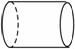 2. 的值为( )A、 B、 C、1 D、3. 在 Rt 中, 所对的边分别是 , 则下列各式中, 正确的是( )A、 B、 C、 D、4. 下列选项中的垃圾分类图标,既是中心对称图形,又是轴对称图形的是( )
2. 的值为( )A、 B、 C、1 D、3. 在 Rt 中, 所对的边分别是 , 则下列各式中, 正确的是( )A、 B、 C、 D、4. 下列选项中的垃圾分类图标,既是中心对称图形,又是轴对称图形的是( )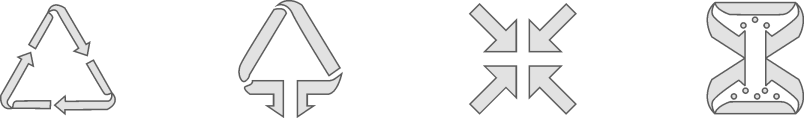 A、可回收物 B、其他垃圾 C、有害垃圾 D、厨余垃圾5. 若 , 则( )A、6 B、 C、1 D、6. 如图,已知 , , 若的长度为6,则的长度为( )
A、可回收物 B、其他垃圾 C、有害垃圾 D、厨余垃圾5. 若 , 则( )A、6 B、 C、1 D、6. 如图,已知 , , 若的长度为6,则的长度为( )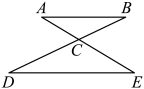 A、4 B、9 C、12 D、7. 如图,是半圆的直径,点在半圆上, , 连接 , 过点作 , 交的延长线于点 . 设的面积为的面积为 , 若 , 则的值为( )
A、4 B、9 C、12 D、7. 如图,是半圆的直径,点在半圆上, , 连接 , 过点作 , 交的延长线于点 . 设的面积为的面积为 , 若 , 则的值为( )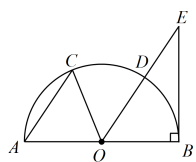 A、 B、 C、 D、8. 在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,可以增加视觉美感.如图,按此比例设计一座高度为2m 的雷锋雕像,那么该雕像的下部设计高度约是( )(结果精确到 .参考数据: , , )
A、 B、 C、 D、8. 在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,可以增加视觉美感.如图,按此比例设计一座高度为2m 的雷锋雕像,那么该雕像的下部设计高度约是( )(结果精确到 .参考数据: , , ) A、 B、 C、 D、9. 如图,在中,点D在边上,过点D作 , 交于点E.若 , 则的值是( )
A、 B、 C、 D、9. 如图,在中,点D在边上,过点D作 , 交于点E.若 , 则的值是( ) A、 B、 C、 D、10. 如图,在平面直角坐标系中,矩形ABCD的顶点A , C分别在x轴,y轴的正半轴上,点D(-2,3),AD=5,若反比例函数 (k>0,x>0)的图象经过点B , 则k的值为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,矩形ABCD的顶点A , C分别在x轴,y轴的正半轴上,点D(-2,3),AD=5,若反比例函数 (k>0,x>0)的图象经过点B , 则k的值为( )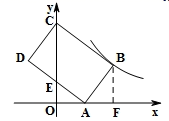 A、 B、8 C、10 D、
A、 B、8 C、10 D、二、填空题
-
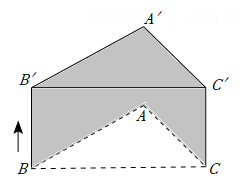
11. 如图,△ABC的边BC长为4 cm.将△ABC平移2 cm得到△A'B'C',且 BB'⊥BC,则阴影部分的面积为cm2.
 12. 如图,在Rt中, , 若 , 则.
12. 如图,在Rt中, , 若 , 则.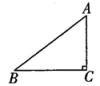 13. 在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法,所做将矩形窗框分为上下两部分,其中E为边的黄金分割点,即.已知为2米,则线段的长为米.
13. 在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法,所做将矩形窗框分为上下两部分,其中E为边的黄金分割点,即.已知为2米,则线段的长为米.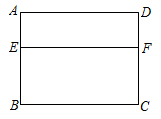 14. 如图,在平面直角坐标系中,C,A 分别为x轴、y轴正半轴上的点,以 OA,OC为边,在第一象限内作矩形OABC,且将矩形 OABC翻折,使点 B与原点O 重合,折痕为 MN,点C 的对应点 C'落在第四象限,过 M点的反比例函数的图象恰好过MN的中点,则点 C'的坐标为.
14. 如图,在平面直角坐标系中,C,A 分别为x轴、y轴正半轴上的点,以 OA,OC为边,在第一象限内作矩形OABC,且将矩形 OABC翻折,使点 B与原点O 重合,折痕为 MN,点C 的对应点 C'落在第四象限,过 M点的反比例函数的图象恰好过MN的中点,则点 C'的坐标为.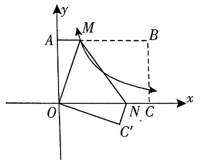
三、解答题
-
15. 计算:2cos60°+(−1)2017+|−3|−(2−1)0.16. 在 的方格中,△ABC的三个顶点都在格点上.
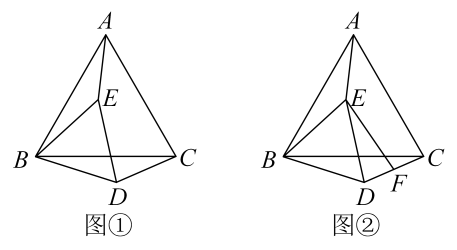
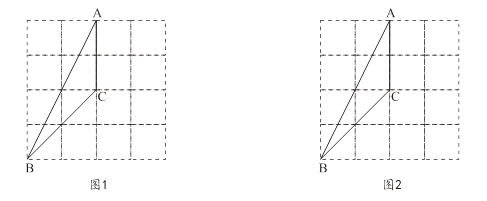 (1)、在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可);(2)、将图2中的△ABC绕着点C按顺时针方向旋转90°,画出经旋转后的三角形.17. 图1是一款笔记本电脑支架,它便于电脑散热,减轻使用者的颈椎压力.图2是支架与电脑底部的接触面以及侧面的抽象图.已知AC,BD互相平分于点O,AC=BD=24cm,若∠AOB=60°,∠DCE=37°.
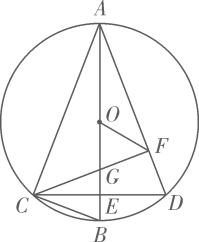
(1)、在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可);(2)、将图2中的△ABC绕着点C按顺时针方向旋转90°,画出经旋转后的三角形.17. 图1是一款笔记本电脑支架,它便于电脑散热,减轻使用者的颈椎压力.图2是支架与电脑底部的接触面以及侧面的抽象图.已知AC,BD互相平分于点O,AC=BD=24cm,若∠AOB=60°,∠DCE=37°. (1)、求CD的长.(2)、求点D到底架CE的高DF(结果精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).18. 如图, 在 中, 弦 的长为 8 , 点 在 的延长线上, 且 .
(1)、求CD的长.(2)、求点D到底架CE的高DF(结果精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).18. 如图, 在 中, 弦 的长为 8 , 点 在 的延长线上, 且 . (1)、求 的半径.(2)、求 的正切值.19. 在中, , 于点于点 , AE,CD相交于点.
(1)、求 的半径.(2)、求 的正切值.19. 在中, , 于点于点 , AE,CD相交于点. (1)、求证:.(2)、若 , 求的面积.20. 如图,在中, , 以为直径作交于点D , 过点O作的平行线 , 交于点E , 作射线交的延长线于点F , 连接 .
(1)、求证:.(2)、若 , 求的面积.20. 如图,在中, , 以为直径作交于点D , 过点O作的平行线 , 交于点E , 作射线交的延长线于点F , 连接 .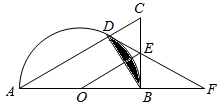 (1)、求证:是的切线;(2)、若 , , 求图中阴影部分的面积.
(1)、求证:是的切线;(2)、若 , , 求图中阴影部分的面积.四、综合题
-
21. 在△ABC中,∠C=90°.(1)、已知c=8 , ∠A=60°,求∠B,a,b;(2)、已知a=3 , ∠A=45°,求∠B,b,c.