(通用版)2024年中考数学重点知识冲刺训练---图形的性质
试卷更新日期:2024-05-20 类型:三轮冲刺
一、选择题
-
1. 如图,在正方形网格内,线段的两个端点都在格点上,网格内另有四个格点,下面四个结论中,正确的是( )
 A、连接 , 则 B、连接 , 则 C、连接 , 则 D、连接 , 则2. 下列长度的各组线段能组成一个三角形的是( )A、 B、 C、 D、3. 如图,工人砌墙时,先在两个墙脚的位置分别插一根木桩,再拉一条直的参照线,就能使砌的砖在一条直线上.这样做应用的数学知识是( )
A、连接 , 则 B、连接 , 则 C、连接 , 则 D、连接 , 则2. 下列长度的各组线段能组成一个三角形的是( )A、 B、 C、 D、3. 如图,工人砌墙时,先在两个墙脚的位置分别插一根木桩,再拉一条直的参照线,就能使砌的砖在一条直线上.这样做应用的数学知识是( ) A、两点之间,线段最短 B、两点确定一条直线 C、垂线段最短 D、三角形两边之和大于第三边4. 如图,在线段 、 、 、 中,长度最小的是( )
A、两点之间,线段最短 B、两点确定一条直线 C、垂线段最短 D、三角形两边之和大于第三边4. 如图,在线段 、 、 、 中,长度最小的是( ) A、线段 B、线段 C、线段 D、线段5. 下列命题中,是真命题的有( )
A、线段 B、线段 C、线段 D、线段5. 下列命题中,是真命题的有( )①对角线相等且互相平分的四边形是矩形②对角线互相垂直的四边形是菱形③四边相等的四边形是正方形④四边相等的四边形是菱形
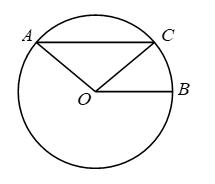
A、①② B、①④ C、②③ D、③④6. 如图,AB、BC为的两条弦,连接OA、OC,点D为AB的延长线上一点,若 , 则的度数为( ) A、100° B、118° C、124° D、130°7. 如图,直线AB,CD相交于点.若 , 则的度数为( )
A、100° B、118° C、124° D、130°7. 如图,直线AB,CD相交于点.若 , 则的度数为( ) A、 B、 C、 D、8. 如图,直线l1l2 , 点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( )
A、 B、 C、 D、8. 如图,直线l1l2 , 点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( ) A、10° B、15° C、20° D、30°9. 我国古代数学的许多创新与发明都曾在世界上有重要影响.下列图形“杨辉三角”“中国七巧板”“刘微割圆术”“赵爽弦图”中,中心对称图形是( ).A、
A、10° B、15° C、20° D、30°9. 我国古代数学的许多创新与发明都曾在世界上有重要影响.下列图形“杨辉三角”“中国七巧板”“刘微割圆术”“赵爽弦图”中,中心对称图形是( ).A、 B、
B、 C、
C、 D、
D、 10. 若某三角形的三边长分别为3,4,m,则m的值可以是( )A、1 B、5 C、7 D、9
10. 若某三角形的三边长分别为3,4,m,则m的值可以是( )A、1 B、5 C、7 D、9二、填空题
-
11. 如图,在中,弦半径 , 则的度数为 .
 12. 如图,点分别在的边上,且 , 点在线段的延长线上.若 , , 则 .
12. 如图,点分别在的边上,且 , 点在线段的延长线上.若 , , 则 .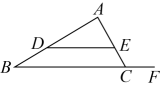 13. 如图所示的五边形花环是用五个全等的等腰三角形拼成的,则∠BAC的度数为.
13. 如图所示的五边形花环是用五个全等的等腰三角形拼成的,则∠BAC的度数为. 14. 如图,在菱形ABCD中,若AC=6,BD=8,则菱形ABCD的面积是 .
14. 如图,在菱形ABCD中,若AC=6,BD=8,则菱形ABCD的面积是 .
三、解答题
-
15. 如图,在菱形ABCD中, , 点在BA的延长线上,对角线AC与BD交于点M,EM交AD于点 , 且.
 (1)、求的度数;(2)、求证:.16. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且BE=CF,求证:△ABE≌△BCF.
(1)、求的度数;(2)、求证:.16. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且BE=CF,求证:△ABE≌△BCF.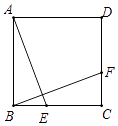 17. 如图,是的直径,点C , D是上异侧的两点, , 交的延长线于点E , 且平分 .
17. 如图,是的直径,点C , D是上异侧的两点, , 交的延长线于点E , 且平分 . (1)、求证:是的切线.(2)、若 , , 求图中阴影部分的面积.18. 如图①, 在矩形 中, . 对角线 相交于点 , 点 分别在对角线 上, , 连结 .
(1)、求证:是的切线.(2)、若 , , 求图中阴影部分的面积.18. 如图①, 在矩形 中, . 对角线 相交于点 , 点 分别在对角线 上, , 连结 . (1)、求线段 的长和 的度数.(2)、 当点 在点 附近 (即点 在点 的左下方) 时, 以 为边在右下方作等边三角形 , 连结 . 在点 运动的过程中, 点 也随之运动. 如图 35-4②, 过点 作 的平行线, 交 于点 . 设线段 的长为 , 线段 的长为 , 求 关于 的函数表达式, 并写出相应的 的取值范围.(3)、 若点 在直线 上运动, 以 为边作等边三角形 . 当点 恰好落在矩形 的边上时, 求 的长.19. 如图,在一个正六边形中,点是该正六边形的中心,将该六边形的每条边延长,延长线的交点分别为、、、、、 .
(1)、求线段 的长和 的度数.(2)、 当点 在点 附近 (即点 在点 的左下方) 时, 以 为边在右下方作等边三角形 , 连结 . 在点 运动的过程中, 点 也随之运动. 如图 35-4②, 过点 作 的平行线, 交 于点 . 设线段 的长为 , 线段 的长为 , 求 关于 的函数表达式, 并写出相应的 的取值范围.(3)、 若点 在直线 上运动, 以 为边作等边三角形 . 当点 恰好落在矩形 的边上时, 求 的长.19. 如图,在一个正六边形中,点是该正六边形的中心,将该六边形的每条边延长,延长线的交点分别为、、、、、 . (1)、证明四边形是菱形;(2)、若的长为6,请计算正六边形的面积.20. 为了监控危险路段的车辆行驶情况, 通常会设置电子眼进行区间测速. 如图 40-5, 电子眼位于点 处, 离地面的铅垂高度 为 , 离坡 的最短距离是 , 坡 的坡比为 , 电子眼照射在 处时, 电子眼的俯角为 , 电子眼照射在坡角点 处时, 电子眼的俯角为 四点在同一平面内).
(1)、证明四边形是菱形;(2)、若的长为6,请计算正六边形的面积.20. 为了监控危险路段的车辆行驶情况, 通常会设置电子眼进行区间测速. 如图 40-5, 电子眼位于点 处, 离地面的铅垂高度 为 , 离坡 的最短距离是 , 坡 的坡比为 , 电子眼照射在 处时, 电子眼的俯角为 , 电子眼照射在坡角点 处时, 电子眼的俯角为 四点在同一平面内). (1)、求路段 的长 .(2)、 求路段 的长 , 结果保留整数).(3)、 如图 40-5 所示的这辆车看成矩形 , 车高 , 当 过 点时开始测速, 过 点时结束测速, 若在这个测速路段车辆所用的时间是 . 该路段限速 , 计算说明该车是否超速.
(1)、求路段 的长 .(2)、 求路段 的长 , 结果保留整数).(3)、 如图 40-5 所示的这辆车看成矩形 , 车高 , 当 过 点时开始测速, 过 点时结束测速, 若在这个测速路段车辆所用的时间是 . 该路段限速 , 计算说明该车是否超速.四、综合题
-
21. 已知:如图,点A、B、C、D在一条直线上, .
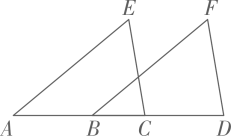 (1)、求证: ;(2)、若 ,求 的度数.22. 如图,在平行四边形中,为线段的中点,连接 , , 延长 , 交于点 , 连接 , .
(1)、求证: ;(2)、若 ,求 的度数.22. 如图,在平行四边形中,为线段的中点,连接 , , 延长 , 交于点 , 连接 , . (1)、求证:四边形是矩形;(2)、若 , , 求四边形的面积.23. 和均为等边三角形,点E、D分别从点A,B同时出发,以相同的速度沿运动,运动到点B、C停止.
(1)、求证:四边形是矩形;(2)、若 , , 求四边形的面积.23. 和均为等边三角形,点E、D分别从点A,B同时出发,以相同的速度沿运动,运动到点B、C停止.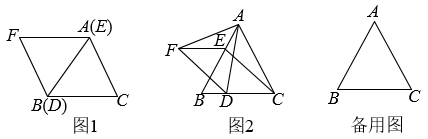 (1)、如图1,当点E、D分别与点A、B重合时,请判断:线段的数量关系是 , 位置关系是;(2)、如图2,当点E、D不与点A,B重合时,(1)中的结论是否依然成立?若成立,请给予证明;若不成立,请说明理由;(3)、当点D运动到什么位置时,四边形的面积是面积的一半,请直接写出答案;此时,四边形是哪种特殊四边形?请在备用图中画出图形并给予证明.
(1)、如图1,当点E、D分别与点A、B重合时,请判断:线段的数量关系是 , 位置关系是;(2)、如图2,当点E、D不与点A,B重合时,(1)中的结论是否依然成立?若成立,请给予证明;若不成立,请说明理由;(3)、当点D运动到什么位置时,四边形的面积是面积的一半,请直接写出答案;此时,四边形是哪种特殊四边形?请在备用图中画出图形并给予证明.