2024年中考数学考前20天终极冲刺专题之反比例函数
试卷更新日期:2024-05-20 类型:三轮冲刺
一、选择题
-
1. 若点都在反比例函数的图象上,则的大小关系是( )A、 B、 C、 D、2. 如图,反比例函数的图象经过矩形对角线的交点 , 分别于交于点 , 若四边形的面积为12,则的值为( )
 A、2 B、3 C、4 D、53. 如图,直线分别交x轴、y轴于A , B , M是反比例函数的图象上位于直线上方的一点,轴交AB于C , 交AB于D , , 则k的值为( )
A、2 B、3 C、4 D、53. 如图,直线分别交x轴、y轴于A , B , M是反比例函数的图象上位于直线上方的一点,轴交AB于C , 交AB于D , , 则k的值为( ) A、8 B、 C、4 D、4. 如图,四个边长均为的正方形如图摆放,其中三个顶点位于坐标轴上,其中一个顶点在反比例函数的图象上,则的值为( )
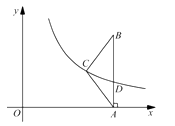
A、8 B、 C、4 D、4. 如图,四个边长均为的正方形如图摆放,其中三个顶点位于坐标轴上,其中一个顶点在反比例函数的图象上,则的值为( ) A、 B、 C、 D、5. 如图,在直角坐标系xOy中,点A,B分别在x轴和y轴, . ∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=的图象过点C.当以CD为边的正方形的面积为时,k的值是( )
A、 B、 C、 D、5. 如图,在直角坐标系xOy中,点A,B分别在x轴和y轴, . ∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=的图象过点C.当以CD为边的正方形的面积为时,k的值是( )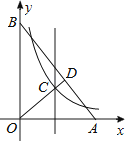 A、2 B、3 C、5 D、76. 如图,在平面直角坐标系中,点、都在反比例函数的图象上,延长交轴于点 , 作轴于点 , 连接、 , 并延长交轴于点若 , 的面积是 , 则的值为( )
A、2 B、3 C、5 D、76. 如图,在平面直角坐标系中,点、都在反比例函数的图象上,延长交轴于点 , 作轴于点 , 连接、 , 并延长交轴于点若 , 的面积是 , 则的值为( ) A、 B、 C、 D、7. 如图,一次函数与反比例函数的图像相交于A、B两点,与x轴,y轴分别相交于C、D两点,连接OA、OB.过点A作轴于点 , 交于点 . 设点A的横坐标为 . 若 , 则的值为( )
A、 B、 C、 D、7. 如图,一次函数与反比例函数的图像相交于A、B两点,与x轴,y轴分别相交于C、D两点,连接OA、OB.过点A作轴于点 , 交于点 . 设点A的横坐标为 . 若 , 则的值为( ) A、1 B、 C、2 D、48. 与交于A、B两点,交y轴于点C,延长线交双曲线于点D,若 , 则为( )
A、1 B、 C、2 D、48. 与交于A、B两点,交y轴于点C,延长线交双曲线于点D,若 , 则为( )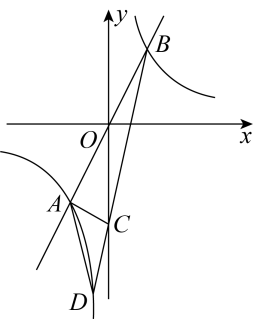 A、2 B、3 C、 D、9. 如图,点 , 分别在轴正半轴、轴正半轴上,以为边构造正方形 , 点 , 恰好都落在反比例函数的图象上,点在延长线上, , , 交轴于点 , 边交反比例函数的图象于点 , 记的面积为 , 若 , 则的面积是( )
A、2 B、3 C、 D、9. 如图,点 , 分别在轴正半轴、轴正半轴上,以为边构造正方形 , 点 , 恰好都落在反比例函数的图象上,点在延长线上, , , 交轴于点 , 边交反比例函数的图象于点 , 记的面积为 , 若 , 则的面积是( ) A、 B、 C、 D、10. 如图,在中,平分交于点C,平分交OA于点D,交于点E,反比例函数 , 经过点E,若 , , 则k的值为( )
A、 B、 C、 D、10. 如图,在中,平分交于点C,平分交OA于点D,交于点E,反比例函数 , 经过点E,若 , , 则k的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,直角坐标系中,▱AOBC的顶点B在x轴的正半轴上,A,C在第一象限.反比例函数(x>0)的图象经过点A,与BC交于点D,AE⊥x轴于点E,连结DE并延长交AO的延长线于点F,反比例函数(x<0)的图象经过点F﹐连结BF,则△BDF的面积为.
 12. 如图所示,点A1 , A2 , A3在x轴上且OA1=A1A2=A2A3 , 分别过点A1 , A2 , A3作y轴的平行线与反比例函数y(k>0,x>0)的图象分别交于点B1 , B2 , B3 , 分别过点B1 , B2 , B3作x轴的平行线分别与y轴交于点C1 , C2 , C3 , 连接OB1 , OB2 , OB3 , 那么图中阴影部分的面积之和为 .
12. 如图所示,点A1 , A2 , A3在x轴上且OA1=A1A2=A2A3 , 分别过点A1 , A2 , A3作y轴的平行线与反比例函数y(k>0,x>0)的图象分别交于点B1 , B2 , B3 , 分别过点B1 , B2 , B3作x轴的平行线分别与y轴交于点C1 , C2 , C3 , 连接OB1 , OB2 , OB3 , 那么图中阴影部分的面积之和为 . 13. 如图,正比例函数的图象与反比例函数的图象交于A , B两点,过点A的直线分别与x轴、y轴交于C , D两点.当 , 时,则 .
13. 如图,正比例函数的图象与反比例函数的图象交于A , B两点,过点A的直线分别与x轴、y轴交于C , D两点.当 , 时,则 .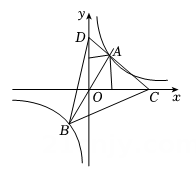 14. 直线y=-x+2a(常数)和双曲线的图象有且只有一个交点B,一次函数y=-x+2a与x轴交于点A,点P是线段OA上的动点,点Q在反比例函数图象上,且满足∠BPO=∠QPA.设PQ与线段AB的交点为M,若OM⊥BP,则的值为 .
14. 直线y=-x+2a(常数)和双曲线的图象有且只有一个交点B,一次函数y=-x+2a与x轴交于点A,点P是线段OA上的动点,点Q在反比例函数图象上,且满足∠BPO=∠QPA.设PQ与线段AB的交点为M,若OM⊥BP,则的值为 . 15. 如图,直线与x轴,y轴交于A、B两点,C为双曲线上一点,连接、 , 且交x轴于点M , , 若的面积为 , 则k的值为 .
15. 如图,直线与x轴,y轴交于A、B两点,C为双曲线上一点,连接、 , 且交x轴于点M , , 若的面积为 , 则k的值为 .
三、解答题
-
16. 如图一次函数 与反比例函数 交于 、 ,与 轴, 轴分别交于点 .
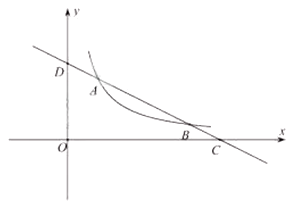 (1)、直接写出一次函数 的表达式和反比例函数 的表达式;(2)、求证: .17. 如图,OA=OB,∠AOB=90°,点A(1,4),B分别在反比例函数和的图象上.
(1)、直接写出一次函数 的表达式和反比例函数 的表达式;(2)、求证: .17. 如图,OA=OB,∠AOB=90°,点A(1,4),B分别在反比例函数和的图象上. (1)、求 k1 , k2的值.(2)、若点 C,D分别在反比例函数和的图象上,且不与点 A,B 重合,则是否存在点 C,D,使得△COD≌△AOB? 若存在,请直接写出点 C,D的坐标;若不存在,请说明理由.18. 如图,直线与双曲线相交于点 , .
(1)、求 k1 , k2的值.(2)、若点 C,D分别在反比例函数和的图象上,且不与点 A,B 重合,则是否存在点 C,D,使得△COD≌△AOB? 若存在,请直接写出点 C,D的坐标;若不存在,请说明理由.18. 如图,直线与双曲线相交于点 , .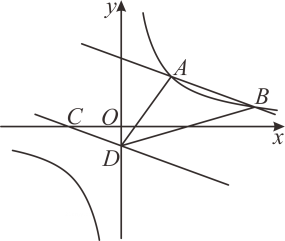 (1)、求双曲线及直线对应的函数表达式;(2)、将直线向下平移至处,其中点 , 点在轴上.连接 , , 求的面积;(3)、请直接写出关于的不等式的解集.19. 如图,一次函数的图象与反比例函数的图象相交于 , 两点,与y轴交于点C .
(1)、求双曲线及直线对应的函数表达式;(2)、将直线向下平移至处,其中点 , 点在轴上.连接 , , 求的面积;(3)、请直接写出关于的不等式的解集.19. 如图,一次函数的图象与反比例函数的图象相交于 , 两点,与y轴交于点C . (1)、求反比例函数和一次函数的解析式;(2)、根据图象直接写出不等式的解集.(3)、设D为线段上的一个动点(不包括A , C两点),过点D作轴交反比例函数图象于点E , 当的面积最大时,求点E的坐标,并求出面积的最大值.20. 如图,一次函数y=kx+b(k≠0)的图象与反比例函数的图象交于点A(﹣2,m)和点B , 与y轴交于点C . 直线x=4经过点B与x轴交于点D , 连结AD .
(1)、求反比例函数和一次函数的解析式;(2)、根据图象直接写出不等式的解集.(3)、设D为线段上的一个动点(不包括A , C两点),过点D作轴交反比例函数图象于点E , 当的面积最大时,求点E的坐标,并求出面积的最大值.20. 如图,一次函数y=kx+b(k≠0)的图象与反比例函数的图象交于点A(﹣2,m)和点B , 与y轴交于点C . 直线x=4经过点B与x轴交于点D , 连结AD . (1)、求k、b的值;(2)、求△ABD的面积;(3)、直接写出一个一次函数的表达式,使它的图象经过点C且y随x的增大而增大.
(1)、求k、b的值;(2)、求△ABD的面积;(3)、直接写出一个一次函数的表达式,使它的图象经过点C且y随x的增大而增大.