2024年中考数学考前20天终极冲刺专题之一次函数
试卷更新日期:2024-05-20 类型:三轮冲刺
一、选择题
-
1. 下列不能表示y是x的函数的是( )A、
 B、
B、 C、
C、 D、
2. 一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列函数中,自变量x的取值范围是x>1的函数是( )A、 B、 C、y=x﹣1 D、4. 如图,某蓄水池的横断面示意图,如果这个蓄水池以固定的流量注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系( )
D、
2. 一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列函数中,自变量x的取值范围是x>1的函数是( )A、 B、 C、y=x﹣1 D、4. 如图,某蓄水池的横断面示意图,如果这个蓄水池以固定的流量注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系( )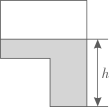 A、
A、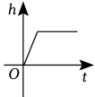 B、
B、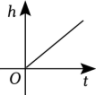 C、
C、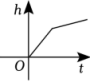 D、
D、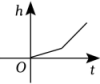 5. 已知为常数,且 , 一次函数的图象不经过第三象限,则正比例函数的图象经过的象限是( )A、第一、三象限 B、第二、四象限 C、第一、二象限 D、第三、四象限6. 武汉作为新晋网红城市,五一期间吸引着大量游客前来观光打卡.现有一批游客分别乘坐甲乙两辆旅游大巴同时从旅行社前往某个旅游景点.行驶过程中甲大巴因故停留一段时间后继续驶向景点,乙大巴全程匀速驶向景点.两辆大巴的行程随时间变化的图象(全程)如图所示.依据图中信息,下列说法错误的是( )
5. 已知为常数,且 , 一次函数的图象不经过第三象限,则正比例函数的图象经过的象限是( )A、第一、三象限 B、第二、四象限 C、第一、二象限 D、第三、四象限6. 武汉作为新晋网红城市,五一期间吸引着大量游客前来观光打卡.现有一批游客分别乘坐甲乙两辆旅游大巴同时从旅行社前往某个旅游景点.行驶过程中甲大巴因故停留一段时间后继续驶向景点,乙大巴全程匀速驶向景点.两辆大巴的行程随时间变化的图象(全程)如图所示.依据图中信息,下列说法错误的是( ) A、甲大巴停留前的平均速度是 B、甲大巴中途停留了0.5h C、甲大巴比乙大巴先0.25h到达景点 D、甲大巴停留后用0.5h追上乙大巴7. 如图,点G是的中点,点H在上,动点P以每秒的速度沿图1的边线运动,运动路径为: , 相应的的面积关于运动时间的函数图象如图2,若 , 则下列六个结论中正确的个数有( )
A、甲大巴停留前的平均速度是 B、甲大巴中途停留了0.5h C、甲大巴比乙大巴先0.25h到达景点 D、甲大巴停留后用0.5h追上乙大巴7. 如图,点G是的中点,点H在上,动点P以每秒的速度沿图1的边线运动,运动路径为: , 相应的的面积关于运动时间的函数图象如图2,若 , 则下列六个结论中正确的个数有( )
①图1中的长是;
②图2中的M点表示第4秒时y的值为;
③图1中的长是;
④图1中的长是;
⑤图2中的Q点表示第8秒时y的值为33;
⑥图2中的N点表示第12秒时y的值为 .
A、3个 B、4个 C、5个 D、6个8. 如图,点A , B , C在一次函数的图象上,它们的横坐标依次为 , , , 分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( ) A、 B、 C、 D、9. 在同一平面直角坐标系中,一次函数与的图象可能是( )A、
A、 B、 C、 D、9. 在同一平面直角坐标系中,一次函数与的图象可能是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在中, , , , 点P从点A出发沿的路径运动到点C停止,点Q以相同的速度沿的路径运动到点C停止,连接 , 设点P的运动路程为x,的面积为y,则下列图象能大致反映y与x之间的函数关系的是( )
10. 如图,在中, , , , 点P从点A出发沿的路径运动到点C停止,点Q以相同的速度沿的路径运动到点C停止,连接 , 设点P的运动路程为x,的面积为y,则下列图象能大致反映y与x之间的函数关系的是( )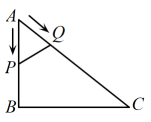 A、
A、 B、
B、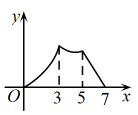 C、
C、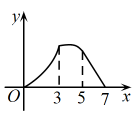 D、
D、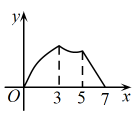
二、填空题
-
11. 如图,直线(k为常数,)与x,y轴分别交于点A,B,则的值是 .
 12. 如图,直线AB经过原点O,点C在y轴上,D为线段AB上一动点,若A(2,m),B(-3,n),C(0,-2),AB=10,则CD长度的最小值为.
12. 如图,直线AB经过原点O,点C在y轴上,D为线段AB上一动点,若A(2,m),B(-3,n),C(0,-2),AB=10,则CD长度的最小值为. 13. 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过正方形OABC的顶点A和C,已知点A的坐标为(1,﹣3),则一次函数的解析式为 .
13. 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过正方形OABC的顶点A和C,已知点A的坐标为(1,﹣3),则一次函数的解析式为 . 14. 如图,直线分别与x、y轴交于点A、B , 点C在线段上,线段沿翻折,点O落在边上的点D处.则直线的解析式为 .
14. 如图,直线分别与x、y轴交于点A、B , 点C在线段上,线段沿翻折,点O落在边上的点D处.则直线的解析式为 . 15. 如图,直线与直线交于点 , 则关于x的不等式的解集是.
15. 如图,直线与直线交于点 , 则关于x的不等式的解集是.
三、解答题
-
16. 2024年春节的“文旅热”现象,展现着我国经济的强大韧性.今年春节长假后,陕西某地深入复盘总结,坚持“以文塑旅、以旅彰文”的方法路径,不断提供优质文旅产品,做强地方文化“软实力”、文旅资源“硬支撑”,引导文旅业态健康发展.苏晓一家前往陕西某景点旅游,他们从家出发,匀速行驶后进入高速,在高速路上匀速行驶一段时间后,驶出高速,进入城市道路(城市道路的行驶速度低于高速路上的行驶速度),苏晓一家离家的距离与行驶时间之间的函数关系如图所示,请根据图中信息,解答下列问题:
 (1)、苏晓一家在高速路上行驶的时间是小时;(2)、求图中段与之间的函数表达式;(3)、苏晓一家从家出发多久后,离家的距离为?17. 在测浮力的实验中,下方为盛水的烧杯,上方有弹簧测力计悬挂的圆柱体,将圆柱体缓慢下降,直至圆柱体完全浸入水中,各种状态如图甲所示,其中,弹簧测力计在状态②和④显示的读数分别为和 . 整个过程中,弹簧测力计读数F与圆柱体下降高度h的关系图象如图乙所示.
(1)、苏晓一家在高速路上行驶的时间是小时;(2)、求图中段与之间的函数表达式;(3)、苏晓一家从家出发多久后,离家的距离为?17. 在测浮力的实验中,下方为盛水的烧杯,上方有弹簧测力计悬挂的圆柱体,将圆柱体缓慢下降,直至圆柱体完全浸入水中,各种状态如图甲所示,其中,弹簧测力计在状态②和④显示的读数分别为和 . 整个过程中,弹簧测力计读数F与圆柱体下降高度h的关系图象如图乙所示. (1)、图乙中,点A对应状态 , 点B对应状态 , (“状态”后填写图形序号)
(1)、图乙中,点A对应状态 , 点B对应状态 , (“状态”后填写图形序号), ;
(2)、已知弹簧测力计在状态③时显示的读数为 , 求圆柱体浸入水中的高度.四、综合题
-
18. 如图,已知直线与x轴交于点A,与y轴交于点B,点M是线段AB的中点,点P为x轴负半轴上一动点,点P的横坐标记作m,过点A作AQ∥BP交PM的延长线于Q,PM交y轴于点C,连接OM.
 (1)、线段OM的长;(2)、①证明:四边形AQBP是平行四边形;
(1)、线段OM的长;(2)、①证明:四边形AQBP是平行四边形;②当m取何值时,四边形AQBP是菱形;
(3)、若点M坐标为(3,4),当﹣3≤m≤﹣2时,记(其中OC示线段OC的长度),求s的最大值.19. 如图,在平面直角坐标系中,过点A(﹣6,0)的直线l1:y1=kx+b(k≠0)与直线l2:y2=2x相交于B(m,4). (1)、求直线l1的函数解析式;(2)、设直线l1与y轴交于点M,求△BOM的面积;(3)、利用函数图象直接写出当y1≤y2时,x的取值范围为 .20. 如图,正方形AOBC的边长为2,点O为坐标原点,边OB,OA分别在x轴,y轴上,点D是BC的中点,点P是线段AC上的一个点,如果将OA沿直线OP对折,使点A的对应点A'恰好落在PD所在的直线上.
(1)、求直线l1的函数解析式;(2)、设直线l1与y轴交于点M,求△BOM的面积;(3)、利用函数图象直接写出当y1≤y2时,x的取值范围为 .20. 如图,正方形AOBC的边长为2,点O为坐标原点,边OB,OA分别在x轴,y轴上,点D是BC的中点,点P是线段AC上的一个点,如果将OA沿直线OP对折,使点A的对应点A'恰好落在PD所在的直线上. (1)、连接OD,求证:△A'OD≌△BOD;(2)、利用你所学的数学知识求出折痕OP所在直线的函解式;(3)、请问x轴上是否存在一点,使△DPQ的周长有最小值?若存在,请求出点Q的坐标;若不存在,请说明理由.21. 如图,平面直角坐标系中, , . F为矩形OABC对角线AC的中点,过点F的直线分别与OC、AB交于点D、E .
(1)、连接OD,求证:△A'OD≌△BOD;(2)、利用你所学的数学知识求出折痕OP所在直线的函解式;(3)、请问x轴上是否存在一点,使△DPQ的周长有最小值?若存在,请求出点Q的坐标;若不存在,请说明理由.21. 如图,平面直角坐标系中, , . F为矩形OABC对角线AC的中点,过点F的直线分别与OC、AB交于点D、E . (1)、求证:;(2)、设 , 的面积为S , 求S与m的函数关系式;(3)、若点P在坐标轴上,平面内存在点Q , 使以P、Q、A、C为顶点的四边形是矩形,请直接写出点Q的坐标.22. 如图,矩形的顶点A、C分别在x轴、y轴的正半轴上,点B的坐标为 , 一次函数的图象与边、分别交于点D、E , 且 . 点M是线段上的一个动点.
(1)、求证:;(2)、设 , 的面积为S , 求S与m的函数关系式;(3)、若点P在坐标轴上,平面内存在点Q , 使以P、Q、A、C为顶点的四边形是矩形,请直接写出点Q的坐标.22. 如图,矩形的顶点A、C分别在x轴、y轴的正半轴上,点B的坐标为 , 一次函数的图象与边、分别交于点D、E , 且 . 点M是线段上的一个动点. (1)、求b的值;(2)、连接 , 若三角形的面积与四边形的面积之比为 , 求点M的坐标;(3)、设点N是平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.
(1)、求b的值;(2)、连接 , 若三角形的面积与四边形的面积之比为 , 求点M的坐标;(3)、设点N是平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.