2024中考数学考前20天终极冲刺专题之数与式

试卷更新日期：2024-05-20 类型：三轮冲刺

进入出卷网下载

一、选择题

1. 下列各组数中，比0小的数是（）

A、5 B、 $\frac{1}{5}$ C、0 D、-5

查看试题解析
2. 尼莫点，正式名称为海洋难抵极，是地球表面距离陆地最偏远的地点，位于南太平洋中央的海面上，最近的陆地与当地相隔2688000米之遥，其中2688000用科学记数法表示应为（）

A、2.688×10⁷ B、26.88×10⁵ C、2.688×10⁶ D、0.2688×10⁷

查看试题解析
3. 下列运算正确的是（）

A、a²•a³＝a⁶ B、（a³）²＝a⁵ C、（3ab²）³＝9a³b⁶ D、a⁶÷a²＝a⁴

查看试题解析
4. 若代数式 $\frac{1}{\sqrt{2 x - 6}}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x \geq - 3$ B、 $x > - 3$ C、 $x \geq 3$ D、 $x > 3$

查看试题解析
5. 已知多项式ax+b与2x²﹣x+2的乘积展开式中不含x的一次项，且常数项为﹣4，则a^b的值为（）

A、﹣2 B、2 C、﹣1 D、1

查看试题解析
6. 已知x²+y²+4x﹣6y+13=0，则代数式x+y的值为（）

A、﹣1 B、1 C、25 D、36

查看试题解析
7. 下列式子中是最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{4}$ C、 $\sqrt{5}$ D、 $\sqrt{12}$

查看试题解析
8. 照相机成像应用了一个重要原理，用公式 $\frac{1}{f} = \frac{1}{u} + \frac{1}{v} (v \neq f)$ 表示，其中f表示照相机镜头的焦距，u表示物体到镜头的距离，v表示胶片（像）到镜头的距离．已知f，v，则u＝（）

A、 $\frac{f v}{f - v}$ B、 $\frac{f - v}{f v}$ C、 $\frac{f v}{v - f}$ D、 $\frac{v - f}{f v}$

查看试题解析
9. $2 ， 5 ， m$ 是某三角形三边的长，则 $\sqrt{{(m - 3)}^{2}} + \sqrt{{(m - 7)}^{2}}$ 等于（）

A、 $2 m - 10$ B、 $10 - 2 m$ C、10 D、4

查看试题解析
10. 已知 $2 5^{x} = a$ ， $5^{y} = b$ ， $12 5^{z} = a b$ ，那么x，y，z满足的等量关系是（）

A、 $2 x + y = z$ B、 $x y = 3 z$ C、 $2 x + y = 3 z$ D、 $2 x y = z$

查看试题解析

二、填空题

11. $\sqrt{81}$ 的算术平方根是

查看试题解析
12. 把多项式 $m x^{2} - 16 m$ 分解因式的结果是．

查看试题解析
13. 若x+y+z=2，x²﹣（y+z）²=8时，x﹣y﹣z= ．

查看试题解析
14. 若 $(x + 3) (x - 5) = x^{2} + m x - 15$ ，则 $m =$ .

查看试题解析
15. 已知数轴上A、B两个点之间的距离是 $3 \sqrt{5}$ ，点A所对应的实数是 $- \frac{\sqrt{5}}{2}$ ，那么点B所对应的实数是．

查看试题解析
16. 已知a、b为两个连续整数，且 $a < \sqrt{15} < b$ ，则a+b的值为．

查看试题解析

三、计算题

17. 计算： $\sqrt{4} + | - 2 | - \sqrt{3} t a n 3 0^{°} - {(\frac{1}{2024})}^{0}$ .

查看试题解析
18. 先化简 $\frac{x^{2} - 2 x + 1}{x^{2} - 1} \div (\frac{x - 1}{x + 1} - x + 1)$ ，然后从 $- \sqrt{6} < x < \sqrt{6}$ 的范围内选取一个你喜欢的合适的整数作为x的值代入求值.

查看试题解析

四、解答题

19. 阅读下列简化过程：
$\frac{1}{\sqrt{2} + 1} = \frac{(\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；
$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{(\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；
$\frac{1}{\sqrt{4} + \sqrt{3}} = \frac{(\sqrt{4} - \sqrt{3})}{(\sqrt{4} + \sqrt{3}) (\sqrt{4} - \sqrt{3})} = \sqrt{4} - \sqrt{3}$ ．
解答下列问题：

(1)、直接写出结果 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ ；

(2)、计算： $\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + 2} + . . . . . + \frac{1}{\sqrt{2021} + \sqrt{2022}}$ ；

(3)、设 $a = \frac{1}{\sqrt{3} - \sqrt{2}}$ ， $b = \frac{1}{2 - \sqrt{3}}$ ， $c = \frac{1}{\sqrt{5} - 2}$ ，比较 $a$ ， $b$ ， $c$ 的大小关系．

查看试题解析
20. 先阅读理解下面的例题，再按要求解答下列问题：
例题：解一元二次不等式 $x^{2} - 4 > 0$ .
解： $∵ x^{2} - 4 = (x + 2) (x - 2)$ ，
$∴ x^{2} - 4 > 0$ 可化为 $(x + 2) (x - 2) > 0$ .
由有理数的乘法法则“两数相乘，同号得正”，得
① ${\begin{array}{l} x + 2 > 0 \\ x - 2 > 0 \end{array}$ ， ② ${\begin{array}{l} x + 2 < 0 \\ x - 2 < 0 \end{array}$ ，
解不等式组①，得 $x > 2$ ，解不等式组②，得 $x < - 2$ ，
$∴ (x + 2) (x - 2) > 0$ 的解集为 $x > 2$ 或 $x < - 2$ ，
即一元二次不等式 $x^{2} - 4 > 0$ 的解集为 $x > 2$ 或 $x < - 2$ .

(1)、一元二次不等式 $x^{2} - 16 > 0$ 的解集为；

(2)、分式不等式 $\frac{x - 1}{x - 3} > 0$ 的解集为；

(3)、解一元二次不等式 $2 x^{2} - 5 x < 0$ .

查看试题解析

五、实践探究题

21. 用几个小的长方形、正方形拼成一个大的正方形，然后利用两种不同的方法计算这个大的正方形的面积，可以得到一个等式．例如：计算图1的面积，把图1看作一个大正方形，它的面积是 ${(a + b)}^{2}$ ；如果把图1看作是由2个长方形和2个小正方形组成的，它的面积为 $a^{2} + 2 a b + b^{2}$ ，由此得到 ${(a ＋ b)}^{2} = a^{2} + 2 a b + b^{2}$ ．

(1)、如图2，由几个面积不等的小正方形和几个小长方形拼成一个边长为 $(a + b + c)$ 的正方形，
从中你能发现什么结论？该结论用等式表示为；

(2)、利用（1）中的结论解决以下问题：
①已知 $a + b + c = 10$ ， $a b + a c + b c = 38$ ，求 $a^{2} + b^{2} + c^{2}$ 的值；
②如图3，由正方形 $A B C D$ 边长为a ，正方形 $C E F G$ 边长为b ，点 $D, G, C$ 在同一直线上，连接 $B D ， D F$ ，
若 $a - b = 2 ， a b = 3$ ，求图3中阴影部分的面积．

查看试题解析
22. 阅读材料：若 $x$ 满足 $(6 - x) (x - 4) = 3$ ，求 ${(6 - x)}^{2} + {(x - 4)}^{2}$ 的值．
解：设 $(6 - x) = a$ ， $(x - 4) = b$ ，则 $(6 - x) (x - 4) = a b = 3$ ， $a + b = (6 - x) + (x - 4) = 2$
所以 ${(6 - x)}^{2} + {(x - 4)}^{2} = a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = 2^{2} - 2 \times 3 = - 2$
请仿照上例解决下列问题：

(1)、若x满足 $(20 - x) (x - 10) = - 5$ ，求 ${(20 - x)}^{2} + {(x - 10)}^{2}$ 的值；

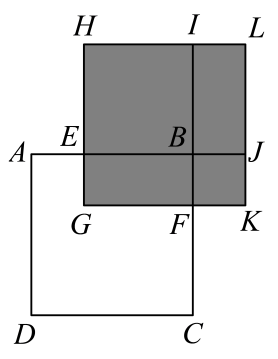
(2)、若x满足 ${(2023 - x)}^{2} + {(2021 - x)}^{2} = 2022$ ，求 $(2023 - x) (2021 - x)$ 的值；

(3)、如图，正方形 $A B C D$ 的边长为 $x$ ， $A E = 2$ ， $F C = 4$ ，长方形 $E B F G$ 的面积是10，四边形 $H I B E$ 和 $B J K F$ 都是正方形， $I L J B$ 是长方形，求图中阴影部分的面积（结果必须是一个具体的数值）．

查看试题解析