浙江省宁波市鄞州区2023学年七年级下册数学期中试卷

试卷更新日期：2024-05-20 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 下列运算正确的是（）

A、a²•a³＝a⁶ B、（a³）²＝a⁵ C、（3ab²）³＝9a³b⁶ D、a⁶÷a²＝a⁴

查看试题解析
2. 若 ${\begin{matrix} x = - 1 \\ y = 2 \end{matrix}$ 是关于x．y的方程2x﹣y+2a=0的一个解，则常数a为（）

A、1 B、2 C、3 D、4

查看试题解析
3. 世界上最小、最轻的昆虫是膜翅缨小蜂科的一种卵蜂，其质量只有0.000005克，0.000005用科学记数法表示是（）

A、5×10^-6 B、5×10^-5 C、5×10^-4 D、5×10^-3

查看试题解析
4. 如图，直线a∥b，∠1＝120°，则∠2的度数是（）

A、120° B、80° C、60° D、50°

查看试题解析
5. 如图所示，在下列四组条件中，能判定 $A B ∥ C D$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ A B D = ∠ B D C$ C、 $∠ 3 = ∠ 4$ D、 $∠ B A D + ∠ A B C = 180 °$

查看试题解析
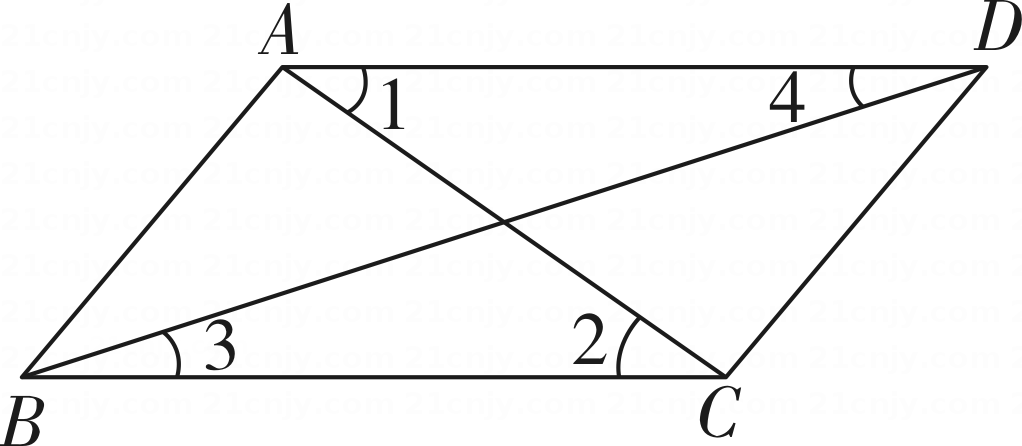6. 下列代数式变形中，是因式分解的是（）

A、 $\frac{16}{3} a_{}^{6}$ B、 $1 - 3 a$ C、 $x_{}^{2} - 3 x + 1 = x (x - 3) + 1$ D、 $- x_{}^{2} + 2 x - 1 = - (x - 1)_{}^{2}$

查看试题解析
7. 计算 $(a - b) (a + b) (a_{}^{2} - b_{}^{2})$ 的结果是（）

A、a⁴-2a²b²+b⁴ B、 $a_{}^{4} + 2 a_{}^{2} b_{}^{2} + b_{}^{4}$ C、 $a_{}^{4} + b_{}^{4}$ D、 $a_{}^{4} － b_{}^{4}$

查看试题解析
8. 80³-80能被（　　）整除．

A、76 B、78 C、79 D、82

查看试题解析
9. 已知x²+y²+4x﹣6y+13=0，则代数式x+y的值为（）

A、﹣1 B、1 C、25 D、36

查看试题解析
10. 已知多项式ax+b与2x²﹣x+2的乘积展开式中不含x的一次项，且常数项为﹣4，则a^b的值为（）

A、﹣2 B、2 C、﹣1 D、1

查看试题解析

二、填空题：（每小题3分，共24分）

11. 分解因式a²﹣9a的结果是

查看试题解析
12. 将方程3x+2y=7变形成用含y的代数式表示x，得到.

查看试题解析
13. 如图，AB∥EF∥CD，∠ABC=46°，∠BCE=20°，则∠CEF= ．

查看试题解析
14. 如图，将△ABC平移到△A^'B^'C^'的位置（点B^'在AC边上），若∠B=55°，∠C=100°，则∠AB^'A^'的度数为°

查看试题解析
15. 计算：（﹣π）⁰+2^-2= ．

查看试题解析
16. 若x+y+z=2，x²﹣（y+z）²=8时，x﹣y﹣z= ．

查看试题解析
17. 若x+2y﹣3=0，则2^x•4^y的值为．

查看试题解析
18. 求1+2+2²+2³+…+2²⁰¹²的值，可令S=1+2+2²+2³+…+2²⁰¹² ，则2S=2+2²+2³+2⁴+…+2²⁰¹³ ，因此2S－S=2²⁰¹³－1．仿照以上推理，计算出1+5+5²+5³+…+5²⁰¹²的值为.

查看试题解析

三、解答题：（共46分）

19. 化简：

(1)、（2a²）⁴÷3a²

(2)、（1+a）（1-a）+a（a-3）

查看试题解析
20. 解下列二元一次方程组：

(1)、 ${\begin{cases} 3 x - y = 2 \\ 9 x + 8 y = 17 \end{cases}$

(2)、 ${\begin{cases} 2 x - 3 y = 4 \\ 5 x - 3 y = 19 \end{cases}$

查看试题解析
21. 已知 $a - b = 7$ ， $a b = - 12$ ．

(1)、求 $a_{}^{2} b - a b_{}^{2}$ 的值；

(2)、求 $a_{}^{2} + b_{}^{2}$ 的值；

(3)、求 $a + b$ 的值；

查看试题解析
22. 如图，已知∠1=∠2，∠B=∠C，可推得AB∥CD．请说明理由

查看试题解析
23. 小刚同学动手剪了如图①所示的正方形与长方形纸片若干张．

(1)、他用1张1号、1张2号和2张3号卡片拼出一个新的图形（如图②）．根据这个图形的面积关系写出一个你所熟悉的乘法公式，这个乘法公式是；

(2)、如果要拼成一个长为（a+2b），宽为（a+b）的大长方形，则需要2号卡片张，3号卡片张；

(3)、当他拼成如图③所示的长方形，根据6张小纸片的面积和等于大纸片（长方形）的面积可以把多项式a²+3ab+2b²分解因式，其结果是；

(4)、动手操作，请你依照小刚的方法，画出拼图并利用拼图分解因式a²+5ab+6b²= ▲ ．

查看试题解析
24. 某商店决定购进A、B两种纪念品，若购进A种纪念品10件，B种纪念品5件，需要2000元；若购进A种纪念品5件，B种纪念品3件，需要1050元．

(1)、求购进A、B两种纪念品每件各需多少元？

(2)、若该商店决定拿出4000元全部用来购进这两种纪念品，其中各纪念品至少购进12件，那么该商店共有几种进货方案？

(3)、若销售每件A种纪念品可获利润20元，每件B种纪念品可获利润30元，在第（2）问的各种进货方案中，哪一种方案获利最大？最大利润是多少？

查看试题解析