浙江省杭州市临平区2023-2024学年七年级下学期数学期中试卷

试卷更新日期：2024-05-20 类型：期中考试

进入出卷网下载

一、选择题：本大题有10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项最符合题目要求．

1. 点点同学读了“子非鱼焉知鱼之乐乎?”后，兴高采烈地利用电脑画出了几幅鱼的图案，请问：由左图所示的图案平移后得到的图案是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（）

A、 $x^{2} + x^{3} = x^{5}$ B、 $x^{2} \cdot x^{3} = x^{6}$ C、 ${(x^{2})}^{3} = x^{5}$ D、 ${(2 x^{3})}^{2} = 4 x^{6}$

查看试题解析
3. 下列方程中，是二元一次方程的是（）

A、 $3 x - 2 y = 4 z$ B、 $6 x y + 9 = 0$ C、 $x + 4 y = 6$ D、 $x = \frac{2}{y} + 1$

查看试题解析
4. 下列各组数中，是二元一次方程 $5 x - y = 2$ 的一个解的是（）

A、 ${\begin{array}{l} x = 3 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 0 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = 0 \end{array}$ D、 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$

查看试题解析
5. 下列多项式的乘法中，能用平方差公式计算的是（）

A、 $(\frac{1}{2} a + b) (b - \frac{1}{2} a)$ B、 $(- m + n) (m - n)$ C、 $(x + 5) (x + 5)$ D、 $(3 a - 4 b) (3 b + 4 a)$

查看试题解析
6. 如图， $A B / / D E$ ，若 $∠ A C D = 5 5^{°}$ ，则 $∠ A$ 等于（）

A、 $3 5^{°}$ B、 $5 5^{°}$ C、 $6 5^{°}$ D、 $12 5^{°}$

查看试题解析
7. 若 $x^{2} - 2 m x + 9$ 是关于 $x$ 的完全平方式，则 $m$ 的值为（）

A、 $\pm 3$ B、 $\pm 6$ C、3 D、6

查看试题解析
8. 如图所示，把一块三角板的直角顶点放在直尺的一边上，若 $∠ 1 = 3 2^{°}$ ，则 $∠ 2$ 的度数是（）

A、 $3 2^{°}$ B、 $5 8^{°}$ C、 $6 8^{°}$ D、 $6 0^{°}$

查看试题解析
9. 用白铁皮做罐头盒，每张铁皮可制盒身25个，或制盒底40个，一个盒身与两个盒底配成一套罐头盒．现有36张白铁皮，设用 $x$ 张制盒身， $y$ 张制盒底，恰好配套制成罐头盒，则下列方程组中符合题意的是（）

A、 ${\begin{array}{l} x + y = 36 \\ y = 2 x \end{array}$ B、 ${\begin{array}{l} x + y = 36 \\ x = 2 y \end{array}$ C、 ${\begin{array}{l} x + y = 36 \\ 2 \times 25 x = 40 y \end{array}$ D、 ${\begin{array}{l} x + y = 36 \\ 25 x = 2 \times 40 y \end{array}$

查看试题解析
10. 已知关于 $x$ 和 $y$ 的方程组 ${\begin{array}{l} 2 x - y = 3 k - 2 \\ 2 x + y = 4 - k \end{array}$ （ $k$ 为常数），下列结论正确的个数为（）
①无论 $k$ 取何值，都有 $4 x + y = 5$ ；②若 $k = 1$ ，则 $(2 x - 1) y = 1$
③方程组有非负整数解时， $k = 1$ ；④若 $x$ 和 $y$ 互为相反数，则 $k = \frac{7}{3}$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题：本大题有6个小题，每小题3分，共18分．

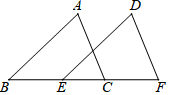
11. 已知 $a - 5 b = 2$ ，用含 $b$ 的代数式表示 $a$ ，则 $a =$ .

查看试题解析
12. 如图，将 $△ A B C$ 向右平移5个单位长度得到 $△ D E F$ ，且点B，E，C，F在同一条直线上，若 $E C = 3$ ，则 $B C$ 的长度是．

查看试题解析
13. 若 $(x + 3) (x - 5) = x^{2} + m x - 15$ ，则 $m =$ .

查看试题解析
14. 已知 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ 是二元一次方程 $a x + b y = - 1$ 的一组解，则 $2 a - b + 2024 =$ .

查看试题解析
15. 已知 $m + 2 n - 2 = 0$ ，则 $3^{m} \cdot 9^{n}$ 的值为.

查看试题解析
16. 如图1，将一条两边互相平行的长方形纸带沿EF折叠，设 $∠ A E D^{^{'}} = x$ 度．

(1)、若 $x = 11 0^{°}$ 。则 $∠ E F B =$ 度．

(2)、将图1纸带继续沿BF折叠成图2，则 $∠ E F C^{^{'}^{'}} =$ 度．（用含 $x$ 的代数式表示）

查看试题解析

三、解答题：本大题有8个小题，共72分．解答应写出文字说明、证明过程或演算步骤．

17. 计算：

(1)、 $- 3 a \cdot (2 b)$

(2)、 ${(4 a^{2} b)}^{2} \div (8 a^{2})$

查看试题解析
18. 先化简，再求值：
$(x - 2 y)^{2} - (x + y) (x - y)$ ，其中 $x = \frac{1}{2}, y = 1$ ．

查看试题解析
19. 解方程组：

(1)、 ${\begin{array}{l} 2 x - 3 y = 1 ① \\ 3 x + y = 7 ② \end{array}$

(2)、 ${\begin{array}{l} x + 1 = 3 y ① \\ 2 (x + 1) - y = 8 ② \end{array}$

查看试题解析
20. 如图，在 $7 \times 7$ 的网格中，A，B，C，D均在格点上，按下列要求作图：

(1)、在图1中，找出格点E，连结DE，使得DE//BC.

(2)、在图2中，平移△ABC得到 $△ A^{^{'}} B^{^{'}} C^{^{'}}$ ，使得点 $D$ 为 $△ A^{^{'}} B^{^{'}} C^{^{'}}$ 一边的中点，请画出 $△ A^{^{'}} B^{^{'}} C^{^{'}}$ ．

查看试题解析
21. 如图，在 $△ A B C$ 中， $C D ⊥ A B$ 于点 $D$ ，点 $E$ 是BC上一点，过点 $E$ 作 $E F ⊥ A B$ 于点 $F$ ，点 $G$ 是AC上一点，且 $∠ 1 = ∠ 2$ ．

(1)、请说明 $D G / / B C$ 的理由．

(2)、若 $∠ 3 = 7 0^{°}, C D$ 平分 $∠ A C B$ ，求 $∠ 2$ 的度数．

查看试题解析
22. 完全平方公式经过适当的变形，可以解决很多数学问题．
例如：若 $a + b = 3, a b = 1$ ，求 $a^{2} + b^{2}$ 的值．
解： $∵ a + b = 3, a b = 1$ ，
$∴ (a + b)^{2} = 9, 2 a b = 2 .$
$∴ a^{2} + b^{2} + 2 a b = 9,$
$∴ a^{2} + b^{2} = 7 .$
根据上面的解题思路与方法解决下列问题：

(1)、若 $(9 - x) (x - 6) = 1$ ，求 $(9 - x)^{2} + (x - 6)^{2}$ 的值.

(2)、如图， $C$ 是线段AB上的一点，分别以AC，BC为边向两边作正方形，设 $A B = 6$ ，两正方形的面积和为20，求 $△ A F C$ 的面积．

查看试题解析
23. 综合与实践
问题情境：“综合与实践”课上，老师将一副直角三角板摆放在直线MN上（如图1， $∠ E D C = 9 0^{°}, ∠ D E C = 6 0^{°}, ∠ A B C = 9 0^{°}, ∠ B A C = 4 5^{°}$ ）．保持三角板EDC不动，老师将三角板ABC绕点 $C$ 以每秒 $5^{°}$ 的速度顺时针旋转，旋转时间为 $t$ 秒，当AC与射线CN重合时停止旋转．各小组解决老师给出的问题，又提出新的数学问题，请你解决这些问题.
深入探究：

(1)、老师提出，如图2，当AC转到与∠DCE的角平分线重合时，∠ECB-∠DCA=15°，当AC转到与 $∠ D C E$ 的角平分线重合时， $∠ E C B - ∠ D C A = 1 5^{°}$ ，当AC在 $∠ D C E$ 内部的其他位置时，结论 $∠ E C B - ∠ D C A = 1 5^{°}$ 是否依然成立?请说明理由．

(2)、勤学小组提出：若AC旋转至 $∠ D C E$ 的外部， $∠ D C A$ 与 $∠ E C B$ 是否还存在如上数量关系?若存在，请说明理由；若不存在，请写出 $∠ D C A$ 与 $∠ E C B$ 的数量关系，并说明理由．

(3)、拓展提升：
智慧小组提出：若AC旋转到与射线CM重合时停止旋转．在旋转过程中，直线DE与直线AC是否存在平行的位置关系?若存在，请直接写出 $t$ 的值；若不存在，请说明理由．

查看试题解析
24. 某公司后勤部准备去超市采购牛奶和咖啡若干箱，现有两种不同的购买方案，如下表：

牛奶（箱
咖啡（箱）
金额（元）
方案一
20
10
110
方案二
30
15

(1)、采购人员不慎将污渍弄到表格上，根据表中的数据，判断污渍盖住地方对应金额是元；

(2)、若后勤部计划购买牛奶25箱，咖啡20箱，需支付金额1750元，求牛奶与咖啡每箱分别多少元?

(3)、在（2）的单价下，部分牛奶和咖啡因保质期临近，进行打六折的促销活动，后勤部根据需要选择原价或打折的牛奶和咖啡，此次采购共花费了1200元，其中购买打折的牛奶箱数是所有牛奶、咖啡的总箱数的 $\frac{1}{4}$ ．求此次按原价采购的咖啡的箱数．

查看试题解析

	牛奶（箱	咖啡（箱）	金额（元）
方案一	20	10	110
方案二	30	15