湖南省湘潭市岳塘区四校联考2023-2024学年九年级下学期数学期中试卷

试卷更新日期：2024-05-20 类型：期中考试

进入出卷网下载

一、选择题：本题共10小题，每小题4分，共40分。在每小题给出的选项中，只有一项是符合题目要求的。

1. 实数 $a$ ， $b$ 在数轴上的对应点的位置如图所示，下列结论正确的是( )

A、 $| a | < | b |$ B、 $a - b > 0$ C、 $a + b < 0$ D、 $a b > 0$

查看试题解析
2. 下列几何体中，主视图和左视图都为矩形的是( )

A、球 B、直立圆柱 C、圆锥 D、倒放圆柱

查看试题解析
3. 某球员参加一场篮球比赛，比赛分4节进行，该球员每节得分如折线统计图所示，则该球员平均每节得分为（）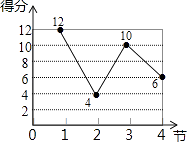

A、7分 B、8分 C、9分 D、10分

查看试题解析
4. 已知关于x的方程2x－a ＋5 ＝ 0的解是x＝2，则a的值为（）

A、6 B、7 C、8 D、9

查看试题解析
5. 如图， $△ A B C$ 与 $△ D E F$ 是位似图形，点 $O$ 为位似中心，位似比为 $2$ ： $3 .$ 若 $△ A B C$ 的面积为 $8$ ，则 $△ D E F$ 的面积是( )

A、 $15$ B、 $16$ C、 $9$ D、 $18$

查看试题解析
6. 如图所示，要在一条公路的两侧铺设平行管道，现在要将两侧的管道对接，如果一侧铺设的角度为 $120 °$ ，那么另一侧铺设的角度大小应为( )

A、 $120 °$ B、 $100 °$ C、 $80 °$ D、 $60 °$

查看试题解析
7. 若点 $(- 2,3)$ 在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 图象上，则该函数图象一定经过点( )

A、 $(3,2)$ B、 $(- 3,2)$ C、 $(- 3, - 2)$ D、 $(- 2, - 3)$

查看试题解析
8. 对于两个不相等的实数 $a$ 、 $b$ ，我们规定符号 $M a x {a, b}$ 表示 $a$ 、 $b$ 中的较大值，如： $M a x {2,4} = 4$ ，按照这个规定，方程 $M a x {x, - x} = \frac{2 x + 1}{x}$ 的解为( )

A、 $1 - \sqrt{2}$ B、 $2 - \sqrt{2}$ C、 $1 + \sqrt{2}$ 或 $1 - \sqrt{2}$ D、 $1 + \sqrt{2}$ 或 $- 1$

查看试题解析
9. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ， $A B = A D$ ， $∠ B C D = 120 °$ ， $E$ 、 $F$ 分别为 $B C$ 、 $C D$ 上一点， $∠ E A F = 30 °$ ， $E F = 3$ ， $D F = 1 .$ 则 $B E$ 的长为( )

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c$ ，其中 $y$ 与 $x$ 的部分对应值如表：

$x$

$- 2$

$- 1$

$0.5$

$1.5$

$y$

$5$

$0$

$- 3.75$

$- 3.75$
下列结论正确的是( )

A、 $a b c < 0$ B、 $4 a + 2 b + c > 0$ C、若 $x < - 1$ 或 $x > 3$ 时， $y > 0$ D、方程 $a x^{2} + b x + c = 5$ 的解为 $x_{1} = - 2$ ， $x_{2} = 3$

查看试题解析

二、填空题：本题共6小题，每小题4分，共24分。

11. 分解因式： $2 x^{2} y + 4 y =$ ．

查看试题解析
12. 一只不透明的袋中，装有 $3$ 枚白色棋子和 $n$ 枚黑色棋子，除颜色外其余均相同 $.$ 若小明从中随机摸出一枚棋子，多次实验后发现摸到黑色棋子的频率稳定在 $80 %$ ，则 $n$ 的值可能是．

查看试题解析
13. 在Rt△ABC中，∠C=90°，AB=4，BC=3，则sinA的值是.

查看试题解析
14. 若关于 $x$ 的一元一次不等式组 $\{\begin{array}{l} x - 2 < 0 \\ x + m > 2 \end{array}$ 无解，则 $m$ 的取值范围为．

查看试题解析
15. 如图，在正方形 $A B C D$ 中，点F为 $C D$ 上一点， $B F$ 与 $A C$ 交于点E．若 $∠ C B F = 18 °$ ，则 $∠ A E D$ 等于度．

查看试题解析
16. 如图， $△ O A B$ 是等腰直角三角形，直角顶点与坐标原点重合，若点B在反比例函数 $y = \frac{1}{x} (x > 0)$ 的图象上，则经过点A的反比例函数表达式为．

查看试题解析

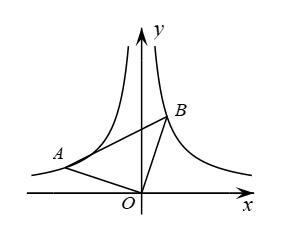
三、解答题：本题共6小题，共96分。解答应写出文字说明，证明过程或演算步骤。

17. 某校的一个社会实践小组对本校学生中开展主题为“垃圾分类知多少”的专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，划分等级后的数据整理如表：
等级
非常了解
比较了解
基本了解
不太了解
频数
$20$
$35$
$41$
$4$

(1)、请根据调查结果，若该校有学生 $600$ 人，请估计这些学生中“比较了解”垃圾分类知识的人数．

(2)、在“比较了解”的调查结果里，其中九 $(1)$ 班学生共有 $3$ 人，其中 $2$ 名男生和 $1$ 名女生，在这 $3$ 人中，打算随机选出 $2$ 位进行采访，求出所选两位同学恰好是 $1$ 名男生和 $1$ 名女生的概率． $($ 要求列表或画树状图 $)$

查看试题解析
18. 重庆是一座美丽的山坡，某中学依山而建，校门 $A$ 处，有一斜坡 $A B$ ，长度为 $13$ 米，在坡顶 $B$ 处看教学楼 $C F$ 的楼顶 $C$ 的仰角 $∠ C B F = 53 °$ ，离 $B$ 点 $4$ 米远的 $E$ 处有一花台，在 $E$ 处仰望 $C$ 的仰角 $∠ C E F = 63.4 °$ ， $C F$ 的延长线交校门处的水平面于 $D$ 点， $F D = 5$ 米． $($ 参考数据： $t a n 53 ° \approx \frac{4}{3}$ ， $t a n 63.4 ° \approx 2)$

(1)、求斜坡 $A B$ 的坡度 $i$ ．

(2)、求 $D C$ 的长．

查看试题解析
19. 某学校建立了劳动基地，计划在基地上种植甲、乙两种树苗 $.$ 已知甲种树苗的单价比乙种树苗的单价多 $10$ 元； $3$ 棵甲种树苗与 $4$ 棵乙种树苗的总价相等．

(1)、求甲、乙两种树苗的单价分别为多少元？

(2)、若购买甲、乙两种树苗共 $500$ 棵，且甲种树苗的数量不少于乙种树苗的两倍 $.$ 请为采购组设计最省钱的方案，并求出此时的总费用？

查看试题解析
20. 如图，点A，F，C，D在同一条直线上，点B，E分别在直线 $A D$ 两侧，且 $A B = D E$ ， $∠ A = ∠ D$ ， $A C = D F$ .

(1)、求证：四边形 $B C E F$ 是平行四边形；

(2)、若 $∠ A B C = 90 °$ ， $E F = 3$ ， $A B = 4$ ，当 $C D$ 为何值时，四边形 $B C E F$ 是菱形.

查看试题解析
21. 已知：如图， $A B$ 是圆 $O$ 的直径， $C D$ 是圆 $O$ 的弦， $A B ⊥ C D$ ， $E$ 为垂足， $A E = C D = 8$ ， $F$ 是 $C D$ 延长线上一点，连接 $A F$ 交圆 $O$ 于 $G$ ，连接 $A D$ 、 $D G$ ．

(1)、求圆 $O$ 的半径；

(2)、求证： $△ A D G$ ∽ $△ A F D$ ；

(3)、当点 $G$ 是弧 $A D$ 的中点时，求 $△ A D G$ 得面积与 $△ A F D$ 的面积比．

查看试题解析
22. 抛物线 $y = a x^{2} + b x + 3$ 过点 $A (- 1,0)$ ，点 $B (3,0)$ ，顶点为 $C$ ，与 $y$ 轴相交于点 $D$ ，点 $P$ 是该抛物线上一动点，设点 $P$ 的横坐标为 $m (1 < m < 3)$

(1)、求抛物线的表达式．

(2)、如图 $1$ ，连接 $B D$ ， $P B$ ， $P D$ ，若 $△ P B D$ 的面积为 $3$ ，求 $m$ 的值；

(3)、连接 $A C$ ，过点 $P$ 作 $P M ⊥ A C$ 于点 $M$ ，是否存在点 $P$ ，使得 $P M = 2 C M$ ，如果存在，请求出点 $P$ 的坐标；如果不存在，请说明理由．

查看试题解析

等级	非常了解	比较了解	基本了解	不太了解
频数	$20$	$35$	$41$	$4$

$x$	$- 2$	$- 1$	$0.5$	$1.5$
$y$	$5$	$0$	$- 3.75$	$- 3.75$