贵州省铜仁市印江土家族苗族自治县2023-2024学年八年级下学期数学期中试题

试卷更新日期：2024-05-20 类型：期中考试

进入出卷网下载

一、选择题（以下每小题均有A,B,C,D四个选项，其中只有一个选项正确，每小题3分，共36分）

1. 教育部门高度重视校园安全教育，要求各级各类学校从认识安全警告标志入手开展安全教育．下列安全图标是中心对称图形的是（）

A、注意安全 B、急救中心 C、水深危险 D、禁止攀爬

查看试题解析
2. 在平面直角坐标系中，点 $P (4, - 3)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 如图，小星利用刻度直尺（单位： $c m$ ）测量三角形纸片的尺寸，点B ， C分别对应刻度尺上的刻度2和8，D为 $B C$ 的中点，若 $∠ B A C = 90 °$ ，则 $A D$ 的长为（）

A、 $3 c m$ B、 $4 c m$ C、 $5 c m$ D、 $6 c m$

查看试题解析
4. 如图，小红想测量池塘两端A ， B的距离，他采用了如下方法：在 $A B$ 的一侧选择一点C ，连接 $A C, B C$ ，再分别找出 $A C, B C$ 的中点D ， E ，连接 $D E$ ，现测得 $D E = 10$ 米，则A ， B之间的距离为（）

A、40米 B、30米 C、20米 D、15米

查看试题解析
5. 中国结寓意团圆、美满，以独特的东方神韵体现中国人民的智慧和深厚的文化底蕴，小陶家有一个菱形中国结装饰．测得 $B D = 8 c m, A C = 6 c m$ ．则该菱形的面积为（）

A、 $24 c m^{2}$ B、 $48 c m^{2}$ C、 $10 c m^{2}$ D、 $12 c m^{2}$

查看试题解析
6. 如图，在四边形 $A B C D$ 中，对角线 $A C$ 和 $B D$ 相交于点O ，下列条件不能判断四边形 $A B C D$ 是平行四边形的是（）

A、 $A B ∥ D C, A D ∥ B C$ B、 $A B ∥ D C, A D = B C$ C、 $A B = D C, A D = B C$ D、 $O A = O C, O B = O D$

查看试题解析
7. 如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画圆弧，分别交AB、AC于点D、E，再分别以点D、E为圆心，大于 $\frac{1}{2}$ DE长为半径画圆弧，两弧交于点F，作射线AF交边BC于点G．若CG＝3，AB＝10，则△ABG的面积是（）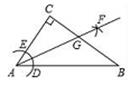

A、3 B、10 C、15 D、30

查看试题解析
8. 如图为长方形 $A B C D$ ，一条直线将该矩形分割成两个多边形，若这两个多边形的内角和分别为a和b ，则 $a + b$ 不可能是（）

A、 $360 °$ B、 $540 °$ C、 $630 °$ D、 $720 °$

查看试题解析
9. 下列命题是真命题的是（）

A、四边都相等的四边形是矩形 B、对角线互相垂直的平行四边形是正方形 C、菱形的对角线相等 D、对角线相等且互相平分的四边形是矩形

查看试题解析
10. 如图的数轴上，点A ， C对应的实数分别为1，3，线段 $A B ⊥ A C$ 于点A ，且 $A B$ 长为1个单位长度，若以点C为圆心， $B C$ 长为半径的弧交数轴于0和1之间的点P ，则点P表示的实数为（）

A、 $3 - \sqrt{10}$ B、 $3 - \sqrt{5}$ C、 $\sqrt{5}$ D、 $\sqrt{5} - 2$

查看试题解析
11. 如图．菱形 $A B C D$ 的对角线 $A C, B D$ 相交于点O ， P为 $A B$ 边上一动点（不与点A ， B重合）． $P E ⊥ O A$ 于点 $E, P F ⊥ O B$ 于点F ，若 $A B = 8, ∠ B A D = 60 °$ ，则线段 $E F$ 长度的最小值为（）

A、 $2 \sqrt{3}$ B、 $2 \sqrt{2}$ C、 $4 \sqrt{3}$ D、 $4 \sqrt{2}$

查看试题解析
12. 如图，正方形 $A B C D$ 中， $A B = 6$ ，点E在边 $C D$ 上，且 $C D = 3 D E$ ，将 $△ A D E$ 沿 $A E$ 对折至 $△ A F E$ ，延长 $E F$ 交边 $B C$ 于点G ，连接 $A G 、 C F$ ．则下列给论：① $B G = C G$ ；② $A G ∥ C F$ ；③ $S_{△ E G C} = S_{△ A F E}$ ；④ $∠ A G B + ∠ A E D = 145 °$ ．其中错误的是（）

A、① B、② C、③ D、④

查看试题解析

二、填空题（每小题4分，共16分）

13. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ A = 20 °$ ，则 $∠ B$ 的度数为．

查看试题解析
14. 如图是贵州省部分城市在地图中的位置，若贵阳的位置坐标为 $(1, 3)$ ，安顺的位置坐标为 $(0, 1)$ ，请在图中建立适当的直角坐标系，写出铜仁的位置坐标为．

查看试题解析
15. 如图，在平行四边形 $A B C D$ 中，对角线 $A C 、 B D$ 相交于点O ，在不添加任何辅助线的情况下，请你添加一个条件，使平行四边形 $A B C D$ 是菱形．

查看试题解析
16. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C = 3$ ，点D在直线 $A C$ 上， $A D = 1$ ，过点D作 $D E ∥ A B$ 交直线 $B C$ 于点E ，连接 $B D$ ，点O是线段 $B D$ 的中点，连接 $O E$ ，则 $O E$ 的长为．

查看试题解析

三、解答题（本大题共9题，共98分，解答应写出必要的文字说明、证明过程或演算步骤）

17.

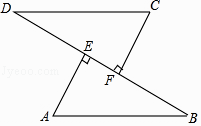
(1)、已知 $△ A B C$ 的三边a、b、c满足 $\sqrt{a - 1} + | b - \sqrt{3} | + (c - 2)^{2} = 0$ ，判断 $△ A B C$ 是否为直角三角形？

(2)、一个多边形的内角和是它的外角和的5倍，求这个多边形是几边形？

查看试题解析
18. 如图，已知AB=CD，AE⊥BD，CF⊥BD，垂足分别为E，F，BF=DE，求证：AB∥CD．

查看试题解析
19. 如图，在平行四边形 $A C F D$ 中，点B ， E分别在 $A C, D F$ 上， $A B = F E, A F$ 分别交 $B D, C E$ 于点M ， N ．

(1)、求证：四边形 $B C E D$ 是平行四边形；

(2)、已知 $D E = 6$ ，连接 $B N$ ，若 $B N$ 平分 $∠ D B C$ ，求 $C N$ 的长．

查看试题解析

20. 某实践探究小组在放风筝时想测量风筝离地面的垂直高度，通过勘测，得到如下记录表：

测量示意图
测量数据	边的长度	①测得水平距离 $B C$ 的长为15米．
		②根据手中剩余线的长度计算出风筝线 $A B$ 的长为17米．
		③小明牵线放风筝的手到地面的距离为1.7米．

数据处理组得到上面数据以后做了认真分析，他们发现根据勘测组的全部数据就可以计算出风筝离地面的垂直高度 $A D$ ．请完成以下任务．

(1)、已知：如图，在

R t △ A B C

中，

∠ A C B = 90 °, B C = 15, A B = 17

，求线段

A D

的长．

(2)、如果小明想要风筝沿

D A

方向再上升12米，

B C

长度不变，则他应该再放出多少米线？

查看试题解析

21. 已知：A（0，1），B（2，0），C（4，3）

(1)、在坐标系中描出各点，画出△ABC；

(2)、求△ABC的面积．

查看试题解析
22. 如图，线段 $A B$ 是某景区的一条最佳观赏线，四边形 $A B C D$ 是紧邻景区的一个广场，其中 $A C ⊥ B D$ 于点O ， $B C = D C = 60 m, ∠ D C B = 90 °$ ， $∠ A B C = 105 °$ ．现计划在 $A C$ 上修建一个便利店F ，为使游客从B处到便利店F购买物品后，返回到观赏线 $A B$ 上的某处路程最短．请解决下列问题：

(1)、画出符合上述条件便利店F的位置；

(2)、求出上述最短路程．

查看试题解析
23. 如图，在 $△ A B C$ 中，O是边 $A C$ 上的一个动点，过点O作直线 $M N ∥ B C$ ，交 $∠ A C B$ 的平分线于点E ，交 $△ A B C$ 的外角 $∠ A C D$ 的平分线于点F ．

(1)、求证： $O E = O F$ ；

(2)、若 $C E = 12, C F = 5$ ，求 $O C$ 的长；

(3)、连接 $A E, A F$ ，当点O在边 $A C$ 上运动到什么位置时，四边形 $A E C F$ 是矩形？请说明理由．

查看试题解析
24. 如图，将一张矩形纸片 $A B C D$ 沿着对角线 $B D$ 向上折叠，顶点C落到点E处， $B E$ 交 $A D$ 于点F ．

(1)、求证： $△ A B F ≌ △ E D F$ ；

(2)、如图，过点D作 $D G ∥ B E$ ，交 $B C$ 于点G ，连接 $F G$ 交 $B D$ 于点O ．
①判断四边形 $B F D G$ 的形状，并说明理由；
②若 $A B = 6, A D = 8$ ，求 $F G$ 的长．

查看试题解析
25. 请帮数学兴趣小组完成下列探究活动．
问题：如图①， $∠ M O N = 60 °$ ，点A在边 $O M$ 上，点P是边 $O N$ 上一动点，以线段 $A P$ 为斜边作等腰 $R t △ A C P$ （点C和点O在 $A P$ 的两侧），连接 $O C$ ，将线段 $C O$ 绕点C逆时针旋转 $90 °$ 至 $C B$ ，连接 $P B$ ．
图① 图② 备用图

(1)、如图①，小星同学得出 $△ O A C ≌ △ B P C$ ，他的判断理由是；（在①②③④中选取一个填写）
① $S S S$ ② $S A S$ ③ $A A S$ ④ $A S A$

(2)、如图②，小颖同学作 $B D ⊥ O N$ 于点D ，她探究发现 $O A$ 与 $B D$ 存在某种数量关系，请你写出 $O A$ 与 $B D$ 的数量关系并说明理由；

(3)、小红同学认为：根据小颖的结果，连接 $O B$ ，当 $O A = 2$ ，且 $△ A O P$ 是直角三角形时，能求出 $O B^{2}$ 的值．请你帮她求出 $O B^{2}$ 的值．

查看试题解析