河北省保定市定州市2023-2024学年八年级下学期数学期中试题

试卷更新日期：2024-05-20 类型：期中考试

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分）

1. 化简 $\sqrt{(- 2)^{2}}$ 的结果是（）

A、 $- 2$ B、2 C、 $\pm 2$ D、4

查看试题解析
2. 下列二と根式中，最简二次根式是（）

A、 $\sqrt{9}$ B、 $\sqrt{12}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{10}$

查看试题解析
3. 下列计算结果正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $2 \sqrt{3} - \sqrt{3} = 2$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\frac{\sqrt{2}}{\sqrt{5}} = 5 \sqrt{10}$

查看试题解析
4. 要做一个直角三角形的木架，以下四组木棒中，哪一组的三条能够刚好做成？（）

A、2，3，4 B、3，4，5 C、4，5，6 D、1，1，2

查看试题解析
5. 如图，在高为 $5m$ ，坡面长为 $13m$ 的楼梯表面铺地毯，地毯的长度至少需要（）

A、 $17m$ B、 $18m$ C、 $25m$ D、 $26m$

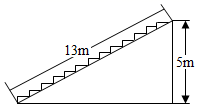查看试题解析
6. 在▱ABCD中，∠A：∠B：∠C：∠D的值可以是（）

A、1：2：3：4 B、1：2：2：1 C、1：1：2：2 D、2：1：2：1

查看试题解析
7. 如图，在平行四边形 $A B C D$ 中， $A E ⊥ C D$ 于点 $E$ ， $∠ B = 65 °$ ，则 $∠ D A E$ 等于（）

A、 $15 °$ B、 $25 °$ C、 $35 °$ D、 $65 °$

查看试题解析
8. 如图，顺次连接四边形ABCD各边中点得四边形EFGH ，要使四边形EFGH为矩形，应添加的条件是（）

A、AB $//$ DC B、AC＝BD C、AC⊥BD D、AB＝DC

查看试题解析
9. 平行四边形 $A B C D$ 的对角线AC ， BD的交点 $O$ 在坐标原点．且AD平行于 $x$ 轴．若点 $A$ 坐标为 $(- 1, 2)$ ，则点 $C$ 的坐标为（）

A、 $(1, - 2)$ B、 $(2, - 1)$ C、 $(1, - 3)$ D、 $(2, - 3)$

查看试题解析
10. 如图，有一个绳索拉直的木马秋千，绳索AB的长度为5米.若将它往水平方向向前推进3米（即DE=3米），且绳索保持拉直的状态，则此时木马上升的高度为（）

A、1米 B、 $\sqrt{2}$ 米 C、2米 D、4米

查看试题解析
11. 对角线长分别为6和8的菱形 $A B C D$ 如图所示，点O为对角线的交点，过点O折叠菱形，MN是折痕点B的对应点是 $B^{'}$ ，若 $B^{'} M = 1$ ，则CN的长为（）

A、7 B、6 C、5 D、4

查看试题解析
12. 如图，延长矩形 $A B C D$ 的边 $B C$ 至点E，使 $C E = B D$ ，连接 $A E$ ，如果 $∠ A B D = 60 °$ ，那么 $∠ B A E$ 的度数是（）

A、 $40 °$ B、 $55 °$ C、 $75 °$ D、 $80 °$

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

13. 若代数式 $\sqrt{3 x - 1}$ 在实数范围内有意义．则 $x$ 的取值范围是．

查看试题解析
14. 如图，在 $△ A B C$ 中，D、E分别为AB和AC中点，若 $B C = 12$ ，则DE的长为．

查看试题解析
15. 如图，矩形 $A B C D$ 中， $A B = 3$ ，两条对角线AC、BD所夹的钝角为120°，则BC的长为．

查看试题解析
16. 计算：若 $a = 3 - \sqrt{10}$ ，则代数式 $a^{2} - 6 a - 2 =$ ．

查看试题解析
17. 如图，在平面直角坐标系中，四边形 $O A B C$ 是菱形．若点A的坐标是 $(8, 15)$ ．则菱形的周长为．

查看试题解析
18. 如图，在 $△ A B C$ 中， $A B = 6, A C = 8, B C = 10$ ， $P$ 为边BC上一动点（且点P不与点B、C重合）， $P E ⊥ A B$ 于 $E$ ， $P F ⊥ A C$ 于 $F$ ．则EF的最小值为．

查看试题解析

三、解答题（本大题共7小题，共66分）

19. 计算：

(1)、 $2 \sqrt{27} + \sqrt{12}$

(2)、 $4 \sqrt{\frac{1}{2}} \times \sqrt{48} - \sqrt{54} + \sqrt{6}$

查看试题解析
20. 《九章算术》中记载“今有竹高一丈八，末折抵地，去本6尺．问：折者高几何？”译文：一根竹子，原高一丈八尺，虫伤有病，一阵风将竹子折断，其顶端恰好着地，着地处离竹子根部6尺远，问：折断处离地还有多高的竹子？（1丈=10尺）

查看试题解析
21. 已知点E、F为 $▱ A B C D$ 对角线AC上的两点， $A E = C F$ ．
求证：四边形 $B F D E$ 是平行四边形．

查看试题解析
22. 已知：如图，在四边形 $A B C D$ 中， $A B = D C$ ， $A D = B C$ ，点E、F分别在边BC、AD上， $A F = C E$ ， EF与对角线BD交于点O ．求证：O是BD的中点．

查看试题解析
23. 如图，在菱形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 交于点 $O$ ，过点 $C$ 作 $B D$ 的平行线，过点 $D$ 作 $A C$ 的平行线，两直线相交于点 $E$ .

(1)、求证：四边形 $O C E D$ 是矩形；

(2)、若 $C E = 1$ ， $D E = 2$ ，求菱形 $A B C D$ 的面积.

查看试题解析
24. 如图，在正方形 $A B C D$ 中，点E在BC的延长线上，AE分别交DC ， BD于F ， G ，点H为EF的中点．

(1)、若 $∠ D A G = 20 °$ ，求 $∠ D C C$ 的度数；

(2)、求证： $G C ⊥ C H$ ．

查看试题解析
25. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ． BD平分 $∠ A B C$ 交AC于点D ．过D作 $D E / / B C$ 交AB于点E ． $D F / / A B$ 交BC于点F ．连接EF ．

(1)、求证：四边形 $B F D E$ 是菱形；

(2)、若 $A B = 8$ ， $A D = 4$ ，求BF的长．

查看试题解析