广东省中山市共进联盟2023-2024学年八年级下学期数学期中试卷

试卷更新日期：2024-05-20 类型：期中考试

进入出卷网下载

一、选择题(共10小题，每小题3分，满分30分)

1. 下列式子中是最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{4}$ C、 $\sqrt{5}$ D、 $\sqrt{12}$

查看试题解析
2. 下列运算结果正确的是( )

A、 $\sqrt{{(- 4)}^{2}} = 2$ B、 ${(\sqrt{2})}^{2} = 4$ C、 $\sqrt{2} \times \sqrt{5} = \sqrt{10}$ D、 $\sqrt{6} \div \sqrt{2} = 3$

查看试题解析
3. 如果下列各组数是三角形的三边长，那么能组成直角三角形的一组数是( )

A、2，3，4 B、3，4，6 C、4，6，7 D、5，12，13

查看试题解析
4. 下列二次根式中，与 $\sqrt{2}$ 是同类二次根式的是( )

A、 $\sqrt{8}$ B、 $\sqrt{6}$ C、 $. \sqrt{4}$ D、 $\sqrt{12}$

查看试题解析
5. 矩形具有而菱形不具有的性质是( )

A、对角线互相平分 B、对角线互相垂直 C、四个角相等 D、四条边相等

查看试题解析
6. 如图，在△ABC中，AB＝8，∠C＝90°，∠A＝30°，DE是中位线，则DE的长为（）

A、2 B、3 C、4 D、2 $\sqrt{3}$

查看试题解析
7. 如图，在平行四边形ABCD中，AE垂直于CD，E是垂足.如果∠B=55°，那么∠DAE的角度为( )

A、25° B、35° C、45° D、55°

查看试题解析
8. 如图，在矩形ABCD中，两条对角线AC、BD相交于点O，若OB=5.则AC=( )

A、10 B、8 C、 $5 \sqrt{3}$ D、5

查看试题解析
9. 如图，平面直角坐标系xOy中，点A，B的坐标分别是(﹣2，0)和(0，3)，以A为圆心，AB长为半径画弧，交x轴的正半轴于点C，则点C的横坐标是( )

A、 $- \sqrt{13}$ B、 $\sqrt{13}$ C、 $- 2 - \sqrt{13}$ D、 $- 2 + \sqrt{13}$

查看试题解析
10. 如图，在平面直角坐标系中，正方形ABCD的顶点D在y轴上，A(-3，0)，B(1，b)，则正方形ABCD的面积为( )

A、34 B、25 C、20 D、16

查看试题解析

二、填空题(共5小题，每小题4分，满分20分)

11. 要使代数式 $\sqrt{x - 2}$ 有意义，则x的取值范围是

查看试题解析
12. 计算 $\frac{6}{\sqrt{3}}$ 的结果是.

查看试题解析
13. 如图，菱形ABCD的顶点B在x轴上，顶点C在y轴上，点A的坐标为(-4，1)，点C的坐标为(0，1)，则点D的坐标为.

查看试题解析
14. 菱形的边长为10，一条对角线为16，它的面积是.

查看试题解析
15. 如图，四边形ABCD与CEFG均为矩形，使得G，D，C共线，B，C，E共线，取AD中点M，连接AF，GM交于点H，若BC=EF=4，CD=CE=2，则AH=.

查看试题解析

三、解答题(一)(共4小题，每小题6分，共24分)

16. 计算： $\sqrt{48} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{10} + \sqrt{20} .$

查看试题解析
17. 已知 $x = \sqrt{3} + 1 ， y = \sqrt{3} - 1 ，$ 求代数式 $x^{2} y + x y^{2}$ 的值.

查看试题解析
18. 如图，图1是某品牌婴儿车，图2为其简化结构示意图.根据安全标准需满足BC⊥CD，现测得AB=CD=6dm，BC=3dm，AD=9dm，其中AB与BD之间由一个固定为90°的零件连接(即∠ABD=90°)，通过计算说明该车是否符合安全标准.

查看试题解析
19. 如图，已知，AB⊥BD，CD⊥BD，AD=BC，求证：四边形ABCD是平行四边形.

查看试题解析

四、解答题(二)(共3小题，每小题8分，共24分)

20. 如图，正方形网格中的每个小正方形边长都为1.

(1)、分别求出线段AB、AC、BC的长.

(2)、判断△ABC的形状，并说明你的理由.

查看试题解析
21. 如图，在四边形ABCD中， AD∥BC，∠D=90°，E为边BC上一点，且EC=AD，连接AC.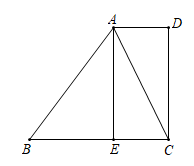

(1)、求证：四边形AECD是矩形；

(2)、若AC平分∠DAB，AB=5，EC=2，求AE的长，

查看试题解析
22. 如图，在平行四边形ABCD中，AD>AB，AE平分∠BAD，交BC于点E，过点E作EF∥AB交AD于点F.

(1)、求证：四边形ABEF是菱形；

(2)、若菱形ABEF的周长为16，∠EBA=120°，求AE的大小.

查看试题解析

五、解答题(三)(共2小题，第23题10分，第24题12分，共22分)

23. 如图，已知四边形ABCD是正方形，点E、F分别在AD、DC上，BE与AF相交于点G，且BE=AF.

(1)、求证：BE⊥AF；

(2)、如果正方形ABCD的边长为5，AE=2，点H为BF的中点，连接GH.求GH的长.

查看试题解析
24. 定义：有两个相邻的内角是直角，并且有两条邻边相等的四边形称为邻等四边形.邻等四边形中，相等两邻边的夹角称为邻等角.

(1)、如图1，在四边形ABCD中，∠BAD=∠B=90°，对角线AC平分∠BCD，求证：四边形ABCD是邻等四边形；

(2)、如图2，在5×6的方格纸中，A，B，C三点均在格点上，若四边形ABCD是邻等四边形，请画出所有符合条件的格点D，并分别用D₁ ， D₂ ， D₃ ， …表示；

(3)、如图3，四边形ABCD是邻等四边形，∠A=∠B=90°，∠BCD为邻等角.若AB=8，AD=6，求邻等四边形ABCD的周长.

查看试题解析