2025艺考生专用高考数学一轮复习之函数的概念与性质
试卷更新日期:2024-05-16 类型:一轮复习
一、选择题
-
1. 已知函数 ,则 ( )A、0 B、1 C、2 D、42. 若函数在其定义域内是一个单调递增函数,则实数的取值范围是( )A、 B、 C、 D、3. 已知函数在上不单调,则的取值范围为( )A、 B、 C、 D、4. 已知对任意实数 , 有 , , 且时,导函数分别满足 , , 则时,成立的是( )A、 B、 C、 D、5. 设函数在区间上的最大值和最小值分别为M , m则( )A、4 B、6 C、10 D、246. 定义在上的函数满足:对于定义域上的任意 , , 当时,恒有 , 则称函数为“理想函数”.给出下列四个函数:
①;②;③;④能被称为“理想函数”的有( )
A、0个 B、1个 C、2个 D、3个7. 函数的图象大致为( )A、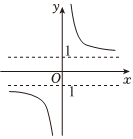 B、
B、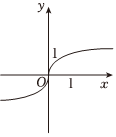
C、 D、
D、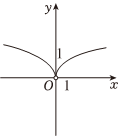 8. 函数的零点所在的区间是( )A、 B、 C、 D、
8. 函数的零点所在的区间是( )A、 B、 C、 D、二、多项选择题
-
9. 下列各组函数中,两个函数是同一函数的有( ).A、与 B、与 C、与 D、与10. 下列命题中正确的有( )A、幂函数,且在单调递减,则 B、的单调递增区间是 C、定义域为 , 则 D、的值域是11. 下列命题为真命题的有( )A、函数的单调递减区间为 B、函数的图象关于点对称 C、函数与函数是同一个函数 D、函数的最小值为-1
三、填空题
-
12. 函数的导函数为 , 满足关系式 , 则的值为.13. 设函数在区间上的最大值为M,最小值为N,则 的值为.14. 函数 的定义域为.
四、解答题