2024年北师大版数学七年级第二学期期末模拟试卷一

试卷更新日期：2024-05-16 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 计算（a²）³ ，正确结果是（　　）

A、a⁵ B、a⁶ C、a⁸ D、a⁹

查看试题解析
2. 下列图案中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 $m^{2} \cdot m^{3} = m^{6}$ B、 $- (m - n) = - m + n$ C、 $m (m + n) = m^{2} + n$ D、 $(m + n)^{2} = m^{2} + n^{2}$

查看试题解析
4. “五一”假期，宜昌旅游市场接待游客 $606.7$ 万人次，实现旅游总收入 $41.5$ 亿元．数据“ $41.5$ 亿”用科学记数法表示为（）．

A、 $415 \times 1 0^{7}$ B、 $41.5 \times 1 0^{8}$ C、 $4.15 \times 1 0^{9}$ D、 $4.15 \times 1 0^{10}$

查看试题解析
5. 下列长度的三条线段能首尾相接构成三角形的是（）

A、 $1 c m$ ， $2 c m$ ， $3 c m$ B、 $3 c m$ ， $4 c m$ ， $5 c m$ C、 $4 c m$ ， $5 c m$ ， $10 c m$ D、 $6 c m$ ， $9 c m$ ， $2 c m$

查看试题解析
6. 如图，一块直角三角板的直角顶点放在直尺的一边上．如果 $∠ 1 = 70 °$ ，那么 $∠ 2$ 的度数是（　　）

A、 $20 °$ B、 $25 °$ C、 $30 °$ D、 $45 °$

查看试题解析
7. 如图，若△ABC≌△ADE，则下列结论中一定成立的是（）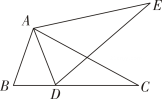

A、AC＝DE B、∠BAD＝∠CAE C、AB＝AE D、∠ABC＝∠AED

查看试题解析
8. 如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成右边的矩形．根据图形的变化过程写出的一个正确的等式是（）

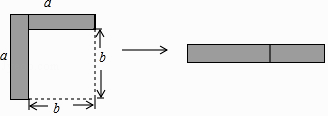A、（a﹣b）²=a²﹣2ab+b² B、a（a﹣b）=a²﹣ab C、（a﹣b）²=a²﹣b² D、a²﹣b²=（a+b）（a﹣b）

查看试题解析
9. 下列事件中是不可能事件的是（）

A、守株待兔 B、瓮中捉鳖 C、水中捞月 D、百步穿杨

查看试题解析
10. 如图， $△ A B C$ 中，若 $∠ B A C = 80 °$ ， $∠ A C B = 70 °$ ，根据图中尺规作图的痕迹推断，以下结论错误的是（）

A、 $∠ B A Q = 40 °$ B、 $D E = \frac{1}{2} B D$ C、 $A F = A C$ D、 $∠ E Q F = 25 °$

查看试题解析

二、填空题（每题3分，共18分）

11. 若m+n=10，mn=5，则 $m^{2} + n^{2}$ 的值为．

查看试题解析
12. 如图，点B、F、C、E在一条直线上，AB∥ED，AC∥FD，要使△ABC≌△DEF，还需添加一个条件是．（只需添一个）

查看试题解析
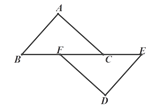13. 等腰三角形的周长是 $13 c m$ ，其中一边长是 $5 c m$ ，则该等腰三角形的腰长为．

查看试题解析
14. 如图，将一条长方形纸片沿 $A B$ 折叠，已知 $∠ D A B = 70^{\circ}$ ，则 $∠ C B F =$

查看试题解析
15. 如图，在△ABC中，AD是BC边上的高，AE是∠BAC的平分线，若∠B=70°，∠C=40°，则∠DAE的度数为．

查看试题解析

16. 王勇买了一张

30

元的租书卡，每租一本书后卡中剩余金额

y

（元）与租书本数

x

（本）之间的关系式为.

租书数 $/$ 本	卡中余额 $/$ 元
$1$	$30 - 0.8$
$2$	$30 - 1.6$
$3$	$30 - 2.4$
……	……

查看试题解析

三、解答题（共9题，共72分）

17. 计算： $(a b^{2})^{2} \cdot (- a^{3} b)^{3} \div (- 3 a^{2} b^{3})$

查看试题解析
18. 计算： ${(－ 1)}^{2018} + {(－ \frac{1}{3})}^{－ 2} － {(\frac{99}{100})}^{0} + 16 \times 2^{－ 3}$

查看试题解析
19. 先化简，再求值： $2 x (2 + y) + (x + y) (x - y) - {(x + y)}^{2}$ ，其中 $x = 2$ ， $y = - 1$ ．

查看试题解析
20.

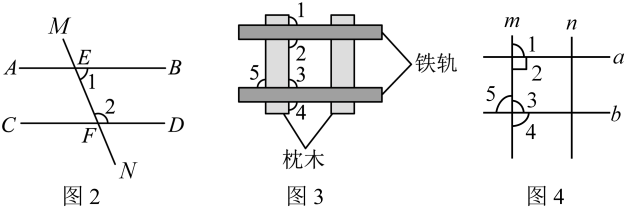(1)、我们曾用移动三角尺的方法画出了两条平行线（如图1），请说明依据的基本事实为：；

(2)、基本事实可作为依据，用来证明新的结论．请根据以上基本事实证明平行线的判定方法：“同旁内角互补，两直线平行”
已知：如图2，∠1和∠2是直线 $A B 、 C D$ 被直线 $E F$ 截出的同旁内角，且 $∠ 1$ 与 $∠ 2$ 互补，求证： $A B ∥ C D$ ．（推理过程请注明理由）

(3)、平行线的判定在实际生活中有许多应用：如图3，在铺设铁轨时，两条铁轨必须是互相平行的．将铁轨和枕木看成直线（如图4 所示，直线a、b为直轨，m、n为枕木）， $∠ 2$ 是直角，可以通过度量图中已标出的哪个角的度数，来判断两条铁轨是否平行？为什么？

查看试题解析
21. 如图，在3×3的正方形网格中，有格点△ABC和△DEF，且△ABC和△DEF关于某条直线成轴对称，请在下面给出的图中，画出3个不同位置的△DEF及其对称轴MN．

查看试题解析
22. 如图，有一个可以自由转动的均匀转盘，转盘被平均分成 $6$ 等份，每个扇形区域内分别标有 $3$ ， $4$ ， $5$ ， $6$ ， $7$ ， $8$ 这六个数字，转动转盘，当转盘停止转动后，指针指向的数字即为转出的数字，请回答下列问题：

(1)、随机转动转盘，转出数字 $2$ 是事件，转出数字 $7$ 是事件；（从“随机”，“必然”，“不可能”中选一个，填空）

(2)、随机转动转盘，转出的数字大于 $5$ 的概率是；

(3)、现有两张分别写有 $4$ 和 $5$ 的卡片，随机转动转盘，转盘停止转动后，将转出的数字与两张卡片上的数字分别作为三条线段的长度．求这三条线段能构成等腰三角形的概率．

查看试题解析
23. 小明家、新华书店、学校在一条笔直的公路旁，某天小明骑车上学，当他骑了一段后，想起要买某本书，于是又返回到刚经过的新华书店，买到书后继续骑车去学校，他本次骑车上学的过程中离家距离与所用的时间的关系如图所示，请根据图象提供的信息回答下列问题：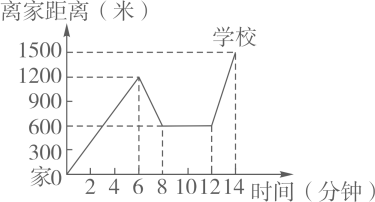

(1)、小明家到学校的距离是米；小明在书店停留了分钟；

(2)、如果骑车的速度超过了300米/分就超越了安全限度，小明买到书后继续骑车到学校的这段时间的骑车速度在安全限度内吗？请说明理由；

(3)、请直接写出小明出发后多长时间离家的距离为900米？

查看试题解析
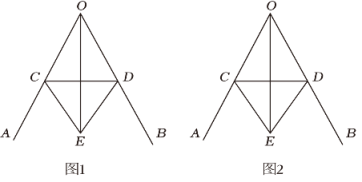
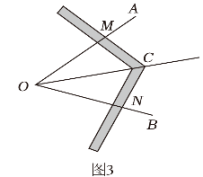24. 综合与实践：

(1)、问题探究：如图1是古希腊数学家欧几里得所着的《几何原本》第1卷命题9“平分一个已知角，”即：作一个已知角的平分线，如图2是欧几里得在《几何原本》中给出的角平分线作图法：在OA和OB上分别取点C和D ，使得OC＝OD ，连接CD ，以CD为边作等边三角形CDE ，则OE就是∠AOB的平分线．请写出OE平分∠AOB的依据：；

(2)、类比迁移：小明根据以上信息研究发现：△CDE不一定必须是等边三角形，只需CE＝DE即可，他查阅资料；我国古代已经用角尺平分任意角，做法如下：如图3，在∠AOB的边OA ， OB上分别取OM＝ON ，移动角尺，使角尺两边相同刻度分别与点M ， N重合，则过角尺顶点C的射线OC是∠AOB的平分线，请说明此做法的理由；

查看试题解析
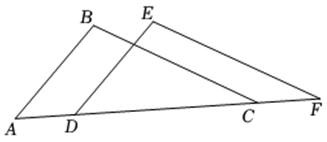25. 如图，点 $A$ ， $D$ ， $C$ ， $F$ 在同一条直线上， $AB = DE$ ， $BC = EF .$ 有下列三个条件： $① AC = DF$ ， $② ∠ ABC = ∠ DEF$ ， $③ ∠ ACB = ∠ DFE$ ．

(1)、请在上述三个条件中选取一个条件，使得 $△ ABC$ ≌ $△ DEF$ ．
你选取的条件为 ( 填写序号 ) ( 只需选一个条件，多选不得分 )，你判定 $△ ABC$ ≌ $△ DEF$ 的依据是 (填“ $SSS$ ”或“ $SAS$ ”或“ $ASA$ ”或“ $AAS$ ”)；

(2)、利用 $(1)$ 的结论 $△ ABC$ ≌ $△ DEF .$ 求证： $AB / / DE$ ．

查看试题解析