(通用版)2024年中考数学重点知识冲刺训练---二次函数
试卷更新日期:2024-05-16 类型:三轮冲刺
一、选择题
-
1. 将二次函数的图象向右平移1个单位长度,再向下平移3个单位长度,所得图象的解析式为( )A、 B、 C、 D、2. 二次函数的图象如图所示,下列四个选项中,正确的是( )
 A、 , B、 , C、 , D、 ,3. 若二次函数的部分图象如图所示,则关于的方程的解为( )
A、 , B、 , C、 , D、 ,3. 若二次函数的部分图象如图所示,则关于的方程的解为( ) A、 , B、 , C、 , D、 ,4. 二次函数的图象所示,则一次函数的图象一定不经过( )
A、 , B、 , C、 , D、 ,4. 二次函数的图象所示,则一次函数的图象一定不经过( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 抛物线y=x2-2的顶点坐标是( )A、(-2,0) B、(2,0) C、(0,2) D、(0,-2)6. 如图,二次函数的图象与轴相交于两点,则A,B两点之间的距离为( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 抛物线y=x2-2的顶点坐标是( )A、(-2,0) B、(2,0) C、(0,2) D、(0,-2)6. 如图,二次函数的图象与轴相交于两点,则A,B两点之间的距离为( ) A、3 B、4 C、5 D、67. 抛物线y=-x2+4x-4与坐标轴的交点个数是( )A、0 B、1 C、2 D、38. 经过两点的抛物线(为自变量)与轴有交点,则线段长为( )A、10 B、12 C、13 D、159. 已知二次函数y=x2+ax+b(a,b为常数).命题①:该函数的图象经过点(1,0);命题②:该函数的图象经过点(3,0);命题③:该函数的图象与x轴的交点位于y轴的两侧;命题④;该函数的图象的对称轴为直线x=1.如果这四个命题中只有一个命题是假命题,则这个假命题是( )A、命题① B、命题② C、命题③ D、命题④10. 抛物线与轴的一个交点为 , 与轴交于点 , 点是抛物线的顶点,对称轴为直线 , 其部分图象如图所示,则以下个结论:; , 是抛物线上的两个点,若 , 且 , 则;在轴上有一动点 , 当的值最小时,则点的坐标为;若关于的方程无实数根,则的取值范围是其中正确的结论有( )
A、3 B、4 C、5 D、67. 抛物线y=-x2+4x-4与坐标轴的交点个数是( )A、0 B、1 C、2 D、38. 经过两点的抛物线(为自变量)与轴有交点,则线段长为( )A、10 B、12 C、13 D、159. 已知二次函数y=x2+ax+b(a,b为常数).命题①:该函数的图象经过点(1,0);命题②:该函数的图象经过点(3,0);命题③:该函数的图象与x轴的交点位于y轴的两侧;命题④;该函数的图象的对称轴为直线x=1.如果这四个命题中只有一个命题是假命题,则这个假命题是( )A、命题① B、命题② C、命题③ D、命题④10. 抛物线与轴的一个交点为 , 与轴交于点 , 点是抛物线的顶点,对称轴为直线 , 其部分图象如图所示,则以下个结论:; , 是抛物线上的两个点,若 , 且 , 则;在轴上有一动点 , 当的值最小时,则点的坐标为;若关于的方程无实数根,则的取值范围是其中正确的结论有( )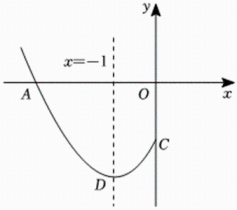 A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个二、填空题
-
11. 抛物线y=3(x﹣2)2+5的顶点坐标是 .12. 已知二次函数 , 若点在该函数的图象上,且 , 则的值为.13. 实心球是一项力量性和动作速度项目.同学小丁在某次投掷实心球所经过的路线是如图所示抛物线的一部分,已知实心球出手处距离地面的高度是1.68米,当实心球运行的水平距离为2米时,达到最大高度2米的处,则小丁此次投掷的成绩是米.
 14. 已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有 .
14. 已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有 .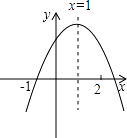
三、解答题
-
15. 已知二次函数图象过点A(2,1),B(4,1)且最大值为2,求二次函数的解析式.16. 2022年冬季奥运会和冬季残奥会两项赛事在我国首都北京和河北省石家庄市举行.某商家购进了一批冬季残奥会吉祥物“雪容融”纪念品,发现进价为40元/件的纪念品每月的销售量y(件)与售价x(元/件)的相关信息如下:
售价x(元)
50
60
70
80
…
销售量y(件)
300
280
260
240
…
(1)、求y与x的一次函数解析式;(2)、若获利不得高于进价的50%,那么售价定为多少元/件时,月销售利润达到最大?最大利润是多少元?17. 图①是古代的一种远程投石机,其投出去的石块运动轨迹是抛物线的一部分.据《范蠡兵法》记载:“飞石重十二斤,为机发,行二百步”,其原理蕴含了物理中的“杠杆原理”.在如图②所示的平面直角坐标系中,将投石机置于斜坡的底部点O处,石块从投石机竖直方向上的点C处被投出,已知石块运动轨迹所在抛物线的顶点坐标是 , . (1)、求抛物线的表达式;(2)、在斜坡上的点A建有垂直于水平线的城墙 , 且 , , , 点D , A , B在一条直线上.通过计算说明石块能否飞越城墙 .18. 直线称作抛物线的关联直线.根据定义回答以下问题:(1)、求证:抛物线与其关联直线一定有公共点;(2)、当时,求抛物线与其关联直线一定都经过的点的坐标(用字母表示).19. 如图,在平面直角坐标系中,二次函数的图像与轴交于 , 两点,点的坐标为 , 与轴交于点 , 点为抛物线的顶点
(1)、求抛物线的表达式;(2)、在斜坡上的点A建有垂直于水平线的城墙 , 且 , , , 点D , A , B在一条直线上.通过计算说明石块能否飞越城墙 .18. 直线称作抛物线的关联直线.根据定义回答以下问题:(1)、求证:抛物线与其关联直线一定有公共点;(2)、当时,求抛物线与其关联直线一定都经过的点的坐标(用字母表示).19. 如图,在平面直角坐标系中,二次函数的图像与轴交于 , 两点,点的坐标为 , 与轴交于点 , 点为抛物线的顶点 (1)、求这个二次函数的解析式;(2)、求的面积20. 定义:在平面直角坐标系中,若在函数图象W上存在一点M,绕原点顺时针旋转后的对应点N(点N与M不重合)仍在此函数图象W上,则称这个函数为“凡尔赛函数”,其中点M称为这个函数的“凡尔赛点”(1)、函数① , ② , ③ , 其中是“凡尔赛函数”的是;(填序号)(2)、若一次函数是“凡尔赛函数”,点(m为整数)是这个函数的“凡尔赛点”,求k的值;(3)、若点是二次函数(其中a,b,c为常数,)的“凡尔赛点”,点B为A的“后凡尔赛点”,由点A、B、C、D四点构成的四边形面积记为S,求S的取值范围.
(1)、求这个二次函数的解析式;(2)、求的面积20. 定义:在平面直角坐标系中,若在函数图象W上存在一点M,绕原点顺时针旋转后的对应点N(点N与M不重合)仍在此函数图象W上,则称这个函数为“凡尔赛函数”,其中点M称为这个函数的“凡尔赛点”(1)、函数① , ② , ③ , 其中是“凡尔赛函数”的是;(填序号)(2)、若一次函数是“凡尔赛函数”,点(m为整数)是这个函数的“凡尔赛点”,求k的值;(3)、若点是二次函数(其中a,b,c为常数,)的“凡尔赛点”,点B为A的“后凡尔赛点”,由点A、B、C、D四点构成的四边形面积记为S,求S的取值范围.四、综合题
-
21. 已知:抛物线y=﹣x2+bx+c经过点B(﹣1,0)和点C(2,3).(1)、求此抛物线的表达式;(2)、如果此抛物线沿y轴平移一次后过点(﹣2,1),试确定这次平移的方向和距离.22. 在平面直角坐标系中,设二次函数(a , b是常数,a≠0).(1)、判断该函数图象与x轴的交点个数,并说明理由;(2)、若该函数图象的对称轴为直线x=2,A( , m),B( , m)为该函数图象上的任意两点,其中 , 求当 , 为何值时,;(3)、若该函数图象的顶点在第二象限,且过点(1,2),当时求的取值范围.23. 在平面直角坐标系中,已知抛物线与x轴交于点两点,与y轴交于点 , 点P是抛物线上的一个动点.
 (1)、求抛物线的表达式;(2)、当点P在直线上方的抛物线上时,连接交于点D.如图1.当的值最大时,求点P的坐标及的最大值;(3)、过点P作x轴的垂线交直线于点M,连接 , 将沿直线翻折,当点M的对应点恰好落在y轴上时,请直接写出此时点M的坐标.
(1)、求抛物线的表达式;(2)、当点P在直线上方的抛物线上时,连接交于点D.如图1.当的值最大时,求点P的坐标及的最大值;(3)、过点P作x轴的垂线交直线于点M,连接 , 将沿直线翻折,当点M的对应点恰好落在y轴上时,请直接写出此时点M的坐标.