(通用版)2024年中考数学重点知识冲刺训练---函数基础知识、一次函数
试卷更新日期:2024-05-16 类型:三轮冲刺
一、选择题
-
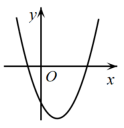
1. 根据如图所示的二次函数的图象,判断反比例函数与一次函数的图象大致是( )
 A、
A、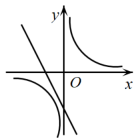 B、
B、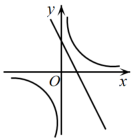 C、
C、 D、
D、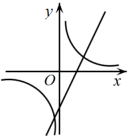 2. 已知一次函数 的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )A、 B、 C、 D、3. 下图是甲乙丙三位同学在一次长跑练习中所用时间与路程之间的函数图象,其中最先到达终点和平均速度最快的分别是( )
2. 已知一次函数 的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )A、 B、 C、 D、3. 下图是甲乙丙三位同学在一次长跑练习中所用时间与路程之间的函数图象,其中最先到达终点和平均速度最快的分别是( ) A、甲和乙 B、甲和丙 C、丙和甲 D、丙和乙4. 某烤鸭店在确定烤鸭的烤制时间时,主要依据的是表中的数据:
A、甲和乙 B、甲和丙 C、丙和甲 D、丙和乙4. 某烤鸭店在确定烤鸭的烤制时间时,主要依据的是表中的数据:鸭的质量/千克
0.5
1
1.5
2
2.5
3
3.5
4
烤制时间/分钟
40
60
80
100
120
140
160
180
设鸭的质量为x千克,烤制时间为t . 估计当x=3.8千克时,t的值约为( )
A、140 B、160 C、170 D、1805. 下面的三个问题中都有两个变量:①汽车从A地匀速行驶到B地,汽车的剩余路程y与行驶时间x;②将水箱中的水匀速放出,直至放完,水箱中的剩余水量y与放水时间x;③用长度一定的绳子围成一个矩形,矩形的面积y与一边长x,其中,变量y与变量x之间的函数关系可以利用如图所示的图象表示的是( )
 A、①② B、①③ C、②③ D、①②③6. 小聪某次从家出发去公园游玩的行程如图所示,他离家的路程为s米,所经过的时间为t分钟,下列选项中的图象,能近似刻画s与t之间关系的是( )
A、①② B、①③ C、②③ D、①②③6. 小聪某次从家出发去公园游玩的行程如图所示,他离家的路程为s米,所经过的时间为t分钟,下列选项中的图象,能近似刻画s与t之间关系的是( )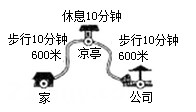 A、
A、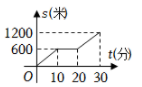 B、
B、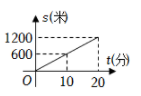 C、
C、 D、
D、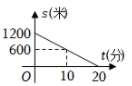 7. 如图,在平面直角坐标系中,直线 与直线 相交于点A,则关于x,y的二元一次方程组 的解是( )
7. 如图,在平面直角坐标系中,直线 与直线 相交于点A,则关于x,y的二元一次方程组 的解是( )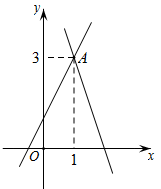 A、 B、 C、 D、8. 如图,在直角坐标系中,直线与坐标轴交于、两点,与双曲线交于点 , 过点作轴,垂足为 , 且 , 则以下结论:
A、 B、 C、 D、8. 如图,在直角坐标系中,直线与坐标轴交于、两点,与双曲线交于点 , 过点作轴,垂足为 , 且 , 则以下结论:
;
当时,;
如图,当时,;
当时,随的增大而增大,随的增大而减小.
其中正确结论的个数是 A、 B、 C、 D、9. 如图,在平面直角坐标系中,直线分别与轴、轴交于点、 , 在中从左向右依次作正方形、、 , 点、、在轴上,点在轴上,点、、在直线上;再将每个正方形分割成四个全等的直角三角形和一个小正方形,其中每个小正方形的边都与坐标轴平行,从左至右的小正方形阴影部分的面积分别记为、、 , 则可表示为
A、 B、 C、 D、9. 如图,在平面直角坐标系中,直线分别与轴、轴交于点、 , 在中从左向右依次作正方形、、 , 点、、在轴上,点在轴上,点、、在直线上;再将每个正方形分割成四个全等的直角三角形和一个小正方形,其中每个小正方形的边都与坐标轴平行,从左至右的小正方形阴影部分的面积分别记为、、 , 则可表示为 A、 B、 C、 D、10. 如图1,正方形的边长为4,为边的中点.动点从点出发沿匀速运动,运动到点时停止.设点的运动路程为 , 线段的长为 , 与的函数图象如图2所示,则点的坐标为( )
A、 B、 C、 D、10. 如图1,正方形的边长为4,为边的中点.动点从点出发沿匀速运动,运动到点时停止.设点的运动路程为 , 线段的长为 , 与的函数图象如图2所示,则点的坐标为( )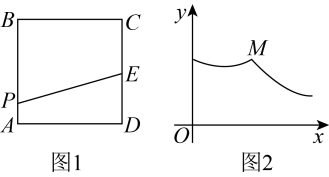 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 函数y=的自变量x的取值范围是 .
12. 已知一次函数y=2x﹣1的图象经过A(x1 , 1),B(x2 , 3)两点,则x1x2(填“>”“<”或“=”).13. 一个装有进水管和出水管的容器,开始时,先打开进水管注水,3分钟时,再打开出水管排水,8分钟时,关闭进水管,直至容器中的水全部排完.在整个过程中,容器中的水量y(升)与时间x(分钟)之间的函数关系如图所示,则图中a的值为.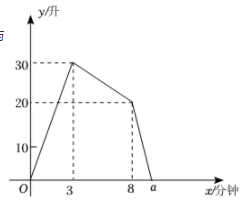 14. 已知一次函数与是常数,的图象的交点坐标是 , 不等式解集是.
14. 已知一次函数与是常数,的图象的交点坐标是 , 不等式解集是.三、解答题
-
15. 如图,在平面直角坐标系xOy中,过点的直线与直线相交于点.
 (1)、求直线的表达式;(2)、过动点且垂直于轴的直线与的交点分别为C,D,当点位于点上方时,写出的取值范围.16. 根据市场需求,某书城准备购进甲、乙两种青少年喜欢的读本进行销售,它们的进价和售价如下表.
(1)、求直线的表达式;(2)、过动点且垂直于轴的直线与的交点分别为C,D,当点位于点上方时,写出的取值范围.16. 根据市场需求,某书城准备购进甲、乙两种青少年喜欢的读本进行销售,它们的进价和售价如下表.读本
进价(元/本)
售价(元/本)
甲
30
45
乙
20
30
现计划用不超过1850元购进这两种读本共80本,并将这80本读本全部售完,
设购进甲种读本x本,这两种读本的总利润为y元.
(1)、求y与x的函数关系式.(2)、该书城如何进货才能获得最大利润?最大利润是多少?17. 在平面直角坐标系xOy中,已知直线与x轴相交于点A,与y轴相交于点B,点C在线段AB上(不与点A,B重合),以C为顶点的抛物线经过点B.(1)、求点A,B的坐标.(2)、求b,c的值.18. 近年来,市民交通安全意识逐步增强,头盔需求量增大.某商店购进甲、乙两种头盔,已知购买甲种头盔20只﹐乙种头盔30只,共花费2920元,甲种头盔的单价比乙种头盔的单价高11元.(1)、甲、乙两种头盔的单价各是多少元?(2)、商店决定再次购进甲、乙两种头盔共40只,正好赶上厂家进行促销活动,促销方式如下:甲种头盔按单价的八折出售,乙种头盔每只降价6元出售.如果此次购买甲种头盔的数量不低于乙种头盔数量的一半,那么应购买多少只甲种头盔,使此次购买头盔的总费用最小?最小费用是多少元?19. 在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象由函数 , x的图象向下平移1个单位得到.(1)、求这个一次函数的表达式.(2)、当x>-2时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=kx+b的值,直接写出m的取值范围.20. 如图①, 直线 与 轴、 轴分别交于点 , , 抛物线的顶点 在直线 上, 与 轴的交点为 , 其中点 的坐标为 , 直线 与直线 相交于点 . (1)、 如图 ②, 若抛物线经过原点 .
(1)、 如图 ②, 若抛物线经过原点 .①求该抛物线的函数表达式.
② 求 的值.
(2)、 连结 与 能否相等?若能, 求符合条件的点 的横坐标; 若不能, 请说明理由.四、综合题
-
21. 某太阳能热水器水箱的最大蓄水量为160升,在没有放水的情况下匀速注水.已知水箱的蓄水量y(升)与注水时间x(分)
x(分)
0
4
8
12
……
y(升)
20
60
100
140
……
 (1)、通过描点法判断变量x,y是否满足或近似地满足一次函数关系式.如果是,求y关于x的函数表达式.(2)、按上述速度注满水箱,需要多少分钟?22. A,B两地相距200千米.早上8:00货车甲从A地出发将一批物资运往B地,行驶一段路程后出现故障,即刻停车与B地联系.B地收到消息后立即派货车乙从B地出发去接运甲车上的物资.货车乙遇到甲后,用了18分钟将物资从货车甲搬运到货车乙上,随后开往B地.两辆货车离开各自出发地的路程y(千米)与时间x(小时)的函数关系如图所示.(通话等其他时间忽略不计)
(1)、通过描点法判断变量x,y是否满足或近似地满足一次函数关系式.如果是,求y关于x的函数表达式.(2)、按上述速度注满水箱,需要多少分钟?22. A,B两地相距200千米.早上8:00货车甲从A地出发将一批物资运往B地,行驶一段路程后出现故障,即刻停车与B地联系.B地收到消息后立即派货车乙从B地出发去接运甲车上的物资.货车乙遇到甲后,用了18分钟将物资从货车甲搬运到货车乙上,随后开往B地.两辆货车离开各自出发地的路程y(千米)与时间x(小时)的函数关系如图所示.(通话等其他时间忽略不计)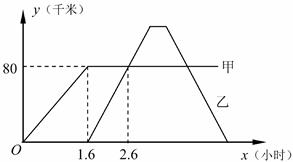 (1)、求货车乙在遇到货车甲前,它离开出发地的路程y关于x的函数表达式.(2)、因实际需要,要求货车乙到达B地的时间比货车甲按原来的速度正常到达B地的时间最多晚1个小时,问货车乙返回B地的速度至少为每小时多少千米?23. 如图1,抛物线()与轴交于 , 两点,与轴交于点 .
(1)、求货车乙在遇到货车甲前,它离开出发地的路程y关于x的函数表达式.(2)、因实际需要,要求货车乙到达B地的时间比货车甲按原来的速度正常到达B地的时间最多晚1个小时,问货车乙返回B地的速度至少为每小时多少千米?23. 如图1,抛物线()与轴交于 , 两点,与轴交于点 . (1)、求抛物线的解析式;(2)、点P在抛物线上,点Q在x轴上,以B,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;(3)、如图2,抛物线顶点为D,对称轴与x轴交于点E,过点的直线(直线除外)与抛物线交于G,H两点,直线 , 分别交x轴于点M,N.试探究是否为定值,若是,求出该定值;若不是,说明理由.
(1)、求抛物线的解析式;(2)、点P在抛物线上,点Q在x轴上,以B,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;(3)、如图2,抛物线顶点为D,对称轴与x轴交于点E,过点的直线(直线除外)与抛物线交于G,H两点,直线 , 分别交x轴于点M,N.试探究是否为定值,若是,求出该定值;若不是,说明理由.