广东省佛山市顺德区容桂街道2023-2024学年七年级下学期数学期中试题
试卷更新日期:2024-05-15 类型:期中考试
一、选择题(10个题,每题3分,共30分)
-
1. (-2024)0=( )A、-2024 B、1 C、0 D、20242. 如图,直线AB、CD相交于点O , 若∠1=30°,则∠2的度数是( )
 A、30° B、40° C、60° D、150°3. 2023年10月26日神舟十七号载人飞船在酒泉卫星发射中心圆满发射成功.此次神舟十七号载人飞船航天员空间站还将进行一系列科学实验,包括“空间蛋白质分子组装与应用研究”.其中某一蛋白质分子的直径仅0.000000028米,这个数用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 水中涟漪(圆形水波)不断扩大,记它的半径为r , 则圆周长C与r的关系式为C=2πr . 在上述变化中,自变量是( )A、2 B、半径r C、π D、周长C6. 下列各式能用平方差公式计算的是( )A、 B、 C、 D、7. 如图,下列条件能说明的是( )
A、30° B、40° C、60° D、150°3. 2023年10月26日神舟十七号载人飞船在酒泉卫星发射中心圆满发射成功.此次神舟十七号载人飞船航天员空间站还将进行一系列科学实验,包括“空间蛋白质分子组装与应用研究”.其中某一蛋白质分子的直径仅0.000000028米,这个数用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 水中涟漪(圆形水波)不断扩大,记它的半径为r , 则圆周长C与r的关系式为C=2πr . 在上述变化中,自变量是( )A、2 B、半径r C、π D、周长C6. 下列各式能用平方差公式计算的是( )A、 B、 C、 D、7. 如图,下列条件能说明的是( ) A、∠1=∠2 B、∠2=∠4 C、∠1=∠4 D、∠1+∠3=180°8. 等腰三角形一边长9cm,另一边长4cm,它第三边是( )A、4cm B、5cm C、9cm D、12cm9. 用一块含角的透明直角三角板画已知的边BC上的高,下列三角板的摆放位置正确的是( )A、
A、∠1=∠2 B、∠2=∠4 C、∠1=∠4 D、∠1+∠3=180°8. 等腰三角形一边长9cm,另一边长4cm,它第三边是( )A、4cm B、5cm C、9cm D、12cm9. 用一块含角的透明直角三角板画已知的边BC上的高,下列三角板的摆放位置正确的是( )A、 B、
B、 C、
C、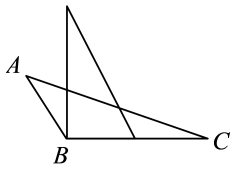 D、
D、 10. 下列图形能够直观地解释的是( )A、
10. 下列图形能够直观地解释的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题(5个题,每题3分,共15分
-
11. 计算:= .12. 如果一个角是40°,那么它的补角的度数是°.13. 体育课上某同学跳远的情况如图所示,直线l表示起跳线,经测量,PB=3.3米,PC=3.1米,PD=3.5米,则该同学的实际跳远成绩是米.
 14. 如图,正方形边长为12cm,在四个角分别剪去同样的等腰直角三角形.当三角形的直角边由小变大时,阴影部分的面积变化如下表所示:
14. 如图,正方形边长为12cm,在四个角分别剪去同样的等腰直角三角形.当三角形的直角边由小变大时,阴影部分的面积变化如下表所示:
三角形的直角边/cm
1
2
3
4
5
6
阴影部分的面积/cm2
142
136
126
112
94
72
若等腰直角三角形的直角边长为3cm,则图中阴影部分的面积是cm2 .
15. 为增强学生体质,感受中国的传统文化,某学校将国家级非物质文化遗产—“抖空竹”引入阳光特色大课间.下面图1是某同学“抖空竹”时的一个瞬间,小聪把它抽象成图2的数学问题:已知AB∥CD , ∠EAB=70°,∠ECD=100°,则∠E的度数是°.
三、解答题(9个题,共75分
-
16. 计算:17. 只用无刻度的直尺,在方格纸中画出两条互相垂直的直线,请画出两个不同类型的图形.
 18. 用三个相同的三角尺拼成如下的图形,请写出图中的所有平行线,并选择其中一组说明理由.
18. 用三个相同的三角尺拼成如下的图形,请写出图中的所有平行线,并选择其中一组说明理由. 19. 先化简,再求值: , 其中 , .20. 如图,在△ABC中,∠A=62°,∠B=74°,CD是∠ACB的角平分线.
19. 先化简,再求值: , 其中 , .20. 如图,在△ABC中,∠A=62°,∠B=74°,CD是∠ACB的角平分线. (1)、尺规作图:以点D为顶点,射线DA为一边,在∠ABC的内部作∠ADE=∠ABC , DE交AC于点E;(保留作图痕迹,不写作法)(2)、在(1)的条件下,求∠EDC的度数.21. 如图,在长为4a-1,宽为3b+2的长方形铁片上,剪去一个长为3a-2,宽为2b的小长方形铁片.
(1)、尺规作图:以点D为顶点,射线DA为一边,在∠ABC的内部作∠ADE=∠ABC , DE交AC于点E;(保留作图痕迹,不写作法)(2)、在(1)的条件下,求∠EDC的度数.21. 如图,在长为4a-1,宽为3b+2的长方形铁片上,剪去一个长为3a-2,宽为2b的小长方形铁片. (1)、计算剩余部分(即阴影部分)的面积;(2)、当a=4,b=3时,求阴影部分的面积.22. 综合与实践
(1)、计算剩余部分(即阴影部分)的面积;(2)、当a=4,b=3时,求阴影部分的面积.22. 综合与实践如图1所示的长方形ABCD的一边DC作左右匀速平行移动,图2反映它的边BC的长度l(cm)随时间t(s)变化而变化的情况,请解答下列问题:
 (1)、观察图2,当DC没有运动时,BC边的长度是 , 请你根据图象呈现的规律写出0至5秒间l与t的关系式 .(2)、根据图2,请描述一下DC边的运动情况.(3)、下表反映变化过程中,长方形ABCD的面积S()随时间t(s)变化的情况,并根据表中呈现的规律回答下列问题:
(1)、观察图2,当DC没有运动时,BC边的长度是 , 请你根据图象呈现的规律写出0至5秒间l与t的关系式 .(2)、根据图2,请描述一下DC边的运动情况.(3)、下表反映变化过程中,长方形ABCD的面积S()随时间t(s)变化的情况,并根据表中呈现的规律回答下列问题:DC边的运动时间/s
0
2
4
5
8
9
10
12
13
14
长方形ABCD的
面积/
80
120
160
180
180
150
a
60
30
0
①AB的长是 ▲ ;
②表格中a的值是 ▲ ;
③写出8至14秒间S()与t(s)的关系式.
23. 综合应用在学习《完全平方公式》时,某兴趣小组发现:已知a+b=5,ab=3,可以在不求a、
b的值的情况下,求出a2+b2的值.具体做法如下:
.
(1)、若a+b=7,ab=6,则a2+b2=;(2)、若m满足 , 求的值,同样可以应用上述方法解决问题.具体操作如下:解:设m=a , 8﹣m=b ,
则a+b=m+(8﹣m)=8,ab=m(8﹣m)=3,
所以 .
请参照上述方法解决下列问题:
①若 , 求的值;
②若 , 求的值;
(3)、如图,某校园艺社团在三面靠墙的空地上,用长11米的篱笆(不含墙AD)围成一个长方形的花圃ABCD , 面积为15平方米,其中墙AD足够长,墙AB⊥墙AD , 墙DC⊥墙AD . 随着学校社团成员的增加,学校在花圃ABCD旁分别以AB , CD边向外各扩建两个正方形花圃,以BC边向外扩建一个正方形花圃(扩建部分如图所示虚线区域部分),求花圃扩建后增加的面积. 24. 综合探究
24. 综合探究如图1,已知两条直线AB , CD被直线EF所截,分别交于点E , 点F , EM平分∠AEF交CD于点M , 且∠FEM=∠FME .
 (1)、直线AB与直线CD平行吗?说明你的理由;(2)、点G是射线MD上一动点(不与点M , F重合),EH平分∠FEG交CD于点H , 过点H作HN⊥EM于点N , 设∠EHN=α , ∠EGF=β .
(1)、直线AB与直线CD平行吗?说明你的理由;(2)、点G是射线MD上一动点(不与点M , F重合),EH平分∠FEG交CD于点H , 过点H作HN⊥EM于点N , 设∠EHN=α , ∠EGF=β .①当点G在点F的右侧时,请根据题意,在图2中补全图形,并求出当β=60°时α的度数;
②当点G在运动过程中,α和β之间有怎样的数量关系?请写出你的猜想,并简单说明理由.