江西省赣州市瑞金市2023-2024学年七年级下学期数学期中试卷

试卷更新日期：2024-05-15 类型：期中考试

进入 出卷网 下载

一、选择题（本大题共6小题，每小题3分，共18分．每小题只有一个正确选项）

  • 1. 在数17 ， −π ， 0.314 ， 2 ， −64 ， 5中，无理数的个数有（ ）
    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 2. 下列等式正确的是（ ）
    A、±9=3 B、6+3=9 C、(−3)2=3 D、9=±3

    查看试题解析

  • 3. 在平面直角坐标系中，将点A(a,−2)先向左平移1个单位，再向上平移3个单位得到点B.若B的横纵坐标相等，则a的值为（ ）
    A、0 B、1 C、2 D、3

    查看试题解析

  • 4. 如图，先在纸上画两条直线a ， b ， 使a∥b ， 再将一块直角三角板平放在纸上，使其直角顶点落在直线b上，若∠2=50° ， 则∠1的度数是（ ）

    A、30° B、40° C、50° D、60°

    查看试题解析

  • 5. 如图，直线m∥n ， 点A、C在直线m上，点B在直线n上，BC平分∠ABD ， 若∠BAC=122° ， 则∠ACB的度数为（ ）

    A、58° B、61° C、30° D、29°

    查看试题解析

  • 6. 在平面直角坐标系中，AB∥x轴，AB=2 ， 若点A(1 ， −3) ， 则点B的坐标是（ ）
    A、(1 ， −1) B、(1 ， −5)或(1 ， −1) C、(3 ， −3) D、(−1 ， −3)或(3 ， −3)

    查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

  • 7. 16的算术平方根是

    查看试题解析

  • 8. 已知点P(2,m2+1) ， 则该点位于第象限．

    查看试题解析

  • 9. 如图，将数−5 ， 7 ， 13表示在数轴上，其中能被墨迹覆盖的数是 ．

    查看试题解析

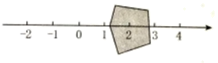  • 10. 平面直角坐标系中，若点P(4−m,3m)在y轴上，则点P的坐标为 ．

    查看试题解析

  • 11. 如图，用一张等宽的纸条折成如下图所示的图案，若∠1=23° ， 则∠2的度数为 ．

    查看试题解析

  • 12. 如图，直线EF上有两点A、C ， 分别引两条射线AB、CD ， ∠DCF=60° ， ∠EAB=70° ， 射线AB、CD分别绕A点，C点以1度/秒和3度秒的速度同时顺时针转动，在射线CD转动一周的时间内，使得CD与AB平行所有满足条件的时间＝ ．

    查看试题解析

三、（本大题共5小题，每小题6分，共30分）

  • 13.
    (1)、计算：−83−(3)2−64；
    (2)、解方程：2x2=8

    查看试题解析

  • 14. 已知实数a+9的一个平方根是−5 ， 2b−a的立方根是−2 ．
    (1)、求a、b的值．
    (2)、求2a+b的平方根．

    查看试题解析

  • 15. 如图是天安门广场周围的主要景点分布示意图，在此图中建立平面直角坐标系，表示故宫的点的坐标为(0,−1) ， 表示美术馆的点的坐标为(2,2) ， 请你解答下列问题．

    (1)、请画出符合题意的平面直角坐标系；
    (2)、在平面直角坐标系内表示下列位置的坐标：

    天安门；

    电报大楼；

    王府井；

    中国国家博物馆 ．

    查看试题解析

  • 16. 完成下面推理过程：

    已知：如图，已知AB⊥AC ， DE⊥AC ， ∠B=∠D ．

    求证：AD∥BC ．

    证明：∵AB⊥AC ， DE⊥AC ， （已知）

    ∴ ▲ ∥ ▲  ．

    ∴∠B=∠DEC ． （ ）

    又∵∠B=∠D ， （已知）

    ∴∠D= ▲  ． （ ）

    ∴AD∥BC ． （ ）

    查看试题解析

  • 17. 在平面直角坐标系中，已知点P(m+2,m−3)。
    (1)、若点P在x轴上，则m的值为；
    (2)、若点P位于第四象限，且点P到x轴的距离等于2，求点P的坐标．

    查看试题解析

四、（本大题共3小题，每小题8分，共24分）

  • 18. 如图，已知∠DEB＝100°，∠BAC＝80°．

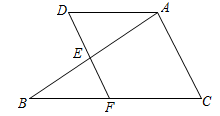    (1)、判断DF与AC的位置关系，并说明理由；
    (2)、若∠ADF＝∠C ， ∠DAC＝120°，求∠B的度数．

    查看试题解析

  • 19. 我们知道2是无理数，因此2的小数部分我们不可能全部写出来，于是小明用2−1来表示2的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理的，因为√2的整数部分是1，将这个数减去其整数部分，差就是小数部分．又例如：4<5<9即2<5<3 ， 所以5的整数部分为2，小数部分为5−2 ， 诱根据以上信息，回答下列问题：
    (1)、34整数部分是 ， 小数部分是；
    (2)、如果11的整数部分为a ， 7−7的整数部分为b ， 求12a+7b的立方根．

    查看试题解析

  • 20. 如图，数轴上有A、B、C三点，表示1和2的对应点分别为A、B ， 点B到点A的距离与点C到原点O的距离相等．

    (1)、AB的长为；点C表示的数为：；
    (2)、求BC的长．

    查看试题解析

五、（本大题共2小题，每小题9分，共18分）

  • 21. 如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别为A(−2,3) ， B(−3,1) ， C(0,−2) ．

    (1)、将△ABC向右平移4个单位后得到△A1B1C1 ， 请画出△A1B1C1；
    (2)、△ABC的面积＝；
    (3)、定义：在平面直角坐标系中，横坐标与纵坐标都是整数的点称为“整点”，请直接写出△A1B1C1内部所有的整点的坐标 ．

    查看试题解析

  • 22. 已知点A(a,0)、B(b,0) ， 且a+4+|b−2|=0 ．

    (1)、求a、b的值．
    (2)、在y轴的正半轴上找一点c ， 使得三角形ABC的面积是15，求出点C的坐标．
    (3)、过（2）中的点C作直线MN∥x轴，在直线MN上是否存在点D ， 使得三角形ACD的面积是三角形ABC面积的12？若存在，求出点D的坐标；若不存在，请说明理由．

    查看试题解析

六、（本大题共12分）

  • 23. 已知AB∥CD ， 点P是平面内一点，过点P作射线PN、PM ， PM与AB相交于点B ．

    (1)、如图1，若点P为直线CD上一点，∠ABM=45° ， ∠CPN=30° ， 求∠MPN的度数：
    (2)、如图2，若点P为直线AB、CD之间区域的一点，射线PN交CD于点E ， ∠ABM和∠CEP的角平分线交于点F ． 请说明：2∠BFE+∠MPN=180°；
    (3)、如图3，若点P、H是直线CD上的点，连接HB并延长交∠MPN的角平分线于点Q ， 射线PN交AB于点G ， 设∠BGP=α ． 当∠PHB=∠PBH时，请直接用含a的代数式表示∠PQH ．

    查看试题解析