广东省湛江市经济技术开发区2023-2024学年八年级下学期数学期中试题

试卷更新日期：2024-05-15 类型：期中考试

进入出卷网下载

一、选择题：（本题共10小题，每小题3分，共30分）。

1. 下列根式是最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{12}$ C、 $\sqrt{4.5}$ D、 $\sqrt{5}$

查看试题解析
2. 以下列各数为边长，能构成直角三角形的是（）

A、1，1，2 B、1， $\sqrt{3}$ ， 2 C、4，5，6 D、2， $\sqrt{3}$ ， $\sqrt{5}$

查看试题解析
3. 如图，下列条件中，不能确定四边形ABCD是平行四边形的是（）

A、 $A B = C D$ ， $A D ∥ B C$ B、 $A B = C D$ ， $A B ∥ C D$ C、 $A B ∥ C D$ ， $A D ∥ B C$ D、 $A B = C D$ ， $A D = B C$

查看试题解析
4. 下列运算，结果正确的是（）

A、 $\sqrt{5} - \sqrt{3} = \sqrt{2}$ B、 $3 + \sqrt{2} = 3 \sqrt{2}$ C、 $\sqrt{6} \div \sqrt{2} = 3$ D、 $\sqrt{6} \times \sqrt{2} = 2 \sqrt{3}$

查看试题解析
5. 如图，在△ABC中， $∠ A C B = 90 °$ ， D为边AB的中点， $B C = 6$ ， $A C = 8$ ，则CD长为（）

A、2 B、3 C、4 D、5

查看试题解析
6. 对于四边形的以下说法：
①对角线互相平分的四边形是平行四边形；
②对角线相等且互相平分的四边形是矩形；
③对角线垂直且互相平分的四边形是菱形；
④顺次连接对角线相等的四边形各边的中点所得到的四边形是矩形．
其中你认为正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为16cm，则正方形A ， B ， C ， D的面积之和为（）cm² ．

A、16 B、256 C、32 D、64

查看试题解析
8. 如图，在菱形ABCD中，对角线AC与BD相交于点O，且AC＝12，BD＝16，则菱形的高AE为（）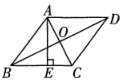

A、9.6 B、4.8 C、10 D、5

查看试题解析
9.
如图，在Rt△ABC中，∠A＝90°，P为边BC上一动点，PE⊥AB于E ， PF⊥AC于F ，动点P从点B出发，沿着BC匀速向终点C运动，则线段EF的值大小变化情况是（　　）.

A、一直增大 B、一直减小 C、先减小后增大 D、先增大后减少

查看试题解析
10. 如图，在赵爽弦图中，已知直角三角形的短直角边长为 $a$ ，长直角边长为 $b$ ，大正方形的面积为20，小正方形的面积为4，则 $a b$ 的值是（）

A、10 B、9 C、8 D、7

查看试题解析

二、填空题：（本题共6小题，每小题3分，共18分）

11. 式子 $\sqrt{x - 4}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 计算： $3 \sqrt{6} + \sqrt{2} - 2 \sqrt{6} - 3 \sqrt{2} =$ ．

查看试题解析
13. $▱$ ABCD中，若 $∠ A : ∠ B = 2 : 3$ ，则 $∠ C =$ ．

查看试题解析
14. 如图，在 $▱$ ABCD中， $A D = 6$ ， E为AD上一动点，M ， N分别为BE ， CE的中点，则MN的长为．

查看试题解析
15. 如图，菱形ABCD ，点A、B、C、D均在坐标轴上， $∠ A B C = 120 °$ ，点 $A (- 3, 0)$ ，点E是CD的中点，点P是OC上的一动点，则 $P D + P E$ 的最小值是．

查看试题解析
16. 已知：如图，正方形ABCD中， $A B = 2$ ， AC ， BD相交于点O ， E ， F分别为边BC ， CD上的动点（点E ， F不与线段BC ， CD的端点重合）．且 $B E = C F$ ，连接OE ， OF ， EF ．在点E ， F运动的过程中，有下列四个说法：①△OEF是等腰直角三角形；②△OEF面积的最小值是1；③至少存在一个△ECF ，使得△ECF的周长是 $2 + \sqrt{3}$ ；④四边形OECF的面积是1．其中正确的是．

查看试题解析

三、解答题：（本大题共8小题，共72分）

17.

(1)、计算： $(\begin{array}{l} \sqrt{3} + \sqrt{2} \end{array}) (\begin{array}{l} \sqrt{3} - \sqrt{2} \end{array}) + (\sqrt{12} - \sqrt{\frac{1}{3}}) \times \sqrt{6}$

(2)、如果最简二次根式 $\sqrt{3 a - 8}$ 与 $\sqrt{17 - 2 a}$ 是同类二次根式，求a的值．

查看试题解析
18. 如图，在四边形 $A B C D$ 中， $∠ B = 90 °$ ， $A B = B C = 2$ ， $A D = 1$ ， $C D = 3$ ．

(1)、求 $∠ D A B$ 的度数．

(2)、求四边形 $A B C D$ 的面积．

查看试题解析
19. 如图，已知 $▱$ ABCD ．

(1)、尺规作图：延长BC并在BC的延长线上截取线段CE ，使得 $C E = B C$ （保留作图痕迹，不要求写作法）；

(2)、在（1）的条件下，连结AE ，交CD于点F ，求证： $△ A F D ≌ △ E F C$ ．

查看试题解析
20.
如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF．求证：四边形DEBF是平行四边形．

查看试题解析
21. 在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ．点D是边AB上的一点，连接CD．作 $A E ∥ D C$ ， $C E ∥ A B$ ，连接ED．

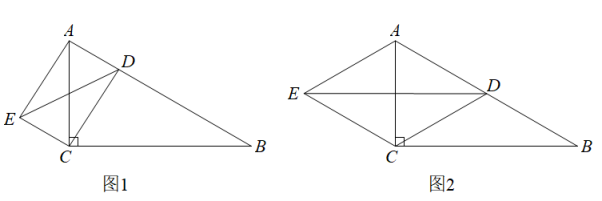(1)、如图1，当 $C D ⊥ A B$ 时，求证： $A C = E D$ ；

(2)、如图2，当D是边AB的中点时，若 $A B = 10$ ， $E D = 8$ ，求四边形ADCE的面积．

查看试题解析
22. 如图：是长方形纸片ABCD折叠的情况，纸片的宽度 $A B = 8$ cm，长 $A D = 10$ cm，AD沿点A对折，点D正好落在BC上的M处，AE是折痕．

(1)、求CM的长；

(2)、求梯形ABCE的面积．

查看试题解析
23. 在进行二次根式化简时，我们有时会碰上如 $\frac{5}{\sqrt{3}}$ ， $\sqrt{\frac{2}{3}}$ ， $\frac{2}{\sqrt{3} + 1}$ 一样的式子，这样的式子我们可以将其进一步化简： $\frac{5}{\sqrt{3}} = \frac{5 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{5 \sqrt{3}}{3}$ ， $\sqrt{\frac{2}{3}} = \sqrt{\frac{2 \times 3}{3 \times 3}} = \frac{\sqrt{6}}{3}$ ， $\frac{2}{\sqrt{3} + 1} = \frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \sqrt{3} - 1$ ；以上这种化简的方法叫做分母有理化，请利用分母有理化解答下列问题：

(1)、化简： $\frac{2}{\sqrt{5} + \sqrt{3}}$ ；

(2)、若a是 $\sqrt{2}$ 的小数部分，求 $\frac{3}{a}$ 的值；

(3)、矩形的面积为 $3 \sqrt{5} + 1$ ，一边长为 $\sqrt{5} - 2$ ，求它的周长．

查看试题解析
24. 在菱形ABCD中， $∠ A = 60 °$ ，点E ， F分别是边AB ， BC上的点．

(1)、【尝试初探】如图1，若 $∠ E D F = 60 °$ ，求证： $D E = D F$ ；

(2)、【深入探究】如图2，点G ， H分别是边CD ， AD上的点，连接EG与FH相交于点O且 $∠ E O F = 60 °$ ，求证： $E G = F H$

(3)、【拓展延伸】如图3，若点E为AB的中点， $A B = 6$ ， $B F = 1$ ．
①设 $D H = x$ ， $C G = y$ ，请用关于x的代数式表示y；
②若 $C G + D H = 6$ ，求EG的长．

查看试题解析