江西省吉安市十校联盟2023-2024学年八年级下学期数学期中试卷-在线组卷题库

1. 下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（）

A、赵爽弦图 B、笛卡尔心形线 C、科克曲线 D、斐波那契螺旋线

查看试题解析
2. 若 $a < b$ ，则下列不等式一定成立的是( )

A、 $a - 1 < b - 1$ B、 $- a < - b$ C、 $| a | < | b |$ D、 $a^{2} < b^{2}$

查看试题解析
3. 等腰三角形的一个内角是 $10 0^{°}$ ，则这个等腰三角形的底角是( )

A、 $10 0^{°}$ B、 $4 0^{°}$ C、 $10 0^{°}$ 或 $4 0^{°}$ D、 $4 0^{°}$ 或 $2 0^{°}$

查看试题解析
4. 如图： $△ A B C$ 中，AD平分 $∠ B A C, D E ⊥ A B$ 于点 $E, S_{△ A B C} = 8, D E = 2, A B = 5$ ，则 $A C =$ ( )

A、4 B、5 C、3 D、2

查看试题解析
5. 如图， $△ A B C$ 在平面直角坐标系中第二象限内，顶点 $A$ 的坐标是 $(- 2, 3)$ ，先把 $△ A B C$ 向右平移4个单位得到 $△ A_{1} B_{1} C_{1}$ ，再作 $△ A_{1} B_{1} C_{1}$ 关于 $x$ 轴对称图形 $△ A_{2} B_{2} C_{2}$ ，则顶点 $A_{2}$ 的坐标是( )

A、 $(- 3, 2)$ B、 $(2, - 3)$ C、 $(1, - 2)$ D、 $(- 1, 2)$

查看试题解析
6. 如图，在平面直角坐标系中，将边长为 $a$ 的正方形OABC绕点O顺时针旋转 $4 5^{°}$ 后得到正方形 $O A_{1} B_{1} C_{1}$ .依此方式连续旋转2024次得到正方形 $O A_{2024} B_{2024} C_{2024}$ ，那么点 $A_{2024}$ 的坐标是( )

A、 $(a, 0)$ B、 $(\frac{\sqrt{2}}{2} a, - \frac{\sqrt{2}}{2} a)$ C、 $(- \frac{\sqrt{2}}{2} a, - \frac{\sqrt{2}}{2} a)$ D、 $(0, a)$

查看试题解析

7. 命题“若 $a^{2} > b^{2}$ ，则 $a > b$ ”的逆命题是命题(填“真”或“假”).

查看试题解析
8. 一次函数 $y = - \frac{3}{2} x + 3$ 的图象如图所示，当 $- 3 < y < 3$ 时， $x$ 的取值范围是.

查看试题解析
9. 如图，在三角形纸片ABC中， $∠ B A C = 9 0^{°}, A B = 2, A C = 3$ .沿过点 $A$ 的直线将纸片折叠，使点 $B$ 落在边BC上的点 $D$ 处；再将纸片折叠，使点 $C$ 与点 $D$ 重合，折痕与AC的交点为 $E$ ，则 $A E$ 的长是.

查看试题解析
10. 如图，在 $△ A B C$ 中，点 $D$ 在边BC上， $D E ⊥ A B$ 于点 $E, D F ⊥ B C$ ，交AC于点 $F, B D = C F, B E = C D$ .若 $∠ A F D = 14 5^{°}$ ，则 $∠ E D F =$ .

查看试题解析
11. 已知关于 $x$ 的不等式组 ${\begin{array}{l} - x + a < 2 \\ \frac{3 x - 1}{2} \leq x + 1 \end{array}$ 只有三个整数解，则 $a$ 的取值范围是.

查看试题解析
12. 如图，O是等边三角形ABC内一点， $∠ A O B = 10 5^{°}, ∠ B O C = α$ ，将 $△ B O C$ 绕点 $C$ 按顺时针方向旋转 $6 0^{°}$ 得到 $△ A D C$ ，连接OD.若 $△ A O D$ 是等腰三角形，则 $α$ 的度数为.

查看试题解析

13. 解不等式组 ${\begin{array}{l} 3 x + 4 \leq 3 - (1 - 2 x) \\ 1 - \frac{x - 1}{2} > \frac{x + 2}{3} \end{array}$ ，并把解集表示在数轴上.

查看试题解析
14. 如图所示，点 $A$ ，点 $B$ 的坐标分别为 $(0, - 2), (- 4, 0)$ ，将线段AB平移至CD，所得点 $C$ ，点 $D$ 坐标分别为 $(1, a), (b, 3)$ .

(1)、求a ， b的值；

(2)、求线段AB平移的距离.

查看试题解析
15. 如图，函数 $y = 2 x$ 和 $y = a x + 4$ 的图象交于点 $A (m, 3)$ ，求不等式组 ${\begin{array}{l} a x + 4 \leq 2 x \\ a x + 4 > 0 \end{array}$ 的解集.

查看试题解析
16. 如图，已知在△ABC中，∠A＝60°，∠C＝90°，将△ABC绕点B顺时针旋转150°，得到△DBE ．请仅用无刻度的直尺，按要求画图（保留画图痕迹，在图中标出字母，并在图下方表示出所画图形）．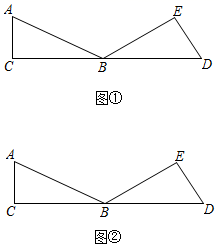

(1)、在图①中，画一个等边三角形；

(2)、在图②中，画一个等腰直角三角形．

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ A C B = 9 0^{°}$ ，将 $△ A B C$ 绕点 $C$ 顺时针旋转得到 $△ D E C$ ，旋转角为 $α$ ， CD ， DE分别交AB于点F ， G ，连接BD.

(1)、求证： $∠ A G D = α$ ；

(2)、若 $B C = 2, a = 3 0^{°}$ ， $B D / / A C$ ，求AB的长.

查看试题解析

18. 根据实数乘法（除法）法则可知：
①若 $a b > 0$ （或 $\frac{a}{b} > 0$ ），则 ${\begin{array}{l} a > 0 \\ b > 0 \end{array}$ 或 ${\begin{array}{l} a < 0 \\ b < 0 \end{array}$ ；
②若 $a b < 0$ (或 $\frac{a}{b} < 0)$ ，则 ${\begin{array}{l} a > 0 \\ b < 0 \end{array}$ 或 ${\begin{array}{l} a < 0 \\ b > 0 \end{array}$ ；
根据上述知识，求不等式 $(x - 2) (x + 3) > 0$ 的解集的过程如下：
解：原不等式可化为① ${\begin{array}{l} x - 2 > 0 \\ x + 3 > 0 \end{array}$ 或② ${\begin{array}{l} x - 2 < 0 \\ x + 3 < 0 \end{array}$ .
解①得： $x > 2$ ；
解②得： $x < - 3$ ；
$∴$ 原不等式的解集为 $x < - 3$ 或 $x > 2$ .
请你运用所学知识，结合上述内容解答下面的问题：

(1)、不等式 $(x + 1) (x - 3) < 0$ 的解集为.

(2)、求不等式 $\frac{x + 4}{1 - x} ＜ 0$ 的解集(要求写出解答过程).

查看试题解析
19. 如图，在四边形ABCD中， $A D / / B C, ∠ B = ∠ D$ ，点 $E$ 在BA的延长线上，连接CE.

(1)、试说明：∠E=∠ECD；

(2)、若 $∠ E = 6 0^{°}$ ， CE平分 $∠ B C D$ ，求证： $△ E C B$ 为等边三角形.

查看试题解析
20. 如图，在 $△ A B C$ 中，DE ， DF分别为BC ， AB边的垂直平分线，连接AD ， CD.

(1)、若 $∠ B = 4 0^{°}$ ，求 $∠ A C D$ 的度数；

(2)、判断 $∠ B$ 与 $∠ A C D$ 之间的数量关系，并说明理由.

查看试题解析

21. 某公交公司有A ， B型两种客车，它们的载客量和租金如下表：

$A$
$B$
载客量（人/辆）
45
30
租金（元/辆）
400
300
红星中学根据实际情况，计划租用A ， B型客车共7辆，同时送七年级师生到基地校参加社会实践活动，设租用 $A$ 型客车 $x$ 辆，根据要求回答下列问题：

(1)、用含 $x$ 的式子填写下表：

车辆数(辆)
载客量
租金(元)
$A$
$x$
45x
400x
$B$
$7 - x$
①
②

(2)、若要保证租车费用不超过2700元，求 $x$ 的最大值；

(3)、在(2)的条件下，若七年级师生共有283人，写出最省钱的租车方案.

查看试题解析
22. 如图， $△ A B C$ 和 $△ A M N$ 均为等边三角形，将 $△ A Y N$ 绕点 $A$ 旋转( $△ A M N$ 在直线AC的右侧).

(1)、求证：△BAM≌△CAN；

(2)、若点C，M，N在同一条直线上，
①求∠BMC的度数：
②点M是CN的中点，求证：BM⊥AC.

查看试题解析

23. 在Rt $△ A B C$ 中， $A C = B C, ∠ A C B = 9 0^{°}$ ，将线段CA绕点 $C$ 旋转 $α$ $(0^{°} < α < 9 0^{°})$ ，得到线段CD ，连接AD、BD.

(1)、如图1，将线段CA绕点 $C$ 逆时针旋转 $α$ ，则 $∠ A D B =$ °；

(2)、如图2，将线段CA绕点 $C$ 顺时针旋转 $a$ 时，
①求证： $∠ A D B = 4 5^{°}$ ；
②若 $∠ B C D$ 的平分线CE交BD于点 $F$ ，交DA的延长线于点 $E$ ，连结BE ，如图3，用等式表示线段AD、CE、BE之间的数量关系，并证明.

查看试题解析

江西省吉安市十校联盟2023-2024学年八年级下学期数学期中试卷

一、选择题(本大题共6小题,每小题3分,共18分)

二、选择题(本大题共6小题,每小题3分,共18分)

三、解答题(本大题共5个小题,每小题6分,共30分)

四、（本大题共3小题，每小题8分，共24分）

五、(本大题共2小题,每小题9分,共18分)

六、(本大题共12分)

	车辆数(辆)	载客量	租金(元)
$A$	$x$	45x	400x
$B$	$7 - x$	①	②

	$A$	$B$
载客量（人/辆）	45	30
租金（元/辆）	400	300