江西省九江市都昌县2023-2024学年八年级下学期数学期中试卷

试卷更新日期：2024-05-15 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共18分）

1. 下列图形中，既是轴对称图形，又是中心对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 当0＜x＜1时，x²、x、 $\frac{1}{x}$ 的大小顺序是（　　）

A、x² $< x < \frac{1}{x}$ B、 $\frac{1}{x}$ ＜x＜x² C、 $\frac{1}{x} < x^{2}$ ＜x D、x＜x²＜ $\frac{1}{x}$

查看试题解析
3. 已知点 $A (a, 1)$ 与点 $A^{'} (5, b)$ 关于坐标原点对称，则实数a ， b的值是（）

A、 $a = - 5, b = - 1$ B、 $a = - 5, b = 1$ C、 $a = 5, b = - 1$ D、 $a = 5, b = 1$

查看试题解析
4. 如图，AD是△ ABC中∠ BAC的角平分线，DE⊥AB于点E，S_△ABC＝7，DE＝2， AB＝4，则AC长是（）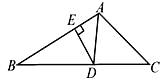

A、3 B、4 C、6 D、5

查看试题解析
5. 如图，在矩形ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD，AC于点E，O，连接CE，则CE的长为（）

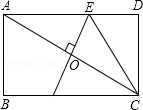A、3 B、3.5 C、2.5 D、2.8

查看试题解析
6. 如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法中正确的个数是
①AD是∠BAC的平分线；②∠ADC=60°；③点D在AB的中垂线上；④S_△DAC：S_△ABC=1：3.

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（每小题3分，共18分）

7. 已知一等腰三角形的两边x ， y满足 $| x - 4 | + \sqrt{y - 8} = 0$ ，则该等腰三角形的周长为．

查看试题解析
8. 解不等式组 ${\begin{array}{l} 5 x - 1 < 3 x + 3 \\ 3 x + 15 > x + 7 \end{array}$ ，并写出它的所有整数解的和．

查看试题解析
9. 函数 $y = m x + n$ 和函数 $y = k x$ 在同一坐标系中的图象如图所示，则关于 $x$ 的不等式 $m x + n >$ kx的解集是．

查看试题解析
10. 不等式组 ${\begin{array}{l} x > - 1 \\ x < m \end{array}$ 有2个整数解，则 $m$ 的取值范围是．

查看试题解析
11. 如图，将 $△ A B C$ 绕着点 $C$ 顺时针方向旋转 $4 0^{°}$ 后得到 $△ A^{'} B^{'} C$ ．若 $∠ A = 4 0^{°}, ∠ B^{'} = 11 0^{°}$ ，则 $∠ B C A^{'}$ 的度数是．

查看试题解析
12. 如图，等边三角形ABC中，D、E分别在AB、BC边上，且 $A D = B E, A E$ 与CD交于点 $F, A G ⊥$ CD于点 $G$ ．下列结论：① $A E = C D$ ；② $∠ A F C = 12 0^{°}$ ；③ $△ A D F$ 是等腰三角形；④ $\frac{F G}{A G} = \frac{1}{2}$ ，其中正确的结论是．

查看试题解析

三、解答题（第13－17题每题6分，第18－20题每题8分，第21、22题每题9分，第23题12分，共84分）

13. 解下列不等式（组）：

(1)、 $\frac{x - 2}{2} \geq \frac{7 - x}{3}$

(2)、 ${\begin{matrix} - x + 3 < 2 x \\ \frac{x + 1}{5} - \frac{x - 2}{2} \geq 0 \end{matrix}$ ，并把它的解集表示在数轴上．

查看试题解析
14. 如图，在△ABC中，AB＝AC，AD是BC边上的中线，延长CB至点E，延长BC至点F，使BE＝CF，连接AE、AF．
求证：AD平分∠EAF．

查看试题解析
15. 如图，D为△ABC边BC延长线上一点，且CD=CA ， E是AD的中点，CF平分∠ACB交AB于点F ．求证：CE⊥CF ．

查看试题解析
16. 如图，在平面直角坐标系中，△ABC的三个顶点分别为A（－1，－1），B（－3，3），C（－4，1）

(1)、画出△ABC关于y轴对称的△A₁B₁C₁ ，并写出点B的对应点B₁的坐标；

(2)、画出△ABC绕点A按顺时针旋转90°后的△AB₂C₂ ，并写出点C的对应点C₂的坐标．

查看试题解析
17. 如图，将Rt△ABC沿某条直线折叠，使斜边的两个端点A与B重合，折痕为DE ．

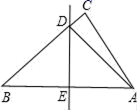(1)、如果AC＝6cm ， BC＝8cm ，试求△ACD的周长；

(2)、如果∠CAD：∠BAD＝1：2，求∠B的度数．

查看试题解析
18. 某水果商行计划购进A、B两种水果共200箱，这两种水果的进价、售价如下表所示：
进价（元/箱）
售价（元/箱）
A
60
70
B
40
55

(1)、若该商行进货总额为1万元，则两种水果各购进多少箱？

(2)、若商行规定A种水果进货箱数不低于B种水果进货箱数的 $\frac{1}{3}$ ，应怎样进货才能使这批水果售完后商行获利最多？此时利润为多少？

查看试题解析
19. 已知在△ABC中，∠ACB的平分线CD交AB于点D ， $D E / / B C$ ．

(1)、如图1，求证：△CDE是等腰三角形；

(2)、如图2，若DE平分∠ADC交AC于E ， ∠ABC=30°，在BC边上取点F使BF=DF ，若BC=12，求DF的长．

查看试题解析
20. 已知：如图△ABC中AB=6cm，AC=8cm，BD平分∠ABC ， CD平分∠ACB ，过D作直线平行于BC ，交AB ， AC于E ， F ．

(1)、若∠BDC=110°，求∠A的度数；

(2)、若BE=CF ，求证：点D是EF的中点；

(3)、求△AEF的周长．

查看试题解析
21. 如图，在△ABC中，MP ， NO分别垂直平分AB ， AC．

(1)、若BC=10cm ，试求出△PAO的周长；

(2)、若AB=AC ， ∠BAC=110°，试求∠PAO的度数；

(3)、在（2）中，若无AB=AC的条件，你能求出∠PAO的度数吗？若能，请求出来；若不能，请说明理由．

查看试题解析
22. 去年夏天，某地区遭受到罕见的水灾，“水灾无情人有情”，某单位给该地区某中学捐献一批饮用水和蔬菜共320件，其中饮用水比蔬菜多80件．

(1)、求饮用水和蔬菜各有多少件．

(2)、现计划租用甲、乙两种型号的货车共8辆，一次性将这批饮用水和蔬菜全部运往这所中学已知每辆甲型货车最多可装饮用水40件和蔬菜10件，每辆乙型货车最多可装饮用水和蔬菜各20件，则该单位安排甲、乙两种型号的货车时有几种方案？请你帮忙设计出来．

(3)、在（2）的条件下，如果甲型货车每辆需付运费400元，乙型货车每辆需付运费360元，该单位选择哪种方案可使运费最少？最少运费是多少？

查看试题解析
23. 如图，在△ABC中，AC=BC=2，∠C=90°，将一块等腰三角板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点．如图①、②、③是旋转三角板得到的图形中的3种情况，研究：

(1)、三角板绕点P旋转，观察线段PD与PE之间有什么数量关系？结合图②说明理由．

(2)、三角板绕点P旋转，△PCE是否能成为等腰三角形？若能，写出所有情况（求BE的长度）．

查看试题解析

	进价（元/箱）	售价（元/箱）
A	60	70
B	40	55