河北省石家庄市新乐市2024年中考模拟数学试题
试卷更新日期:2024-05-15 类型:中考模拟
一、选择题(本大题共16个小题,共38分.1—6小题各3分;7—16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
-
1. 点到x轴的距离是( )A、2 B、-4 C、-2 D、42. 化简结果正确的是( )A、1 B、 C、 D、3. -8的立方根是( )A、 B、2 C、-2 D、不存在4. 若 , 则括号内应填的单项式是( )A、a B、 C、 D、5. 解不等式 , 下列在数轴上表示的解集正确的是( ).A、
 B、
B、 C、
C、 D、
D、 6. 中国的探月、登月计划受到世人的关注,中国人何时在月球上留下第一行脚印,在这里插上鲜艳的五星红旗?月球与地球之间的平均距离约为38.4万公里,38.4万用科学记数法表示为( )A、 B、 C、 D、7. 已知 , 则与k最接近的整数为( )A、3 B、4 C、5 D、68. 如图,正五边形内接于 , 连接 , 则( )
6. 中国的探月、登月计划受到世人的关注,中国人何时在月球上留下第一行脚印,在这里插上鲜艳的五星红旗?月球与地球之间的平均距离约为38.4万公里,38.4万用科学记数法表示为( )A、 B、 C、 D、7. 已知 , 则与k最接近的整数为( )A、3 B、4 C、5 D、68. 如图,正五边形内接于 , 连接 , 则( )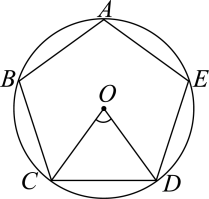 A、 B、 C、 D、9. 如图,在中,以点O为圆心,5为半径作弧,分别交射线OA , OB于点C , D , 再分别以C , D为圆心,CO的长为半径作弧,两弧在内部交于点E , 作射线OE , 若 , 则C , D两点之间的距离为( )
A、 B、 C、 D、9. 如图,在中,以点O为圆心,5为半径作弧,分别交射线OA , OB于点C , D , 再分别以C , D为圆心,CO的长为半径作弧,两弧在内部交于点E , 作射线OE , 若 , 则C , D两点之间的距离为( ) A、5 B、 C、6 D、810. 在一次体育课上,小明随机调查了30名同学投篮20次投中的次数,数据如下表所示:
A、5 B、 C、6 D、810. 在一次体育课上,小明随机调查了30名同学投篮20次投中的次数,数据如下表所示:投篮20次投中的次数
6
7
9
12
人数
6
7
10
7
则投篮20次投中的次数的中位数和众数分别是( )
A、8,9 B、10,9 C、7,12 D、9,911. 如图,在四边形OABC中, , , , 则点B到OC的距离为( ) A、 B、 C、1 D、212. 几个大小相同,且棱长为1的小正方体所搭成几何体的俯视图如图所示,图中小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图的面积为( )
A、 B、 C、1 D、212. 几个大小相同,且棱长为1的小正方体所搭成几何体的俯视图如图所示,图中小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图的面积为( )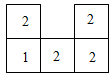 A、3 B、4 C、6 D、913. 为测量一池塘两端A,B间的距离,甲、乙两位同学分别设计了两种不同的方案.
A、3 B、4 C、6 D、913. 为测量一池塘两端A,B间的距离,甲、乙两位同学分别设计了两种不同的方案.甲:如图1,先过点B作的垂线 , 再在射线上取C,D两点,使 , 接着过点D作的垂线 , 交的延长线于点E,则测出的长即为A,B间的距离;
乙:如图2,先确定直线 , 过点B作射线 , 在射线上找可直接到达点A的点D,连接 , 作 , 交直线于点C,则测出的长即为A,B间的距离,则下列判断正确的是( )
 A、只有甲同学的方案可行 B、只有乙同学的方案可行 C、甲、乙同学的方案均可行 D、甲、乙同学的方案均不可行14. 今年假期,小星一家驾车前往西柏坡旅游,在行驶过程中,汽车离西柏坡景点的路程y(km)
A、只有甲同学的方案可行 B、只有乙同学的方案可行 C、甲、乙同学的方案均可行 D、甲、乙同学的方案均不可行14. 今年假期,小星一家驾车前往西柏坡旅游,在行驶过程中,汽车离西柏坡景点的路程y(km)与所用时间x(h)之间的函数关系的图象如图所示,下列说法正确的是( )
 A、小星家离西柏坡景点的路程为50km B、小星从家出发第1小时的平均速度为25km/h C、小星从家出发2小时离景点的路程为125km D、小星从家到西柏坡景点的时间共用了3h15. 如图,在平行四边形 中, , , , 是对角线 上的动点,且 , , 分别是边 ,边 上的动点.下列四种说法:
A、小星家离西柏坡景点的路程为50km B、小星从家出发第1小时的平均速度为25km/h C、小星从家出发2小时离景点的路程为125km D、小星从家到西柏坡景点的时间共用了3h15. 如图,在平行四边形 中, , , , 是对角线 上的动点,且 , , 分别是边 ,边 上的动点.下列四种说法:①存在无数个平行四边形 ;
②存在无数个矩形 ;
③存在无数个菱形 ;
④存在无数个正方形 .其中正确的个数是( )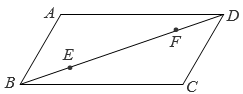 A、1 B、2 C、3 D、416. 经过两点的抛物线(为自变量)与轴有交点,则线段长为( )A、10 B、12 C、13 D、15
A、1 B、2 C、3 D、416. 经过两点的抛物线(为自变量)与轴有交点,则线段长为( )A、10 B、12 C、13 D、15二、填空题(本大题有3个小题,共12分.17小题2分,18-19小题各4分,每空2分,把答案写在题中横线上)
-
17. 已知关于x , y的二元一次方程组的解满足 , 则m的值为;18. 记反比例函数的图象为L , 其上有两点 , , k为正数.(1)、当时,有 , 则k的取值范围是;(2)、在(1)成立的情况下,若k为整数,过点作平行与x轴的直线交L于点M , 则点M的横坐标可为;(写出一个即可)19. 如图,已知四个正六边形摆放在图中,顶点A , B , C , D , E , F在圆上,其中上下两个大一点的正六边形边长均为a , 左右两个正六边形边长均为b .
 (1)、;(2)、若 , 则 .
(1)、;(2)、若 , 则 .三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
-
20. 嘉琪参加寒假实习活动,与公司约定一个月(30天)的报酬是M型平板电脑一台和1500元现金,当她工作满20天后因故结束实习,结算工资时公司给了她一台该型平板电脑和300元现金.(1)、这台M型平板电脑价值多少元?(2)、嘉琪若工作m天,将上述工资支付标准折算为现金,她应获得多少报酬(用含m的代数式表示)?21. 每个人都拥有一个快乐数字,我们把自己出生的年份减去组成这个年份的数字之和,所得的差就是我们自己的快乐数字.比如我国著名的数学家华罗庚出生于1910年,他的快乐数字是 .(1)、某人出生于1949年,他的快乐数字是;(2)、你再举几个例子并观察,这些快乐数字都能被_▲_整除,请你用所学知识说明你的猜想.(3)、请你重新对快乐数字定义,并写出一个你找到的规律(直接写出结果,不用证明).22. 打造书香文化,培养阅读习惯,我市某中学计划在各班建图书角,开展“我最喜欢阅读的书篇”为主题的调查活动,学生根据自己的爱好选择一类书籍(A:科技类,B:文学类,C:政史类,D:艺术类,E:其他类).张老师组织数学兴趣小组对学校部分学生进行了问卷调查,根据收集到的数据,绘制了两幅不完整的统计图(如图所示).

根据图中信息,请回答下列问题;
(1)、条形图中的 , , 文学类书籍对应扇形圆心角等于度;(2)、若该校有2000名学生,请你估计最喜欢阅读政史类书籍的学生人数;(3)、甲同学从A,B,C三类书籍中随机选择一种,乙同学从B,C,D三类书籍中随机选择一种,请用画树状图或者列表法求甲乙两位同学选择相同类别书籍的概率.23. 如图,在直角坐标系中,点在直线上,过点A的直线交y轴于点 . (1)、求m的值和直线的函数表达式.(2)、若点在线段AB上,点在直线上,求的最小值.24.
(1)、求m的值和直线的函数表达式.(2)、若点在线段AB上,点在直线上,求的最小值.24.已知I是的内心,AI的延长线交的外接圆于点D , 连接DC , DB .
 (1)、在图1中:①证明:;②判断外心的位置,并证明;(2)、如图2,若AB为的外接圆直径,取AB中点O , 且于点I , DE切圆O于点D , 求的值.
(1)、在图1中:①证明:;②判断外心的位置,并证明;(2)、如图2,若AB为的外接圆直径,取AB中点O , 且于点I , DE切圆O于点D , 求的值.
