山东省济南市高新区2023-2024学年八年级下学期数学期中考试试卷

试卷更新日期：2024-05-15 类型：期中考试

进入出卷网下载

一、选择题（本大题共10个小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

1. “二十四节气”是中华上古农耕文明的智慧结晶．下列四幅标识图，其中文字上面图案是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各式由左边到右边的变形中，是因式分解的是（　　）

A、a（x﹣y）＝ax﹣ay B、a²﹣b²＝（a+b）（a﹣b） C、x²﹣4x+3＝x（x﹣4）+3 D、a²+1＝a（a+ $\frac{1}{a}$ ）

查看试题解析
3.
如图，四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）

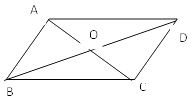A、AB∥DC， AD∥BC B、AB∥DC， AD=BC C、AO=CO，BO=DO D、AB=DC，AD=BC

查看试题解析
4. 如图，将 $△ A B C$ 沿 $B C$ 向右平移得到 $△ D E F$ ，若 $B C = 5$ ， $B E = 2$ ，则 $C F$ 的长是（）

A、2 B、 $2.5$ C、3 D、5

查看试题解析
5. 如果分式 $\frac{x y}{2 x - 3 y}$ 中的x，y都扩大为原来的2倍，那么分式的值（）

A、扩大为原来的2倍 B、扩大为原来的4倍 C、不变 D、不能确定

查看试题解析
6. 如图 4×4 的正方形网格中，其中一个三角形①绕某点旋转一定的角度，得到三角形②，则其旋转中心是（）

A、点 A B、点 B C、点 C D、点 D

查看试题解析
7. 如图，将△ABC绕点A逆时针旋转70°，得到△ADE ，若点D在线段BC的延长线上，则∠B的大小是（）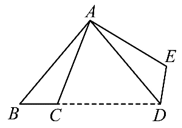

A、45° B、55° C、60° D、100°

查看试题解析
8. 如图，y₁ ， y₂分别表示某一品牌燃油汽车和电动汽车所需费用y（单位：元）与行驶路程S（单位：千米）的关系，燃油汽车花费25元和电动汽车花费10元的行车里程数相同．已知燃油汽车每千米所需的费用比电动汽车每千米所需的费用的2倍多0.1元，设电动汽车每千米所需的费用为x元，则可列方程为（　　）

A、 $\frac{25}{2 x - 0.1} = \frac{10}{x}$ B、 $\frac{25}{x} = \frac{10}{2 x - 0.1}$ C、 $\frac{25}{x} = \frac{10}{2 x + 0.1}$ D、 $\frac{25}{2 x + 0.1} = \frac{10}{x}$

查看试题解析
9. 如图，在△ABC中，AB＝6，将△ABC 绕点B按逆时针方向旋转 30° 后得到△A₁BC₁ ，则阴影部分的面积为（　　）

A、6 B、 $6 \sqrt{3}$ C、 $9 \sqrt{3}$ D、9

查看试题解析
10. 已知y₁＝ $\frac{1}{x - 1}$ ，且y₂＝ $\frac{1}{1 - y_{1}}$ ， y₃＝ $\frac{1}{1 - y_{2}}$ ， y₄＝ $\frac{1}{1 - y_{3}}$ ⋯y_n＝ $\frac{1}{1 - y_{n - 1}}$ ，则y₂₀₂₄为（　　）

A、 $\frac{1}{x - 1}$ B、2﹣x C、 $\frac{x - 1}{x - 2}$ D、 $\frac{x - 2}{x - 1}$

查看试题解析

二、填空题：（本大题共6个小题，每小题4分，共24分．）

11. 分解因式4xy﹣6xz＝．

查看试题解析
12. 在平面直角坐标系中，点M（2，﹣6）向上移动5个单位长度后的对应点M^'的坐标是．

查看试题解析
13. 如图，▱ABCD的对角线AC ， BD相交于点O ， AC+BD＝18，AB＝7．则△OCD的周长为．

查看试题解析
14.
夏季荷花盛开，为了便于游客领略“人从桥上过，如在河中行”的美好意境，某景点拟在如图所示的矩形荷塘上架设小桥．若荷塘周长为280m，且桥宽忽略不计，则小桥总长为m．

查看试题解析
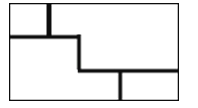15. 若关于x的方程 $\frac{a x}{x - 2} - 1 = \frac{4}{x - 2}$ 无解，则a的值是．

查看试题解析
16. 在四边形ABCD中，AD∥BC ， BC⊥CD ， AD＝6cm ， BC＝10cm ， M是BC上一点，且BM＝4cm ，点E从A出发以1cm/s的速度向D运动，点F从点B出发以2cm/s的速度向点C运动，当其中一点到达终点，而另一点也随之停止，设运动时间为t ，当t的值为时，以A、M、E、F为顶点的四边形是平行四边形．

查看试题解析

三、解答题：（本大题共10个小题，共86分．解答应写出文字说明、证明过程或演算步骤．）

17. 分解因式：

(1)、16﹣b²；

(2)、3ax²﹣6axy+3ay² ．

查看试题解析
18. 解分式方程： $\frac{x}{x - 3} - 1 = \frac{18}{x^{2} - 9}$ ．

查看试题解析
19. 先化简，再求值：求： $(\frac{a}{a - 1} - 1) \div \frac{a^{2} + 2 a + 1}{a^{2} - 1}$ ，在1，﹣1，2四个数中选一个适合的数，说明理由并代入求值．

查看试题解析
20. 在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上，请解答下列问题：

(1)、作出△ABC向左平移4个单位长度后得到的△A₁B₁C₁ ，并写出点C₁的坐标；

(2)、作出△ABC关于原点O对称的△A₂B₂C₂ ，并写出点C₂的坐标；

(3)、△A₂B₂C₂可看作△A₁B₁C₁以点（，）为旋转中心，旋转180°得到的．

查看试题解析
21. 如图，已知▱ABCD ， DE是∠ADC的角平分线，交BC于点E ．

(1)、求证：CD＝CE；

(2)、若点E是BC的中点，∠C＝108°，求∠BAE的度数．

查看试题解析
22. 如图，▱ABCD中，E、F为对角线BD上的两点，且DF＝BE ，连接AE ， CF ．

(1)、求证：∠DAE＝∠BCF ．

(2)、连接AF、CE ，求证：四边形AECF是平行四边形．

查看试题解析
23. 在数学课上，老师出了这样一道题：甲、乙两地相距1400km ，乘高铁列车从甲地到乙地比乘特快列车少用9h ，已知高铁列车的平均行驶速度是特快列车的2.8倍，求高铁列车从甲地到乙地的时间．
老师要求同学先用列表方式分析再解答．下面是两个小组分析时所列的表格
小组甲：设特快列车的平均速度为x km/h
时间/h
平均速度/（km/h）
路程/km
高铁列车
____
____
1400
特快列车
____
x
1400
小组乙：高铁列车从甲地到乙地的时间为yh ．
时间/h
平均速度/（km/h）
路程/km
高铁列车
y
____
1400
特快列车
____
____
1400

(1)、根据题意，填写表格中空缺的量；

(2)、结合表格，选择一种方法进行解答．

查看试题解析
24. 综合与实践：
数形结合思想是根据数与形之间的对应关系，通过数与形的相互转化来解决数学问题的思想．我们常利用数形结合思想，借助形的几何直观性来阐明数之间某种关系，如：探索整式乘法的一些法则和公式．
探索整式乘法的一些法则和公式．

(1)、探究一：将图1的阴影部分沿虚线剪开后，拼成图2的形状，拼图前后图形的面积不变，因此可得一个多项式的分解因式．

(2)、探究二：类似地，我们可以借助一个棱长为a的大正方体进行以下探索：
在大正方体一角截去一个棱长为b（b＜a）的小正方体，如图3所示，则得到的几何体的体积为；

(3)、将图3中的几何体分割成三个长方体①、②、③，如图4，图5所示，∵BC＝a ， AB＝a﹣b ， CF＝b ， ∴长方形①的体积为ab（a﹣b）．类似地，长方体②的体积为，长方体③的体积为；（结果不需要化简）

(4)、用不同的方法表示图3中几何体的体积，可以得到的恒等式（将一个多项式因式分解）为．

(5)、问题应用：利用上面的结论，解决问题：已知a﹣b＝6，ab＝2，求a³﹣b³的值．

查看试题解析
25. 【阅读理解】我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，解决问题的策略一般要进行一定的转化，其中“作差法”就是常用的方法之一，“作差法”：就是通过作差、变形，利用差的符号确定它们的大小，即要比较代数式M ， N的大小，只要作出差M﹣N ，若M﹣N＞0，则M＞N；若M﹣N＝0，则M＝N；若M﹣N＜0，则M＜N ．
【解决问题】

(1)、若n＞0，试判断： $\frac{n + 1}{n} - \frac{n + 2}{n + 1}$ 0（填“＞”，“＝”或“＜”）；

(2)、已知 $A = \frac{m^{2} + 6 m + 9}{m^{2} - 9}$ ， $B = \frac{2 m + 1}{2 m + 6}$ ，当m＞﹣3时，试比较 $\frac{1}{A}$ 与B的大小，并说明理由；

(3)、嘉嘉和琪琪两次购物均买了同一种商品，嘉嘉两次都买了m千克该商品，琪琪两次购买该商品均花费n元，已知第一次购买该商品的价格为a元/千克，第二次购买该商品的价格为b元/千克（a ， b是整数，且a≠b）．请用作差法比较嘉嘉和琪琪两次所购买商品的平均价格的高低．

查看试题解析
26. 我们可以通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整．
原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF＝45°，连接EF ，则EF＝BE+DF ，试说明理由．

(1)、思路梳理
∵AB＝AD ，
∴把△ABE绕点A逆时针旋转90°至△ADG ，可使AB与AD重合．
∵∠ADC＝∠B＝90°，
∴∠FDG＝180°，点F、D、G共线．
易证△AFE≌ ，得EF＝BE+DF ．

(2)、类比引申
如图2，四边形ABCD中，AB＝AD ， ∠BAD＝90°，点E、F分别在边BC、CD上，∠EAF＝45°．若∠B、∠D都不是直角，则当∠B+∠D＝180°时，是否仍有EF＝BE+DF ，并说明理由．

(3)、联想拓展
如图3，在△ABC中，∠BAC＝90°，AB＝AC ，点D、E均在边BC上，且∠DAE＝45°．猜想BD、DE、EC应满足的等量关系，并写出推理过程．

查看试题解析

	时间/h	平均速度/（km/h）	路程/km
高铁列车	____	____	1400
特快列车	____	x	1400