重庆市五校联考2023-2024学年八年级下学期数学期中试卷

试卷更新日期：2024-05-15 类型：期中考试

进入出卷网下载

一、选择题（本大题共10个小题，每题4分，共40分）

1. 下列各式属于最简二次根式的有（）

A、 $\sqrt{8}$ B、 $\sqrt{x^{2} + 1}$ C、 $\sqrt{y^{3}}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
2. 下列几组数中，不能作为直角三角形三边的是（）

A、1， $\sqrt{2}$ ， $\sqrt{3}$ B、7，24，25 C、4，5，6 D、 $\frac{3}{5}$ ， $\frac{4}{5}$ ，1

查看试题解析
3. 下列计算正确的是（）

A、3 $\sqrt{2}$ ×4 $\sqrt{2}$ ＝12 $\sqrt{2}$ B、 $\sqrt{(- 9) \times (- 25)} = \sqrt{- 9} \times \sqrt{- 25} = (- 3) \times (- 5) = 15$ C、﹣3 $\sqrt{\frac{2}{3}}$ ＝ $\sqrt{{(- 3)}^{2} \times \frac{2}{3}}$ ＝6 D、 $\sqrt{13^{2} - 12^{2}} = \sqrt{(13 + 12) (13 - 12)}$ ＝5

查看试题解析
4. 下列关系中，是菱形的性质但不是平行四边形的性质的是（）

A、对角线垂直 B、两组对边分别平行 C、对角线互相平分 D、两组对角分别相等

查看试题解析
5. 在△ABC中，∠A：∠B：∠C＝1：1：2，a ， b ， c分别为∠A ， ∠B ， ∠C的对边，则下列说法中错误的是（）

A、∠C＝90° B、a²＝b²﹣c² C、c²＝2a² D、a＝b

查看试题解析
6. 下列判断中正确的是（）

A、四边相等的四边形是正方形 B、对角线相互垂直平分的平行四边形是正方形 C、四角相等的四边形是正方形 D、对角线互相垂直平分且相等的四边形是正方形

查看试题解析
7. 如图，正方形ABCD的对角线AC是菱形AEFC的一边，则∠FAB等于（）

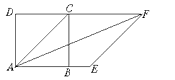A、135° B、45° C、22.5° D、30°

查看试题解析
8. 如图所示，长方形纸片ABCD中，AB＝5cm ， BC＝10cm ，现将其沿EF对折，使得点C与点A重合，则AF长（）

A、3cm B、 $2 \sqrt{5}$ cm C、5cm D、 $\frac{25}{4}$ cm

查看试题解析
9. 已知x+y＝﹣5，xy＝4，则 $\sqrt{\frac{y}{x}} + \sqrt{\frac{x}{y}}$ 的值是（）

A、 $- \frac{5}{2}$ B、 $\frac{5}{2}$ C、 $\pm \frac{5}{2}$ D、 $\frac{25}{4}$

查看试题解析
10. 如图，在菱形ABCD中，DE⊥AB ，垂足为E ， $\frac{D E}{A E} = \frac{3}{4}$ ， BE＝1，F是BC的中点．现有下列四个结论：①DE＝3；②四边形DEBC的面积等于9；③（AC+BD）（AC﹣BD）＝80；④DF＝DE ．其中正确结论的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共8个小题，每题4分，共32分）

11. 如果 $\sqrt{x + 8}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 在平面直角坐标系中，点A（﹣6，8）到原点的距离为．

查看试题解析
13. 若最简二次根式 $\sqrt{3 a + 1}$ 和 $\sqrt{4 a - 3}$ 可以合并，则a＝．

查看试题解析
14. 某人要登上6m高的建筑物，为确保安全，梯子底端要离开建筑物2.5m ，且顶端不低于建筑物顶部，则梯子长应不少于 m ．

查看试题解析
15. 如图，平行四边形ABCD中，∠BAC＝90°，AB＝3，AC＝4，则BD的长为 .

查看试题解析
16. 如图，矩形ABCD面积为40，点P在边CD上，PE⊥AC ， PF⊥BD ，垂足分别为E ， F ．若AC＝10，则PE+PF＝．

查看试题解析
17. 将一组数 $\sqrt{2}$ ， 2， $\sqrt{6}$ ， 2 $\sqrt{2}$ ， $\sqrt{10}$ ， …，2 $\sqrt{51}$ 按图中的方法排列：
$\sqrt{2}$ ， 2， $\sqrt{6}$ ， 2 $\sqrt{2}$ ， $\sqrt{10}$ ， 2 $\sqrt{3}$
$\sqrt{14}$ ， 4， $3 \sqrt{2}$ ， 2 $\sqrt{5}$ ， $\sqrt{22}$ ， 2 $\sqrt{6}$
$\sqrt{26}$ ， 2 $\sqrt{7}$ ， $\sqrt{30}$ ， 4 $\sqrt{2}$ ， $\sqrt{34}$ ， 6
若3 $\sqrt{2}$ 的位置记为（2，3），2 $\sqrt{7}$ 的位置记为（3，2），则这组数中最大有理数的位置记为．

查看试题解析
18. 如图，在正方形ABCD中，AD＝5，点E，F是正方形ABCD内的两点，且AE＝FC＝3，BE＝DF＝4，则EF的长为．

查看试题解析

三、解答题（本大题共8个小题，第19题8分，第20-26题各10分，共78分）

19. 计算

(1)、 $(3 \sqrt{15} + \sqrt{\frac{3}{5}})$ ÷ $\sqrt{5}$ ；

(2)、2a $\sqrt{3 a b^{2}}$ ﹣ $\frac{b}{9} \sqrt{27 a^{3}}$ +3ab $\sqrt{\frac{1}{3} a}$ (b>0)．

查看试题解析
20. 如图，Rt△ABC中，∠C＝90°．

(1)、用无刻度的直尺和圆规在边BC上找一点P ，使PA＝PB ．（请保留作图痕迹）

(2)、若AC＝6，BC＝8，计算（1）中线段CP的长．

查看试题解析
21. 若x ， y是实数，且y＝ $\sqrt{4 x - 1} + \sqrt{1 - 4 x}$ +3，求（ $\frac{2}{3} x \sqrt{9 x} + 2 \sqrt{x y}$ ）﹣（ $\sqrt{x^{3}} + \sqrt{25 x y}$ ）的值．

查看试题解析
22. 如图，已知G、H是△ABC的边AC的三等分点，GE∥BH ，交AB于点E ， HF∥BG交BC于点F ，延长EG、FH交于点D ，连接AD、DC ，设AC和BD交于点O ，求证：四边形ABCD是平行四边形．

查看试题解析
23. 在△ABC中，AB＝AC ， D是BC的中点，以AC为腰向外作等腰直角△ACE ， ∠EAC＝90°，连接BE ，交AD于点F ，交AC于点G ．

(1)、求证：∠AEB＝∠ACF；

(2)、试判断线段EF、BF与AC三者之间的等量关系，并证明你的结论．

查看试题解析
24. 如图，以正方形ABCD的CD边长作等边△DCE ， AC和BE交于点F ，连接DF ．

(1)、求∠AFD的度数；

(2)、求证：AF＝EF ．

查看试题解析
25. 小明在解决问题：已知a＝ $\frac{1}{2 + \sqrt{3}}$ ，求2a²﹣8a+1的值．
他是这样分析与解的：∵a＝ $\frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$
∴ $a - 2 = - \sqrt{3}$ ， ∴（a﹣2）²＝3，a²﹣4a+4＝3
∴a²﹣4a＝﹣1，∴2a²﹣8a+1＝2（a²﹣4a）+1＝2×（﹣1）+1＝﹣1．
请你根据小明的分析过程，解决如下问题：

(1)、 $\frac{1}{\sqrt{3} + \sqrt{2}}$ ＝， $\frac{1}{\sqrt{5} + \sqrt{3}}$ ＝．

(2)、化简： $\frac{1}{\sqrt{11} + \sqrt{9}} + \frac{1}{\sqrt{13} + \sqrt{11}} + \dots + \frac{1}{\sqrt{121} + \sqrt{119}}$ ．

(3)、若a＝ $\frac{1}{\sqrt{2} - 1}$ ，请按照小明的方法求出4a²﹣8a+1的值．

查看试题解析
26. 已知点O是△ABC内任意一点，连接OA并延长到点E ，使得AE＝OA ，以OB ， OC为邻边作平行四边形OBFC ，连接OF ，与BC交于点H ，连接EF ．

(1)、问题发现
如图1，若△ABC为等边三角形，线段EF与BC的位置关系是，数量关系为；

(2)、拓展探究
如图2，若△ABC为等腰直角三角形（BC为斜边），（1）中的两个结论是否成立？若成立，请给予证明；若不成立，请写出正确的结论再给予证明；

(3)、解决问题
如图3，若△ABC是等腰三角形，AB＝AC＝2，BC＝3，请你直接写出线段EF的长．

查看试题解析