云南省玉溪市易门县2024年中考数学一模试卷
试卷更新日期:2024-05-15 类型:中考模拟
一、选择题(本大题共15小题,每小题只有一个正确选项,每小题2分,共30分)
-
1. 冰箱保鲜室的温度零上5℃记作+5℃,则冷冻室的温度零下18℃记作( )A、﹣13℃ B、﹣18℃ C、+13℃ D、+18℃2. 长江干流上的葛洲坝、三峡向家坝、溪洛渡、白鹤滩、乌东德6座巨型梯级水电站,共同构成目前世界上最大的清洁能源走廊,总装机容量71695000千瓦,将71695000用科学记数法表示为( )A、 B、 C、 D、3. 直尺和三角板如图摆放, , 则的度数为( )
 A、 B、 C、 D、4. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A、 B、 C、 D、4. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( ) A、函数解析式为I= B、蓄电池的电压是18V C、当R=6Ω时,I=4A D、当I≤10A时,R≥3.6Ω5. 下列运算正确的是( )A、2a+b=2ab B、(﹣2x2)3=﹣8x5 C、2 D、6. 如图,在矩形ABCD中,若AB=6,AC=10,AE=2,则=( )
A、函数解析式为I= B、蓄电池的电压是18V C、当R=6Ω时,I=4A D、当I≤10A时,R≥3.6Ω5. 下列运算正确的是( )A、2a+b=2ab B、(﹣2x2)3=﹣8x5 C、2 D、6. 如图,在矩形ABCD中,若AB=6,AC=10,AE=2,则=( ) A、 B、 C、 D、7. 用数轴探究不等式组的解集,下面探究过程表示正确的是( )A、
A、 B、 C、 D、7. 用数轴探究不等式组的解集,下面探究过程表示正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图是某几何体的三视图,该几何体是( )
8. 如图是某几何体的三视图,该几何体是( ) A、长方体 B、正方体 C、圆柱 D、圆锥9. 一列单项式按以下规律排列:x , ﹣3x2 , 5x3 , ﹣7x4 , 9x5 , ﹣11x6 , 13x7 , …,则第2024个单项式是( )A、﹣4049x2024 B、4049x2024 C、﹣4047x2024 D、4047x202410. 某班篮球爱好小组10名队员进行定点投篮练习,每人投篮10次,将他们投中的次数进行统计,制成如表:
A、长方体 B、正方体 C、圆柱 D、圆锥9. 一列单项式按以下规律排列:x , ﹣3x2 , 5x3 , ﹣7x4 , 9x5 , ﹣11x6 , 13x7 , …,则第2024个单项式是( )A、﹣4049x2024 B、4049x2024 C、﹣4047x2024 D、4047x202410. 某班篮球爱好小组10名队员进行定点投篮练习,每人投篮10次,将他们投中的次数进行统计,制成如表:投中次数
2
3
5
6
7
8
人数
1
2
3
2
1
1
则关于这10名队员投中次数组成的数据,下列说法错误的是( )
A、平均数为5 B、中位数为5 C、众数为5 D、方差为511. 某班学生毕业时,每个同学都要给其他同学写一份留言纪念,全班同学共写了1980份留言,如果全班同学有x名学生,根据题意,下列方程正确的是( )A、x(x﹣1)=1980 B、x(x+1)=1980 C、 D、12. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 13. 如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点连接AF,BF,∠AFB =90°,且AB=8,BC= 14,则EF的长是 ( )
13. 如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点连接AF,BF,∠AFB =90°,且AB=8,BC= 14,则EF的长是 ( ) A、2 B、3 C、4 D、514. 使有意义的x的取值范围是( )A、x>3 B、x<3 C、x≥3 D、x≤315. 筒车是我国古代发明的一种水利灌溉工具,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且 被水面截得弦 长为4米, 半径长为3米.若点C为运行轨道的最低点,则点C到弦 所在直线的距离是( )
A、2 B、3 C、4 D、514. 使有意义的x的取值范围是( )A、x>3 B、x<3 C、x≥3 D、x≤315. 筒车是我国古代发明的一种水利灌溉工具,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且 被水面截得弦 长为4米, 半径长为3米.若点C为运行轨道的最低点,则点C到弦 所在直线的距离是( ) A、1米 B、2米 C、 米 D、 米
A、1米 B、2米 C、 米 D、 米二、填空题(本大题共4小题,每小题2分,共8分)
-
16. |﹣6|的相反数是 .17. 分解因式:xy2﹣4x= .18. 为了解学生的阅读情况,对某校六年级部分学生的阅读情况展开调查,并列出了相应的频数分布直方图(如图所示)(每组数据含最小值,不含最大值)(0﹣1小时4人,1﹣2小时10人,2﹣3小时14人,3﹣4小时16人,4﹣5小时6人),若共有200名学生,则该学校六年级学生阅读时间不低于3小时的人数是 .
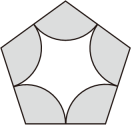
 19. 如图,已知正五边形的边长为 , 则阴影部分的面积为 .
19. 如图,已知正五边形的边长为 , 则阴影部分的面积为 .
三、解答题(本大题共8小题,共62分)
-
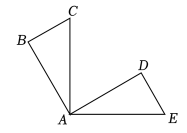
20. 计算:21. 如图,已知 , , , , 求证: .
 22. 随着科技的发展,油电混合动力汽车已经开始普及.某种型号的油电混合动力汽车,从A地到B地纯燃油行驶费用78元,从A地到B地纯用电行驶费用28元,已知每行驶1km , 纯燃油费用比纯用电费用多0.5元.求每行驶1km纯用电的费用.23. 4张相同的卡片上分别写有数字0、1、﹣2、3,将卡片的背面朝上,洗匀后从中任意抽取1张,将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.(1)、第一次抽取的卡片上数字是非负数的概率为 ;(2)、小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜;否则,乙获胜.小敏设计的游戏规则公平吗?为什么?(请用树状图或列表等方法说明理由)24. 如图,在矩形ABCD中,对角线AC、BD相交于点O , 在AB的延长线上找一点E , 连接EC , 使得EC=AC .
22. 随着科技的发展,油电混合动力汽车已经开始普及.某种型号的油电混合动力汽车,从A地到B地纯燃油行驶费用78元,从A地到B地纯用电行驶费用28元,已知每行驶1km , 纯燃油费用比纯用电费用多0.5元.求每行驶1km纯用电的费用.23. 4张相同的卡片上分别写有数字0、1、﹣2、3,将卡片的背面朝上,洗匀后从中任意抽取1张,将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.(1)、第一次抽取的卡片上数字是非负数的概率为 ;(2)、小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜;否则,乙获胜.小敏设计的游戏规则公平吗?为什么?(请用树状图或列表等方法说明理由)24. 如图,在矩形ABCD中,对角线AC、BD相交于点O , 在AB的延长线上找一点E , 连接EC , 使得EC=AC . (1)、求证:四边形BDCE是平行四边形;(2)、若AB=6,BC=8,求点E到AC的距离.25. 为增强学生体质,让学生享受阳光体育大课间活动,某学校准备采购甲、乙两种跳绳供学生使用.经询价,现有一家商场对甲种跳绳的出售价格根据购买量给予优惠,对乙种跳绳按25元/根的价格出售,设该学校购买甲种跳绳x根,付款y元,y与x之间的函数关系如图所示.
(1)、求证:四边形BDCE是平行四边形;(2)、若AB=6,BC=8,求点E到AC的距离.25. 为增强学生体质,让学生享受阳光体育大课间活动,某学校准备采购甲、乙两种跳绳供学生使用.经询价,现有一家商场对甲种跳绳的出售价格根据购买量给予优惠,对乙种跳绳按25元/根的价格出售,设该学校购买甲种跳绳x根,付款y元,y与x之间的函数关系如图所示. (1)、求出y与x之间的函数关系式;(2)、若该学校计划一次性购买甲,乙两种跳绳共100根,且甲种跳绳不少于40根,但又不超过60根,如何分配甲,乙两种跳绳的购买量,才能使该校付款总金额w最少?26. 在平面直角坐标系xOy中,抛物线y=mx2+2mx﹣3m+2.(1)、求抛物线的对称轴;(2)、①过点P(0,2)作与x轴平行的直线,交抛物线于点M , N . 求点M , N的坐标;
(1)、求出y与x之间的函数关系式;(2)、若该学校计划一次性购买甲,乙两种跳绳共100根,且甲种跳绳不少于40根,但又不超过60根,如何分配甲,乙两种跳绳的购买量,才能使该校付款总金额w最少?26. 在平面直角坐标系xOy中,抛物线y=mx2+2mx﹣3m+2.(1)、求抛物线的对称轴;(2)、①过点P(0,2)作与x轴平行的直线,交抛物线于点M , N . 求点M , N的坐标;②横、纵坐标都是整数的点叫做整点.如果抛物线和线段MN围成的封闭区域内(不包括边界)恰有3个整点,求m的取值范围.
27. 如图,在⊙O中,弦AB与弦CD相交于点G , OA⊥CD于点E , 过点B的直线与CD的延长线交于点F , AC∥BF . (1)、若∠FGB=∠FBG , 求证:BF是⊙O的切线;(2)、若tan∠F= , CD=24,求⊙O的半径;(3)、请问的值为定值吗?若是,请写出计算过程,若不是,请说明理由.
(1)、若∠FGB=∠FBG , 求证:BF是⊙O的切线;(2)、若tan∠F= , CD=24,求⊙O的半径;(3)、请问的值为定值吗?若是,请写出计算过程,若不是,请说明理由.