湖北省武汉市江夏区2023-2024学年七年级下学期数学月考试卷

试卷更新日期：2024-05-14 类型：月考试卷

进入出卷网下载

一、单选题

1. 估计与 $\sqrt{40}$ 最接近的整数是( )

A、4 B、7 C、6 D、5

查看试题解析
2. 下列说法不正确的是（）

A、 $\frac{1}{25}$ 的平方根是 $\pm \frac{1}{5}$ B、 $- 9$ 是81的一个平方根 C、 $0.2$ 的算术平方根是 $0.04$ D、 $- 27$ 的立方根是 $- 3$

查看试题解析
3. 如图，过△ABC的顶点A作BC边上的高，下列作法正确的是（）

A、 B、 C、 D、

查看试题解析
4. 木工师傅用图中的角尺画平行线，他依据的数学道理是( )

A、同位角相等，两直线平行 B、内错角相等，两直线平行 C、同旁内角互补，两直线平行 D、以上结论都不正确

查看试题解析
5. 如图，以下说法错误的是( )

A、若 $∠ E A D = ∠ B$ ，则 $A D / / B C$ B、若 $∠ E A D + ∠ D = 180 °$ ，则 $A B / / C D$ C、若 $∠ C A D = ∠ B C A$ ，则 $A D / / B C$ D、若 $∠ D = ∠ E A D$ ，则 $A B / / C D$

查看试题解析
6. 如图，直线 $a // b$ ，一块含60°角的直角三角板ABC(∠A＝60°)按如图所示放置.若∠1＝55°，则∠2的度数为（）

A、105° B、110° C、115° D、120°

查看试题解析
7. 如图，把两个面积为1dm²的小正方形分别沿对角线剪开，将所得的4个直角三角形拼接在一起，就得到一个面积为2dm²的大正方形，这个大正方形的边长是（　　）

A、1 B、1.5 C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
8. 下列命题：①过一点有且只有一条直线与已知直线平行；②垂直于同一条直线的两条直线互相平行；③相等的角是对顶角；④平行于同一条直线的两条直线互相平行．其中是真命题有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，在同一平面内有n条直线两两相交，当 $n = 2$ 时邻补角的对数计为 $a_{1}$ ，当 $n = 3$ 时邻补角的对数计为 $a_{2}$ ，当 $n = 4$ 时邻补角的对数计为 $a_{3}$ _···以此类推当 $n = 2024$ 时邻补角的对数计为 $a_{2023}$ .则 $\frac{1}{a_{^{1}}} + \frac{1}{a_{^{2}}} + \frac{1}{a_{^{3}}} +$ … $+ \frac{1}{a_{^{2023}}}$ 的值为( )

A、 $\frac{2023}{4048}$ B、 $\frac{4046}{2023}$ C、 $\frac{2023}{2024}$ D、 $\frac{2023}{1024}$

查看试题解析
10. 如图1是长方形纸带，将纸带沿EF折叠成图2，再沿BF折叠成图3，若图3中∠CFE=120°，则图1中的∠DEF的度数是（）

A、25° B、30° C、15° D、20°

查看试题解析

二、填空题

11. 化简求值① $\sqrt{16} =$ ；② $\sqrt{{(- 3)}^{2}} =$ ；③ $\sqrt{81}$ 的平方根 $=$ .

查看试题解析
12. 若 $x$ ， $y$ 为实数，且 $| x + 2 y | + \sqrt{y + 1} = 0$ ，则 $y^{x}$ 的值是

查看试题解析
13. 如果角α和角β的两边分别平行，且满足2α＝β+40°，则角α的度数是.

查看试题解析
14. 如图，直线 $A B 、 C D$ 相交于点 $O, O E ⊥ C D, O F$ 平分 $∠ B O D$ ，若 $∠ A O E + ∠ B O F = 66 °$ ，则 $∠ B O C =$ °.

查看试题解析
15. 如图，直线 $A B ∥ C D$ ，点 $E$ 在 $A B$ 上，点 $F$ 在 $C D$ 上，点 $P$ 在 $A B, C D$ 之间， $∠ A E P$ 和 $∠ C F P$ 的角平分线相交于点 $M, ∠ D F P$ 的角平分线交 $E M$ 的反向延长线于点 $N$ ，下列四个结论：
① $∠ E P F = ∠ A E P + ∠ C F P$ ；
② $∠ E P F = 2 ∠ M$ ；
③若 $E P ∥ F N$ ，则 $∠ A E M = ∠ C F M$ ；
④ $∠ M N F + ∠ P E M = 90 ° - ∠ P F M$ ．
其中正确的结论是（填写序号）．

查看试题解析
16. 如图，已知 $A B ∥ C D$ ， $∠ B E C$ 的平分线与 $∠ E C D$ 的平分线的反向延长线相交于点 $P$ ，设 $∠ B =$ $80 °$ ，则 $∠ P =$

查看试题解析

三、解答题

17. 计算．

(1)、 $3 (\sqrt{2} + \sqrt{3}) + | \sqrt{2} - \sqrt{3} | + 2 \sqrt{2}$

(2)、 $\sqrt{2 \frac{1}{4}} - \sqrt[3]{1 - \frac{19}{27}}$

查看试题解析
18. 求下列各式中的 $x$ ．

(1)、 ${(x - 1)}^{2} = 4$

(2)、 $x^{3} - 3 = \frac{3}{8}$

查看试题解析
19. 如图，已知：AD⊥BC于D ， EG⊥BC于G ，若∠E＝∠1.则∠2＝∠3吗？下面是部分推理过程，请你将其补充完整：
∵AD⊥BC于D ， EG⊥BC于G（已知），
∴∠ADC＝_▲_＝90°（_▲_），
∴AD∥EG（_▲_），
∴∠1═∠2（_▲_），
∴∠E＝∠1（已知）
∴∠E＝∠2（_▲_），
∵AD∥EG ，
∴_▲_＝∠3（两直线平行，同位角相等）.
∴_▲_＝_▲_（等量代换）.

查看试题解析
20. 已知：如图1， $∠ 1 + ∠ 2 = 18 0^{°}$ ， $∠ A E F = ∠ H L N$ ， ∠F=36°．

(1)、求证：AB∥CD

(2)、求∠H的度数

查看试题解析
21. 如图，下列网格是边长为1个单位长度的小正方形组成，按照要求完成作图，结果用实线表示.

(1)、如图1， $△ A B C$ 的顶点均在格点上，将 $△ A B C$ 平移得到 $△ D E F$ ， B点的对应点是点E ，画出 $△ D E F$ ，并直接写出 $△ A B C$ 的面积；

(2)、如图2，直线 $L_{^{1}}$ 经过格点A、B ，过点A作直线 $L_{^{2}} ⊥ L_{^{1}}$ ，作直线 $L_{^{3}} ∥ L_{^{2}}$ ，画出直线 $L_{^{2}}$ ， $L_{^{3}}$ ，若继续作 $L_{^{4}} ⊥ L_{^{3}}$ ， $L_{^{5}} ∥ L_{^{4}}$ ， $L_{^{6}} ⊥ L_{^{5}}$ ， $L_{^{7}} ∥ L_{^{6}}$ ……，按此规律，则 $L_{^{9}}$ 与 $L_{^{12}}$ ， $L_{^{100}}$ 与 $L_{^{2023}}$ 的位置关系分别是 $L_{^{9}}$ $L_{^{12}}$ ， $L_{^{100}}$ $L_{^{2023}}$ .

查看试题解析
22. 为实现“绿色江夏·和谐江夏”，江夏区政府准备开发城北一块长为32m，宽为21m的长方形空地．

(1)、方案一：如图1，将这块空地种上草坪，中间修一条弯曲的小路，小路的左边线向右平移1m就是它的右边线．则这块草地的面积为m²；

(2)、方案二：如图2，将这块空地种上草坪，修纵横两条宽1m的小路，则这块草地的面积为m²；

(3)、方案三：修建一个长是宽的1.6倍，面积为432m²的篮球场，若比赛用的篮球场要求长在25m到30m之间，宽在13m到20m之间．这个篮球场能用做比赛吗？并说明理由．

查看试题解析
23. 问题背景：如图 $1$ ，已知 $A B ∥ C D$ ，李老师说 $∠ B$ ， $∠ D$ ， $∠ B E D$ 存在某种数量关系，小明同学经过认真思考，得出了结论，

(1)、请直接写出 $∠ B$ ， $∠ D$ ， $∠ B E D$ 存在的数量关系.

(2)、问题探究：爱动手实践的小芳同学有一块如图 $2$ 七巧板，小芳同学发现 $∠ A$ ， $∠ P$ ， $∠ B$ ， $∠ C$ 存在某种确定的数量关系，请写出你发现的 $∠ A$ ， $∠ P$ ， $∠ B$ ， $∠ C$ 存在的数量关系，并写出证明过程.

(3)、拓展应用：如图 $3$ ，若 $∠ P A Q = 2 ∠ C A Q$ ， $∠ P B Q = 2 ∠ C B Q$ ， $∠ C = α$ ， $∠ Q = β$ ，请直接写出 $∠ P$ 度数（用 $α ， β$ 表示）.

查看试题解析
24. “一带一路”让中国和世界更紧密，“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示，灯A射线从AM开始顺时针旋转至AN便立即回转，灯B射线从BP开始顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视.若灯A转动的速度是每秒2度，灯B转动的速度是每秒1度.假定主道路是平行的，即PQ∥MN，且∠BAM：∠BAN=2：1.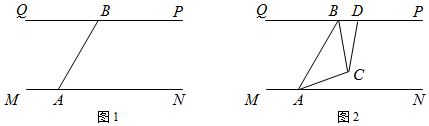

(1)、填空：∠BAN=°；

(2)、若灯B射线先转动30秒，灯A射线才开始转动，在灯B射线到达BQ之前，A灯转动几秒，两灯的光束互相平行？

(3)、如图2，若两灯同时转动，在灯A射线到达AN之前.若射出的光束交于点C，过C作∠ACD交PQ于点D，且∠ACD=120°，则在转动过程中，请探究∠BAC与∠BCD的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请说明理由.

查看试题解析