广西壮族自治区桂林市2023-2024学年八年级下学期数学期中试题

试卷更新日期：2024-05-14 类型：期中考试

进入出卷网下载

一、单选题（每题3分，共36分）

1. 2023年10月8日晚，伴随圣火缓缓熄灭，杭州第19届亚运会圆满闭幕，亚运是体育盛会，也是文化旅游的盛会．下列与杭州亚运会有关的图案中，属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列长度的三条线段首尾相连能组成直角三角形的是（）

A、4，5，6 B、1，2，3 C、2，3，4 D、5，12，13

查看试题解析
3. 直角三角形的一个锐角是 $70 °$ ，则它的另一个锐角是（）

A、 $20 °$ B、 $70 °$ C、 $110 °$ D、 $20 °$ 或 $70 °$

查看试题解析
4. 在▱ABCD中，若∠A：∠B＝1：2，则∠A的度数为（）

A、30° B、60° C、120° D、150°

查看试题解析
5. 若菱形的两条对角线长分别为10和24，则菱形的面积为（）

A、13 B、26 C、120 D、240

查看试题解析
6. 图1是三角形空地，计划用栅栏分成两部分种植不同的植物如图2，则栅栏AB的长度是（）

A、2m B、3m C、4m D、1m

查看试题解析
7. 已知四边形ABCD是平行四边形，下列结论中不一定成立的是（）

A、AC=BD B、AB=CD C、当AC⊥BD时，它是菱形 D、当∠ABC＝90°时，它是矩形

查看试题解析
8. 菱形、矩形、正方形都具有的性质是（）

A、两组对边分别平行且相等 B、对角线相等 C、四条边相等，四个角相等 D、对角线互相垂直

查看试题解析
9. 如图，三位同学分别站在一个直角三角形的三个直角顶点处做投圈游戏，目标物放在斜边 $A B$ 的中点 $E$ 处，已知 $A B = 6 m$ ，则点 $C$ 到点 $E$ 的距离是（）

A、 $6 m$ B、 $2.5 m$ C、 $4 m$ D、 $3 m$

查看试题解析
10. 已知，如图，B、C、E三点在同一条直线上，AC=CD，∠B=∠E=90°，AB=CE，则不正确的结论是（）

A、∠A与∠D互为余角 B、∠A=∠2 C、△ABC≌△CED D、∠1=∠2

查看试题解析
11. 小明用四根长度相同的木条制作了能够活动的菱形学具，他先活动学具成为图1所示菱形，并测得∠B＝60°，对角线AC＝20cm ，接着活动学具成为图2所示正方形，则图2中对角线AC的长为（）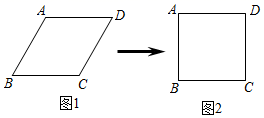

A、20cm B、30cm C、40cm D、20 $\sqrt{2}$ cm

查看试题解析
12. 如图，点 $O$ ， $B$ 在数轴上所表示的数分别为0，3， $C B ⊥ O B$ 于点 $B$ ， $B C = 2$ ，以点 $O$ 为圆心， $O C$ 长为半径画弧，交数轴于点 $A$ ，若点 $A$ 所表示的数为 $a$ ，则 $a$ 的值为（）

A、 $\sqrt{13}$ B、 $- \sqrt{13}$ C、 $\sqrt{5}$ D、 $- \sqrt{5}$

查看试题解析

二、填空题（每题2分，共12分）

13. 已知直角三角形的两直角边长分别为2和4，则斜边长为．

查看试题解析
14. 一个正多边形的内角和等于它的外角和的3倍，则这个正多边形是正边形．

查看试题解析
15. 如图， $∠ A C B = ∠ D B C = 90 °$ ，要根据“ $H L$ ”证明 $R t △ A B C ≌ △ D C B$ ，应添加的直接条件是.

查看试题解析
16. 如图，矩形ABCD的两条对角线相交于点O，∠AOB=60°，AB=2，则AC=

查看试题解析
17. 如图，沿 $A C$ 方向开山修建一条公路，为了加快施工进度，要在小山的另一边寻找点E同时施工（点A、B、C、E在同一条直线上），从 $A C$ 上的一点B取 $∠ A B D = 150 °$ ，沿 $B D$ 的方向前进，取 $∠ B D E = 60 °$ ，测得 $B D = 500 m$ ， $B C = 80 m$ ，并且 $A C$ 、 $B D$ 和 $D E$ 在同一平面内，那么公路 $C E$ 段的长度为．

查看试题解析
18.
如图，正方形ABCD中，AB=4，E是BC的中点，点P是对角线AC上一动点，则PE+PB的最小值为．

查看试题解析

三、解答题（共72分）

19.
如图，∠A=∠D=90°，AB=DE，BF=EC．求证：Rt△ABC≌Rt△DEF．

查看试题解析
20. 已知：如图，在平行四边形 $A B C D$ 中，E、F是对角线 $A C$ 上的两点，且 $A F = C E$ ．求证： $D E = B F$ ．

查看试题解析
21. 如图，四边形 $A B C D$ 是矩形，过A作 $A E ∥ B D$ 交 $C B$ 的延长线于点E ，证明： $A E = A C$ ．

查看试题解析
22.
在△ABC中，CD⊥AB于D，CE是∠ACB的平分线，∠A=20°，∠B=60°．求∠BCD和∠ECD的度数．

查看试题解析
23. 如图，已知 CD⊥AB 于点 D，BE⊥AC 于点 E，BE，CD 交于点 O，且 OB=OC．
求证：AO平分∠BAC．

查看试题解析
24. 有一矩形纸片，按如图方式折叠，使点 $B$ 与点 $D$ 重合，折痕为 $E F$ ；

(1)、求证： $△ D E F$ 是等腰三角形；

(2)、若 $A D = 3$ ， $A B = 9$ ，求 $D E$ 的长．

查看试题解析
25. 阅读材料，并完成相应任务．
2000多年来，人们对勾股定理的证明颇感兴趣，不但因为这个定理重要、基本，还因为这个定理贴近人们的生活实际，所以很多人都探讨、研究它的证明，新的证法不断出现，下面的图形是传说中毕达哥拉斯的证明图形：
证明：①在图1中，∵ $S_{大正方形} = {(a + b)}^{2}$ ，
$S_{大正方形} = 4$ 个直角三角形的面积+两个正方形的面积，
$= 4 \times$     ▲     $+$     ▲     $+$     ▲     ，
②在图2中，
∵ $S_{大正方形} = {(a + b)}^{2}$ ，
$S_{大正方形} = 4$ 个直角三角形面积 $+$ 小正方形的面积，
$= 4 \times$     ▲     $+$     ▲     ．
∴    ▲     $=$     ▲     ，
整理得： $2 a b + a^{2} + b^{2} = 2 a b + c^{2}$ ，
∴    ▲     ．
任务：

(1)、将材料中的空缺部分补充完整；

(2)、如图3，在 $△ A B C$ 中， $∠ A = 60 °$ ， $∠ A C B = 75 °$ ， $C D ⊥ A B$ ， $A C = 4$ ，求 $B C$ 的长．

查看试题解析
26. 如图， $△ A B C$ 中，点O为 $A C$ 边上的一个动点，过点O作直线 $M N ∥ B C$ ，设 $M N$ 交 $∠ B C A$ 的外角平分线 $C E$ 于点F ，交 $∠ A C B$ 内角平分线 $C E$ 于E ．

(1)、求证： $E O = F O$ ；

(2)、当点O运动到何处时，四边形 $A E C F$ 是矩形？并证明你的结论；

(3)、若 $A C$ 边上存在点O ，使四边形 $A E C F$ 是正方形，猜想 $△ A B C$ 的形状并证明你的结论．

查看试题解析