云南省楚雄彝族自治州2023-2024学年七年级下学期数学期中试题

试卷更新日期：2024-05-14 类型：期中考试

进入出卷网下载

一、选择题（本大题共15小题，每小题只有一个正确选项，每小题2分，共30分）

1. 下列图形中∠1与∠2互为对顶角的是（）

A、 B、 C、 D、

查看试题解析
2. 实数4的算术平方根是（）

A、－2 B、2 C、±2 D、±4

查看试题解析
3. 如图，直线 $c$ 与直线 $a 、 b$ 都相交．若 $a ∥ b ， ∠ 1 = 35 °$ ，则 $∠ 2 =$ （）

A、 $145 °$ B、 $65 °$ C、 $55 °$ D、 $35 °$

查看试题解析
4. 平面直角坐标系中，点 $(3, - 2)$ 在（）象限

A、第一 B、第二 C、第三 D、第四

查看试题解析
5. 下列实数中是无理数的是（）

A、 $\sqrt{9}$ B、 $\sqrt{5}$ C、 $\sqrt[3]{8}$ D、 $0.333 ⋯$

查看试题解析
6. 计算： $| 1 - \sqrt{2} |$ ＝（）

A、 $1 - \sqrt{2}$ B、 $\sqrt{2} - 1$ C、 $1 + \sqrt{2}$ D、1

查看试题解析
7. 下列运算中，正确的是（）

A、 $\sqrt[3]{- 1} = 1$ B、 $\sqrt{16} = \pm 4$ C、 $- \sqrt{(- 2)^{2}} = - 2$ D、 $\sqrt{2^{2}} = 2 \sqrt{2}$

查看试题解析
8. 下列命题中，真命题是（）

A、若 $a ∥ b$ ， $c ∥ d$ ，则 $a ∥ c$ B、若 $a ⊥ b ， b ∥ c$ ，则 $a ⊥ c$ C、若两直线被第三条直线所截，则内错角相等 D、若两条平行线被第三条直线所截，则一对同旁内角的平分线互相平行

查看试题解析
9. 如图，下列条件中，能判断AB∥CD的是（）

A、∠A＝∠CBE B、∠A＝∠C C、∠C＝∠CBE D、∠C＋∠D＝180°

查看试题解析
10. 将点 $P (1 ， - 2)$ 向右平移3个单位长度得到点 $P^{'}$ ，则点 $P^{'}$ 的坐标是（）

A、 $(4 ， - 2)$ B、 $(4 ， - 1)$ C、 $(4 ， 0)$ D、 $(- 2 ， - 2)$

查看试题解析
11. 如图，直线 $B C$ 与 $D E$ 相交于点O ， $∠ A O B = 90 °, ∠ A O E = 116 °$ ，则 $∠ C O E$ 的度数为（）

A、 $154 °$ B、 $116 °$ C、 $64 °$ D、 $26 °$

查看试题解析
12. 按一定规律排列的单项式： $a ， \sqrt{2} a^{2} ， \sqrt{3} a^{3} ， \sqrt{4} a^{4} ， \sqrt{5} a^{5} ， ⋯$ ，第 $n$ 个单项式是（）

A、 $\sqrt{n}$ B、 $\sqrt{n - 1} a^{n - 1}$ C、 $\sqrt{n} a^{n}$ D、 $\sqrt{n} a^{n - 1}$

查看试题解析
13.
如图，要把河中的水引到水池A中，应在河岸B处（AB⊥CD）开始挖渠才能使水渠的长度最短，这样做依据的几何学原理是（　　）

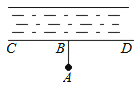A、两点之间线段最短 B、点到直线的距离 C、两点确定一条直线 D、垂线段最短

查看试题解析
14. 实数a、b在数轴上的位置如图所示，则化简 $\sqrt{(a - b)^{2}}$ 的结果是（）

A、 $a - b$ B、 $b - a$ C、0 D、 $a + b$

查看试题解析
15. 如图，已知 $∠ 3 = ∠ 4$ ，下列结论正确的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 2 = ∠ 3$ C、 $∠ B = ∠ 5$ D、 $∠ D = ∠ 5$

查看试题解析

二、填空题（本大题共4小题，每小题2分，共8分）

16. 4的平方根是

查看试题解析
17. 如图，直线 $a 、 b$ 被直线 $c$ 所截， $a ∥ b$ ，已知 $∠ 2 = 82 °$ ，则 $∠ 1 =$ ．

查看试题解析
18. 将命题“对顶角相等”用“如果…那么…”的形式可以改写为．

查看试题解析
19. 中国象棋是中华民族的文化瑰宝，因趣味性强，深受大众喜爱.如图，若在象棋棋盘上建立平面直角坐标系，使“帅”位于点 $(0 ， ﹣ 2)$ ，“马”位于点 $(4 ， ﹣ 2)$ ，则“兵”位于点.

查看试题解析

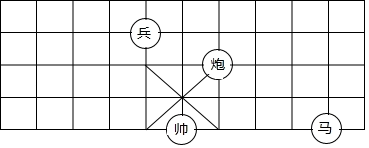
三、解答题（本大共8小题，共62分）

20. 计算： $\sqrt{16} - {(- 1)}^{2024} + \sqrt[3]{- 8} + \sqrt{0}$ ．

查看试题解析
21. 计算： $\sqrt{{(- 3)}^{2}} - \sqrt{2} (\sqrt{2} - 1)$ ．

查看试题解析
22. 如图，已知火车站的坐标为 $(2 ， 1)$ ，文化宫的坐标为 $(- 1 ， 2)$ ．

(1)、请你根据题目条件，画出平面直角坐标系；

(2)、写出体育场、市场、超市、医院的坐标．

查看试题解析
23. 如图：已知 $∠ B = ∠ B G D ， ∠ C G B = ∠ F$ ，求证： $∠ B + ∠ F = 180 °$ ．
请你认真完成下面的填空．
证明：∵ $∠ B = ∠ B G D$ （    ）
∴ $A B ∥ C D$ （    ）
∵ $∠ C G B = ∠ F$ （    ）
∴ $C D ∥ E F$ （    ）
∴ $A B ∥ E F$ （    ）
∴ $∠ B + ∠ F = 180 °$ （    ）．

查看试题解析
24. 已知一个正数a的两个平方根分别是x＋3和2x－15，求x和a的值．

查看试题解析
25. 如图，在平面直角坐标系中， $△ A B C$ 如图所示，将 $△ A B C$ 向上平移4个单位长度，再向左平移3个单位长度，得到 $△ A_{1} B_{1} C_{1}$ ．

(1)、直接写出 $△ A B C$ 三个顶点的坐标；

(2)、 $B C$ 与 $B_{1} C_{1}$ 之间的位置关系：；

(3)、画出 $△ A_{1} B_{1} C_{1}$ ，并写出 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 三点的坐标．

查看试题解析
26. 如图所示，已知 $A E ⊥ C B ， G F ⊥ C B$ ， $∠ 1 = ∠ 2$ ．

(1)、求证： $A B ∥ C D$ ；

(2)、若 $∠ C = 25 ° ， ∠ D - ∠ 4 = 15 °$ ，求 $∠ D$ 的度数．

查看试题解析
27. 如图， $A (- 1, 0)$ ， $C (1, 4)$ ，点 $B$ 在 $x$ 轴上，且 $A B = 3$ ．

(1)、求点B的坐标；

(2)、求 $△ A B C$ 的面积；

(3)、在y轴上是否存在点P ，使以A ， B ， P三点为顶点的三角形的面积为15?若存在，请求出点P的坐标；若不存在，请说明理由．

查看试题解析