重庆市丰都县融智教育集团2023-2024学年八年级下学期数学期中试题
试卷更新日期:2024-05-14 类型:期中考试
一、选择题(本大题10个小题,每小题4分,共40分,在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑)
-
1. 下列各组数中,能构成直角三角形的是( )A、4,5,6 B、1,1, C、6,8,11 D、5,12,232. 下列计算正确的是( )A、 B、 C、 D、3. 如图,在中, , , 于点E , 则等于( )
 A、20° B、110° C、70° D、50°4. 估计的值应在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间5. 下列命题中,真命题是( )A、对角线相等的四边形是矩形 B、一组对边平行,另一组对边相等的四边形是平行四边形 C、对角线互相垂直平分的四边形是菱形 D、一组邻边相等,并且有一个内角为直角的四边形是正方形6. 如图,在菱形中,对角线、交于点 , 点是的中点,若 , , 则菱形的面积是( )
A、20° B、110° C、70° D、50°4. 估计的值应在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间5. 下列命题中,真命题是( )A、对角线相等的四边形是矩形 B、一组对边平行,另一组对边相等的四边形是平行四边形 C、对角线互相垂直平分的四边形是菱形 D、一组邻边相等,并且有一个内角为直角的四边形是正方形6. 如图,在菱形中,对角线、交于点 , 点是的中点,若 , , 则菱形的面积是( ) A、48 B、36 C、24 D、187. 如图,在矩形中, , , 对角线 , 相交于点O,点E,F分别是 , 的中点,连接 , 则的周长为( )
A、48 B、36 C、24 D、187. 如图,在矩形中, , , 对角线 , 相交于点O,点E,F分别是 , 的中点,连接 , 则的周长为( ) A、6 B、7 C、8 D、98. 勾股定理是我国古代的伟大数学发明之一.如图,以的各边向外作正方形,得到三块正方形纸片,再把较小的两张正方形纸片放入最大的正方形中,重叠部分的面积记作 , 左下不重叠部分的面积记作 , 若 , 则的值是( )
A、6 B、7 C、8 D、98. 勾股定理是我国古代的伟大数学发明之一.如图,以的各边向外作正方形,得到三块正方形纸片,再把较小的两张正方形纸片放入最大的正方形中,重叠部分的面积记作 , 左下不重叠部分的面积记作 , 若 , 则的值是( ) A、1 B、 C、2 D、9. 如图:正方形中,点E、F分别是、边上的点,连接 , 交于点N , 的角平分线交于M , 过点M作分别交于点H , 交于点Q , 连接 , 若 , , 则用含a的代数式表示为( )
A、1 B、 C、2 D、9. 如图:正方形中,点E、F分别是、边上的点,连接 , 交于点N , 的角平分线交于M , 过点M作分别交于点H , 交于点Q , 连接 , 若 , , 则用含a的代数式表示为( ) A、 B、 C、 D、10. 对于从左到右依次排列的三个实数a、b、c , 在a与b之间、b与c之间只添加一个四则运算符号“+”、“-”、“×”、“÷”组成算式(不再添加改变运算顺序的括号),并按四则运算法则计算结果,称为对实数a、b、c进行“四则操作”,例如:对实数4、5、6的“四则操作”可以是: , 也可以是;对实数2, , 的一种“四则操作”可以是 . 给出下列说法:
A、 B、 C、 D、10. 对于从左到右依次排列的三个实数a、b、c , 在a与b之间、b与c之间只添加一个四则运算符号“+”、“-”、“×”、“÷”组成算式(不再添加改变运算顺序的括号),并按四则运算法则计算结果,称为对实数a、b、c进行“四则操作”,例如:对实数4、5、6的“四则操作”可以是: , 也可以是;对实数2, , 的一种“四则操作”可以是 . 给出下列说法:① 对实数1、4、2进行“四则操作”后的结果可能是6;
② 对于实数2、、3进行.“四则操作”后,所有的结果中最大的是21;
③ 对实数x、x、2进行“四则操作”后的结果为6,则x的值共有16个;
其中正确的个数是( )
A、0 B、1 C、2 D、3二、填空题(本大题4个小题,每小题8分,共32分,请将每小题的答案直接填在答题卡中对应的横线上)
-
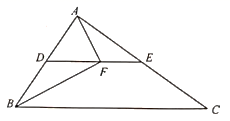
11. 若式子有意义,则x的取值范围是 .12. 如图所示, 为 的中位线,点F在 上,且 ,若 则 的长为.
 13. 我同古代有这样一道数学问题:今有一竖直着的木柱,在木柱的上端系有绳索,绳索从木柱的上端顺木柱下垂后堆在地面的部分有三尺(绳索比木柱长尺),牵着绳索退行,在距木柱底部尺处时绳索用尽,则木柱长为尺.14. 已知实数 , , 在数轴上对应点的位置如图所示,化简 .
13. 我同古代有这样一道数学问题:今有一竖直着的木柱,在木柱的上端系有绳索,绳索从木柱的上端顺木柱下垂后堆在地面的部分有三尺(绳索比木柱长尺),牵着绳索退行,在距木柱底部尺处时绳索用尽,则木柱长为尺.14. 已知实数 , , 在数轴上对应点的位置如图所示,化简 . 15. 如图,在菱形中,对角线 , 交于点 , 于点 , , , 则的长为
15. 如图,在菱形中,对角线 , 交于点 , 于点 , , , 则的长为 16. 如图,在中, , , , 是边的中点,连接 , 将沿翻折,得到 , 连接 , 则点到的距离为 .
16. 如图,在中, , , , 是边的中点,连接 , 将沿翻折,得到 , 连接 , 则点到的距离为 . 17. 如果关于x的不等式组至少有两个整数解,且关于y的分式方程的解
17. 如果关于x的不等式组至少有两个整数解,且关于y的分式方程的解为正整数,则符合条件的所有整数m的和为 .
18. 对于任意一个四位数 , 若它的千位数字与百位数字的和比十位数字与个位数字的和大 , 则称这个四位数根为“差双数”,记为的各个数位上的数字之和.例如: , , 是“差双数”, ; , , 不是“差双数”.若与都是“差双数”,且 , 则“差双数”是;已知M , N均为“差双数”,其中 , , , , , , , , , , 是整数 , 已知能被整除,且为整数,则满足条件的所有的的值之和为 .三、解答题(本大题共8小题,19题8分,20-26题每题10分,共78分,解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上)
-
19. 计算:(1)、(2)、20. 如图,在中,点E , F分别在 , 的延长线上,且 , 与交于点O . 求证: .
 21. 如图,在四边形中,∥ , , 对角线、交于点 , 平分 , 过点作交延长线于点 , 连接 .
21. 如图,在四边形中,∥ , , 对角线、交于点 , 平分 , 过点作交延长线于点 , 连接 . (1)、求证:四边形是菱形;(2)、若 , , 求四边形的面积.22. 如图,四边形是平行四边形,于E .
(1)、求证:四边形是菱形;(2)、若 , , 求四边形的面积.22. 如图,四边形是平行四边形,于E . (1)、尺规作图:过点C作于点F , 连接 . (要求:保留作图痕迹,不写作法,不下结论)(2)、求证: . 将下面的过程补充完整.
(1)、尺规作图:过点C作于点F , 连接 . (要求:保留作图痕迹,不写作法,不下结论)(2)、求证: . 将下面的过程补充完整.证明:∵ , ,
∴ ▲ , ;
∵四边形ABCD是平行四边形,
∴ ▲ , ,
∴ ▲ .
在和中,
,
∴ ,
∴ ▲ ,
又∵ ,
∴四边形是 ▲ ;( )(填推理的依据)
∴ .
23. 阅读理解:我们把称作二阶行列式,规定它的运算法则为 , 例如 , 请根据阅读理解解答下列各题:(1)、;(2)、计算:;(3)、已知实数a , b满足行列式 , 则代数式的值.24. 小明和小红相约周末游览合川钓鱼城,如图,为同一平面内的五个景点.已知景点位于景点的东南方向米处,景点位于景点的北偏东方向米处,景点位于景点的北偏东方向,若景点与景点 , 都位于东西方向,且景点在同一直线上. (1)、求景点与景点之间的距离.(结果保留根号)(2)、小明从景点出发,从到到 , 小红从景点出发,从到到 , 两人在各景点处停留的时间忽略不计.已知两人同时出发且速度相同,请通过计算说明谁先到达景点 . (参考数据:)25. 如图,正方形中,E是边上一点,连接 , 以为边在右侧作正方形 , 连接 , 交于点N , 连接 . 过点F作交的延长线于点G .
(1)、求景点与景点之间的距离.(结果保留根号)(2)、小明从景点出发,从到到 , 小红从景点出发,从到到 , 两人在各景点处停留的时间忽略不计.已知两人同时出发且速度相同,请通过计算说明谁先到达景点 . (参考数据:)25. 如图,正方形中,E是边上一点,连接 , 以为边在右侧作正方形 , 连接 , 交于点N , 连接 . 过点F作交的延长线于点G . (1)、求证:;(2)、求证: .26. 在中, , , D为上任意一点,E为上任意一点.
(1)、求证:;(2)、求证: .26. 在中, , , D为上任意一点,E为上任意一点. (1)、如图1,连接 , 若 , , 求的长.(2)、如图2,若点D为中点,连接 , 点F为上任意一点,连接并延长交于点M , 将线段绕点E顺时针旋转得到线段 , 连接 , 点N在上,且 , 求证: .(3)、如图3,点D为中点,连接 , 点F为的中点,连接、 , 将线段绕点E顺时针旋转得到线段 , 连接 , H为直线上一动点,连接 , 将沿翻折至所在平面内,得到 , 连接 , 直接写出线段的长度的最大值.
(1)、如图1,连接 , 若 , , 求的长.(2)、如图2,若点D为中点,连接 , 点F为上任意一点,连接并延长交于点M , 将线段绕点E顺时针旋转得到线段 , 连接 , 点N在上,且 , 求证: .(3)、如图3,点D为中点,连接 , 点F为的中点,连接、 , 将线段绕点E顺时针旋转得到线段 , 连接 , H为直线上一动点,连接 , 将沿翻折至所在平面内,得到 , 连接 , 直接写出线段的长度的最大值.