浙江省杭州市萧山区城区八校2023-2024学年八年级下学期数学期中考试试卷

试卷更新日期：2024-05-14 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 下列计算正确的是（　　）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $3 \sqrt{2} - \sqrt{2} = 3$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{3.6} = 0.6$

查看试题解析
2. 下列图形中，属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 用配方法解一元二次方程x²+2x﹣3＝0，配方后得到的方程是（）

A、（x﹣1）²＝4 B、（x+1）²＝4 C、（x+2）²＝1 D、（x﹣2）²＝1

查看试题解析
4. 王老师对甲、乙两人五次数学成绩进行统计，两人平均成绩均为90分，方差S_甲²=12，S_乙²=51，则下列说法正确的是（　　）

A、甲、乙两位同学的成绩一样稳定 B、乙同学的成绩更稳定 C、甲同学的成绩更稳定 D、不能确定

查看试题解析
5. 在平面直角坐标系中，点P $(\sqrt{3}, - \sqrt{13})$ 到原点的距离等于（　　）

A、6 B、5 C、4 D、3

查看试题解析
6. 无论x取任何实数，代数式 $\sqrt{x^{2} - 6 x + m}$ 都有意义，则m的取值范围是（）

A、 $m \geq 9$ B、 $m \leq 9$ C、 $m < 9$ D、 $m > 9$

查看试题解析
7. 流行性感冒传染迅速，若有一人感染，经过两轮传染后共有100人患病，设每轮传染中平均一人传染了x人，可列出的方程是（　　）

A、 ${(x + 1)}^{2} = 100$ B、 $1 + {(x + 1)}^{2} = 100$ C、 $x + x (1 + x) = 100$ D、 $1 + x + x^{2} = 100$

查看试题解析
8. 已知：一组数据x₁ ， x₂ ， x₃ ， x₄ ， x₅的平均数是2，方差是 $\frac{1}{3}$ ，那么另一组数据3x₁﹣2，3x₂﹣2，3x₃﹣2，3x₄﹣2，3x₅﹣2的平均数和方差分别是（）

A、2， $\frac{1}{3}$ B、2，1 C、4， $\frac{2}{3}$ D、4，3

查看试题解析
9. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，下列说法：
$①$ 若 $a + c = b$ ，则 $b^{2} - 4 a c \geq 0$ ；
$②$ 若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ 必有两个不相等的实根；
$③$ 若 $x = c$ 是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；
其中正确的是（　　）

A、 $①$ B、 $① ③$ C、 $① ②$ D、 $② ③$

查看试题解析
10. 如图，四边形 $A B C D$ 是平行四边形，连接 $B D$ ，过点A作 $A M ⊥ B C$ 于点M，交 $B D$ 于点E，连接 $C E$ ，若 $E A = E C$ ，点M为 $B C$ 的中点， $A B = 2$ ，则 $A E$ 的值为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{2 \sqrt{3}}{3}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\sqrt{2}$

查看试题解析

二、填空题（每小题4分，共24分）

11. 若二次根式 $\sqrt{x + 4}$ 有意义.则x的取值范围是.

查看试题解析
12. 八边形的内角和是度，外角和是度．

查看试题解析
13. 某学生数学课堂表现为90分，平时作业为92分，期末考试为85分，若这三项成绩分别按30%，30%，40%的比例记入总评成绩，则该生数学总评成绩是分．

查看试题解析
14. 已知关于x的一元二次方程 $x^{2} - 2 a x + 3 a = 0$ 的一个根是2，则另一个根是．

查看试题解析
15. 设实数 $\sqrt{5}$ 的整数部分为 $a$ ，小数部分为 $b$ ，则 $(2 a + b) (2 a - b) =$ ．

查看试题解析
16. 已知点D与点 $A (4, 0)$ ， $B (0, 6)$ ， $C (a, - a)$ 是平行四边形的四个顶点，则 $C D$ 长的最小值为．

查看试题解析

三、解答题（共66分）

17. 计算

(1)、 $| - 3 | + \sqrt{8} - \sqrt{2}$ ；

(2)、 $\sqrt{{(- 3)}^{2}} - \sqrt{24} \div \sqrt{2} + \sqrt{18}$ ．

查看试题解析
18. 解方程

(1)、 $x^{2} - 4 x - 2 = 0$

(2)、 $6 x^{2} - 2 x = 0$

查看试题解析
19. 如图所示，有一张边长为 $6 \sqrt{3} c m$ 的正方形纸板，现将该纸板的四个角剪掉，制作成一个有底无盖的长方体盒子，剪掉的四个角是面积相等的小正方形，此小正方形的边长为 $\sqrt{3} c m$ ，求：

(1)、长方体盒子的底面积；

(2)、长方体盒子的体积．

查看试题解析
20. 甲、乙两人在5次打靶测试中命中的环数如下：
甲：8，8，7，8，9
乙：5，9，7，10，9

(1)、请求出下表中a ， b ， c的值

平均数
众数
中位数
方差
甲
8
$a$
8
0.4
乙
$b$
9
$c$
3.2

(2)、如果乙再射击1次，命中8环，那么乙的射击成绩的方差．（填“变大”、“变小”或“不变”）

查看试题解析
21. 如图，在▱ABCD中，点O是对角线AC、BD的交点，EF过点O且垂直于AD．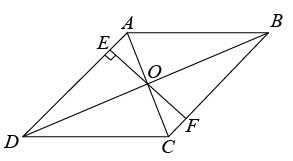

(1)、求证：OE＝OF；

(2)、若S_▱ABCD＝63，OE＝3.5，求AD的长．

查看试题解析
22. 已知关于x的方程 $x^{2} - (k + 3) x + 3 k = 0$ .

(1)、求证：无论k取任何实数，该方程总有实数根；

(2)、若等腰三角形的三边长分别为a ， b ， c ，其中 $a = 1$ ，并且b ， c恰好是此方程的两个实数根，求此三角形的周长.

查看试题解析
23. 某商场以每件 $280$ 元的价格购进一批商品，当每件商品售价为 $360$ 元时，每月可售出 $60$ 件．为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价 $1$ 元，那么商场每月就可以多售出 $5$ 件．

(1)、降价前商场每月销售该商品的利润是多少元？

(2)、要使商场每月销售这种商品的利润达到 $7200$ 元，且更有利于减少库存，则每件商品应降价多少元？

(3)、该商场 $1$ 月份销售量为 $60$ 件， $2$ 月和 $3$ 月的月平均增长率为 $x$ ，若前三个月的总销量为 $285$ 件，求该季度的总利润．

查看试题解析
24. 如图，平行四边形ABCD中∠A＝60°，AB＝6cm，AD＝3cm，点E以1cm/s的速度从点A出发沿A一B一C向点C运动，同时点F以1cm/s的速度从点A出发沿A一D一C向点C运动，当一个点到达终点时，另一个点也停止运动，设运动的时间为t（s）.

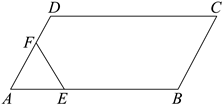(1)、求平行四边形ABCD的面积；

(2)、求当t＝2s时，求△AEF的面积；

(3)、当△AEF的面积为平行四边形ABCD的面积的 $\frac{1}{3}$ 时，求t的值.

查看试题解析

	平均数	众数	中位数	方差
甲	8	$a$	8	0.4
乙	$b$	9	$c$	3.2