湖北省武汉市江岸区2023-2024学年七年级下学期数学期中试题

试卷更新日期：2024-05-14 类型：期中考试

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分）

1. 下列四个数中，属于无理数的是（）

A、0 B、1.33 C、 $\frac{1}{2}$ D、 $\sqrt{3}$

查看试题解析
2. 如图，小明用手盖住的点的坐标可能为（）

A、 $(3 ， 2)$ B、 $(- 3 ， 2)$ C、 $(3 ， - 2)$ D、 $(- 3 ， - 2)$

查看试题解析
3. 在平面直角坐标系中，点 $A (- 2, 3)$ 向右平移3个单位长度，再向下平移5个单位长度后对应点B ，则点B的坐标是（）

A、 $(1, - 2)$ B、 $(1, 8)$ C、 $(- 5, 2)$ D、 $(- 5, - 2)$

查看试题解析
4. 如图，在 $△ A B C$ 中，点D，E，F分别在边 $B C$ ， $A B$ ， $A C$ 上，下列不能判定 $D E ∥ A C$ 的条件是（）

A、 $∠ 3 = ∠ C$ B、 $∠ 1 + ∠ 4 = 180 °$ C、 $∠ 1 = ∠ A F E$ D、 $∠ 1 + ∠ 2 = 180 °$

查看试题解析
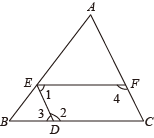5. 若 $2 m - 4$ 与 $3 m - 1$ 是同一个数的两个不同的平方根，则m的值（）

A、 $- 3$ B、1 C、 $- 3$ 或1 D、 $- 1$

查看试题解析
6. 下列命题中是真命题的是（）

A、相等的角是对顶角 B、平方根等于本身的数有 $\pm 1$ 和0 C、垂线段最短 D、两点之间直线最短

查看试题解析
7. 黄金分割数 $\frac{\sqrt{5} - 1}{2}$ 是一个很奇妙的数，大量应用于艺术、建筑和统计决策等方面，请你估算 $\sqrt{5}$ ﹣1的值（）

A、在1.1和1.2之间 B、在1.2和1.3之间 C、在1.3和1.4之间 D、在1.4和1.5之间

查看试题解析
8. 如图，小明从A出发沿北偏东60°方向行走至B处，又沿北偏西20°方向行走至C处，此时需把方向调整到与出发时一致，则方向的调整应是（）

A、右转40° B、右转60° C、右转80° D、右转100°

查看试题解析
9. 如图，在平面直角坐标系中，三角形 $A_{1} A_{2} A_{3}$ ，三角形 $A_{3} A_{4} A_{5}$ ，三角形 $A_{5} A_{6} A_{7}$ ， ……，是斜边在x轴上，斜边长分别为2，4，6……的等腰直角三角形．若三角形 $A_{1} A_{2} A_{3}$ 的顶点坐标分别为 $A_{1} (2, 0)$ ， $A_{2} (1, - 1)$ ， $A_{3} (0, 0)$ ，则依图中所示规律， $A_{2027}$ 的坐标为（）

A、 $(- 1012, 0)$ B、 $(1012, 0)$ C、 $(1015, 0)$ D、 $(- 1015, 0)$

查看试题解析
10. 在平面直角坐标系中，已知点 $A (m - 4, m + 2)$ ， $B (m - 4, m)$ ， $C (m, 0)$ ， $D (2, 0)$ ，已知三角形 $A B D$ 的面积是三角形 $A B C$ 面积的2倍，则m的值为（）

A、 $- 14$ B、2 C、 $- 14$ 或2 D、14或 $- 2$

查看试题解析

二、填空题（共6小题，每小题3分，共18分）

11. 计算： $\sqrt[3]{- 1} =$ ， $\sqrt{{(- 2)}^{2}} =$ ， $\sqrt{4} =$ ．

查看试题解析
12. 如图，直线 $A B ， C D$ 相交于点O ， $E O ⊥ C D$ 于点O ．若 $∠ B O D ： ∠ B O C = 2 ： 7$ ，则 $∠ A O E$ 的度数为．

查看试题解析
13. 在平面直角坐标系中，点 $A (a, - 2)$ ， $B (3, a - 1)$ ，且直线 $A B ∥ x$ 轴，则 $a$ 的值是．

查看试题解析
14. 如图，圆的直径为1个单位长度，该圆上的点 $A$ 与数轴上表示 $- 1$ 的点重合，将圆沿数轴负方向滚动一周，点 $A$ 到达点 $A^{'}$ 的位置，则点 $A^{'}$ 表示的数是．

查看试题解析
15. 如图，将长方形纸片ABCD沿EF折叠（折线EF交AD于E ，交BC于F ，点C、D的落点分别是 $C^{'}$ 、 $D^{'}$ ， $E D^{'}$ 交BC于G ，再将四边形 $C^{'} D^{'} G F$ 沿FG折叠，点 $C^{'}$ 、 $D^{'}$ 的落点分别是 $C^{″}$ 、 $D^{″}$ ， $G D^{″}$ 交EF于H ，下列四个结论：① $∠ G E F = ∠ G F E$ ；② $2 ∠ E F C = ∠ E G C + 180 °$ ；③ $∠ E G D^{″} = 2 ∠ E F G$ ；④ $∠ E H G = 3 ∠ E F B$ ．其中正确的结论是（填写序号）．

查看试题解析
16. 在平面直角坐标系xOy中，对于不同的两点M ， N ，若点M到x轴，y轴的距离的较大值等于点N到x轴，y轴的距离的较大值，则称点M ， N互为“最距等点”．例如：点 $(3, - 4)$ ， $(4, - 2)$ 互为“最距等点”；点 $(3, - 3)$ ， $(- 3, 0)$ 互为“最距等点”．已知点 $P (2 - n, - 2 n + 1)$ 与点 $Q (n + 1, 2 n - 3)$ 互为“最距等点”，则n的值为．

查看试题解析

三、解答题（共8小题，共72分）

17. 计算：

(1)、 $\sqrt{25} - \sqrt[3]{8} + 2 \sqrt{\frac{1}{4}}$

(2)、 $| 2 - \sqrt{2} | + \sqrt{2} (\sqrt{2} - \frac{1}{\sqrt{2}})$

查看试题解析
18. 解方程：

(1)、 ${(x - 1)}^{2} = 9$

(2)、 ${(x + 1)}^{3} = 27$

查看试题解析
19. 如图， $E F ⊥ A C$ 于点 $F$ ， $D B ⊥ A C$ 于点 $M$ ， $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ C$ ，请问 $A B$ 与 $M N$ 平行吗？请完成下面的推理过程，并在括号内写出推理依据．
解： $A B ∥ M N$ ．理由如下：
因为 $E F ⊥ A C$ ， $D B ⊥ A C$ ，（已知）
所以 $∠ C F E = ∠ C M D = 90 °$ （）
所以 $E F ∥ D M$ ，（）
所以 $∠ 2 = ∠ C D M$ ．（）
因为 $∠ 1 = ∠ 2$ ，（已知）
所以 $∠ 1 = ∠$ _▲_，（）
所以 $M N ∥ C D$ ，（）
又因为 $∠ 3 = ∠ C$ （已知）
所以 $A B ∥ C D$ ．（）
所以 $A B ∥ M N$ ．（）

查看试题解析
20. 如图，已知∠A=∠AGE，∠D=∠DGC．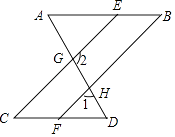

(1)、求证：AB∥CD；

(2)、若∠2+∠1=180°，且∠BEC=2∠B+30°，求∠C的度数．

查看试题解析
21. 如图，在平面直角坐标系中， $A (- 4, - 3)$ ， $B (1, - 1)$ ， $C (- 2, 3)$ ．

(1)、三角形ABC中任意一点 $P (x_{0}, y_{0})$ 经平移后对应点为 $P^{'} (x_{0} + 4, y_{0} + 3)$ ，将三角形ABC作同样的平移得到三角形 $A^{'} B^{'} C^{'}$ ．画出平移后的三角形 $A^{'} B^{'} C^{'}$ ，写出 $A^{'}$ 、 $B^{'}$ 、 $C^{'}$ 的坐标： $A^{'}$ _▲_， $B^{'}$ _▲_， $C^{'}$ _▲_；

(2)、直接写线段BC与x轴交点D的坐标；

(3)、若将线段CB沿水平方向平移一次，再竖直方向平移一次，两次平移扫过的图形没有重叠部分．两次平移后点B的对应点 $B^{″}$ 的坐标为 $(1 + a, - 1 + b)$ ，已知线段CB扫过的面积为20，请直接写出a ， b的数量关系：．

查看试题解析
22.

(1)、如图，计划在空地上设计3块并排的正方形基地做厂房存放生产物资，基地总面积为 $1200 m^{2}$ ，则每块正方形基地的边长为m．

(2)、计划在厂房的东边围一个面积为 $300 m^{2}$ 的长方形基地，做仓库存放设备，仓库一边靠在正方形的边上（计划与厂房共一面墙，且共用部分不超过正方形的边长，不考虑门窗），另外三边用材料围成，并且它的长与宽之比为 $5 : 2$ ．若可以围成，请通过计算设计出方案，并简要画出设计图；若不能围成，请通过计算说明理由．

查看试题解析
23. 问题探究：

(1)、如图1， $A B ∥ C D$ ，点P在直线 $A B$ 上方（ $∠ A E P > ∠ C F P$ ）．
①请在拐点P处作直线 $A B$ 平行∥平行线；
②探究 $∠ A E P$ 、 $∠ C F P$ 、 $∠ E P F$ 之间的数量关系为_▲_．

(2)、问题拓展：如图2， $A B ∥ C D$ ，点P在直线 $A B$ 上方， $∠ A E P$ 的角平分线 $E M$ 所在的直线和 $∠ D F P$ 的角平分线 $F N$ 所在的直线交于点G（点G在直线 $C D$ 的下方），请写出 $∠ E P F$ 和 $∠ E G F$ 之间的数量关系，并证明．

(3)、问题迁移：如图3， $A B ∥ C D$ ，点P在直线 $A B$ 上方， $E G$ 、 $E S$ 、 $F M$ 、 $F T$ 分别是 $∠ A E P$ 、 $∠ B E P$ 、 $∠ C F P$ 、 $∠ D F P$ 的三等分线，且 $\frac{∠ A E G}{∠ A E P} = \frac{∠ P E S}{∠ P E B} = \frac{∠ M F P}{∠ C F P} = \frac{∠ D F T}{∠ D F P} = \frac{2}{3}$ ．直线 $E S$ 与直线 $F M$ 交于点M ，直线 $E G$ 与直线 $F T$ 交于点N（点N在直线 $C D$ 的下方）．设 $∠ E M F - ∠ E N F = α$ ，请直接写出 $α$ 与 $∠ P$ 的数量关系：．

查看试题解析
24. 在平面直角坐标系中，已知点 $A (a, 0)$ ， $B (0, b)$ ， $C (0, - 4)$ ，且a和b满足 ${(a + 4)}^{2} + \sqrt{2 - b} = 0$ ．将线段 $A B$ 平移，使得点A、B分别与点C、D重合．

(1)、请直接写出点A、B、D的坐标：A ， B ， D；

(2)、如图1，若点P为直线AB上一点，将点P向右平移t个单位到点 $P^{'}$ ，当点 $P^{'}$ 在直线 $C D$ 上时，则t的值为_▲_，若三角形 $C O P^{'}$ 的面积是三角形 $D O P^{'}$ 的面积的2倍，请求出点P的坐标；

(3)、如图2，若点 $Q (m, n)$ 为平面直角坐标系内一点，且三角形 $A B Q$ 的面积是三角形 $C D Q$ 的面积的2倍，请探究m ， n的数量关系，并写出你的探究过程．

查看试题解析